HashMap

HashMap이란?

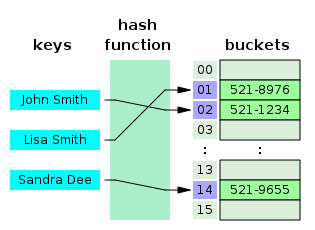
{key, value} 쌍으로 이루어진 값을 저장하며 탐색, 삭제, 저장을 O(1) 으로 수행하는데 목적을 가진 자료구조

저장 및 조회 방식

1. hash함수 를 사용해서 key 를 해쉬 값으로 만듦 = bucket
2. bucket에 실제 데이터인 {key, value} 쌍을 저장
3. 데이터를 조회할 때 key값을 hash함수를 사용해서 해당 bucket의 데이터를 반환

시간 복잡도

Operation	Best Time
store	O(1)
delete	O(1)
search	O(1)

• Collison이 일어나지 않은 경우 모두 O(1)

---

Collision ( 충돌 )

서로 다른 key에 대해 hash함수 의 bucket 이 같은 결과가 나와서 충돌이 일어나 발생하는 문제

Collision 대응책

• open addressing
• separete chaining
• 충돌이 덜 일어나게 좋은 해쉬 함수를 사용하기

1. Open addressing

Collision이 발생하면 특정 로직에 따라 table의 비어있는 bucket을 찾아서 데이터를 저장하는 방식

• Linear Proding( 선형 조사법 )
  Collision이 발생하면 일정 값 만큼 건너 뛰어 빈 bucket에 데이터를 저장 함
  ( bucket + 1, bucket + 2, bucket+3 … )
• Quadratic Proding( 이차 조사법 )
  Collision이 발생하면 제곱수로 건너 뛰어 빈 bucket에 데이터를 저장
  ( bucket + 1^2, bucket + 2^2, bucket+3^2 … )

선형 조사법과 이차조사법의 경우 Collision이 많이 일어 날수록 특정 영역 에 데이터가 몰리는 clustering이 발생함
-> 결국 같은 증가폭으로 탐색을 하기 때문에 충돌이 잦음
( clustering이 발생하면 탐색 시간이 증가하게 됨 )

---

• Double Hashing
  해시함수를 2개를 사용하는 방식
  하나는 buket을 얻는데 사용하고 하나는 충돌이 발생할 경우 이동폭을 얻기 위해 사용 함
  선형 조사법, 이차 조사법 보다 균일하게 분포시킬 수 있음

(hash1(key) + i * hash2(key)) % TABLE_SIZE ( 충돌 발생 시 i 를 증가시켜서 탐색 i 는 1부터 시작 )

• 자주 사용하는 hash1
  hash1(key) = key % TABLE_SIZE
• 자주 사용하는 hash2 ( prime < TABLE_SIZE )
  hash2(key) = prime - ( key % prime )

Dobule Hasing 예제

Table Size = 13이고 Prime은 7일 때

Hash1(key) = key % 13
Hash2(key) = 7 - (key%7) 

key가 36, 10일 경우
Hash1(36) = 10, Hash1(10) = 10 ( 값이 10으로 동일 충돌 발생 !)

충돌해결하기 
1. Hash2(10) = 7 - (10 % 7) = 4
2. Double Hash = (Hash1(10) + 1 * Hash2(10)) % 13 = (10 + 1 * 4) % 13 = 1

1이 나왔지만 Hash1(27)과 Collision이 발생 → i 값을 증가시켜서 충돌 확인

Dobule Hash = (Hash1(10) + 2 * Hash2(10)) % 13 = (10 + 2 * 4) % 13 = 5

5에는 충돌이 없으므로 해결 !

---

2. Separate Chaining

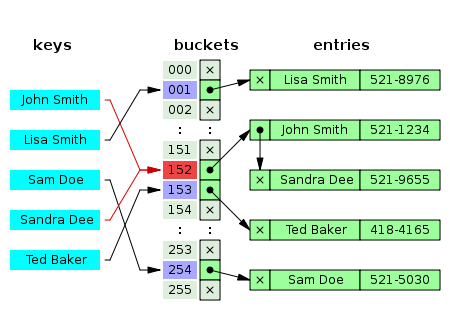
Linked List 혹은 BST를 이용해서 Collison을 해결하는 방식. 충돌이 일어나면 Linked List에 노드를 추가하여 데이터를 연속적이게 저장 함

삽입 삭제 시 bukcet의 키 값이 일치하면 바로 처리하면 되지만 일치하지 않을 경우 Linked List를 순회해야 함

Linked List가 너무 길어져서 느려지는 것을 개선하기 위해 BST에 저장하여 Worst Time을 O(log n)으로 줄이는 방식도 있음

시간 복잡도

Operation	Best Time	Worst Time (Linked List)	Worst Time (BST)
store	O(1)	O(1)	O(log n)
delete	O(1)	O(n)	O(log n)
search	O(1)	O(n)	O(log n)

• Linked List의 장점 : 저장할 때 맨 앞에 저장하고 포인터를 이동하면 되므로 O(1)만에 수행 가능
• BST의 장점 : 정렬된 트리이기 때문에 저장, 탐색, 삭제를O(log n)에 수행 가능

Separate Chaining( Linked List )

struct Node{
    int key, val;
    Node* next;

    Node(int k, int v, Node* node){
        key = k;
        val = v;
        next = node;
    }
};

class MyHashMap {
public:
    static const int size = 19997;
    static const int mul = 12582917;
    Node* map[size] = {};

    int hash(int key){
        return (int)((long long)key * mul % size);
    }
    
    void put(int key, int value) {
        remove(key);
        int idx = hash(key);
        Node* node = new Node(key, value, map[idx]);
        map[idx] = node;
    }
    
    int get(int key) {
        int idx = hash(key);
        Node* node = map[idx];
        while(node != nullptr){
            if(node->key == key){
                return node->val;
            }
            node = node->next;
        }
        return -1;
    }             
    
    void remove(int key) {
        int idx = hash(key);
        Node* node = map[idx];
        if(node == nullptr) return;
        if(node->key == key){
            map[idx] = node->next;
            delete node;
        }
        else{
            while(node->next != nullptr){
                if(node->next->key == key){
                    Node* tmp = node->next;
                    node->next = tmp->next;
                    delete tmp;
                    return;
                }
                node = node->next;
            }
        }
    }
};

/**
 * Your MyHashMap object will be instantiated and called as such:
 * MyHashMap* obj = new MyHashMap();
 * obj->put(key,value);
 * int param_2 = obj->get(key);
 * obj->remove(key);
 */

Separate Chaining (BST)

일반 BST를 구현한 코드로 균형이 깨질 경우 worst time이 O(n)입니다.
추후에 균형을 맞출 수 있는 AVL트리나 Red Black트리를 알아보고 정리하겠습니다.

struct Node
{
    int key, value;
    Node *left, *right;

    Node(int k, int v)
    {
        key = k;
        value = v;
        left = nullptr;
        right = nullptr;
    }
};

class BST
{
public:
    static Node *insertBST(Node *node, Node *newNode)
    {
        if (node == nullptr)
        {
            return newNode;
        }
        if (node->key < newNode->key)
        {
            node->right = insertBST(node->right, newNode);
        }
        else if (node->key > newNode->key)
        {
            node->left = insertBST(node->left, newNode);
        }
        return node;
    }

    static int searchBST(Node *node, int key)
    {
        if (node == nullptr)
            return -1;

        if (node->key < key)
        {
            searchBST(node->right, key);
        }
        else if (node->key > key)
        {
            searchBST(node->left, key);
        }
        else
        {
            return node->value;
        }
        return -1;
    }

    static Node *deleteBST(Node *node, int key)
    {
        if (node == nullptr)
        {
            return node;
        }
        if (node->key < key)
        {
            node->right = deleteBST(node->right, key);
        }
        else if (node->key > key)
        {
            node->left = deleteBST(node->left, key);
        }
        else
        {
            // No child
            if (node->left == nullptr && node->right == nullptr)
            {
                delete node;
                return nullptr;
            }
            // One Child
            if (node->left == nullptr || node->right == nullptr)
            {
                Node *tmp = node->left ? node->left : node->right;
                delete node;
                return tmp;
            }
            // Two Child
            if (node->left && node->right)
            {
                Node *tmp = node->left;
                while (tmp->right)
                {
                    tmp = tmp->right;
                }
                node->key = tmp->key;
                node->value = tmp->value;
                node->left = deleteBST(node->left, key);
            }
        }
        return node;
    }
};

class HashMap
{
    static const int mul = 12582917;
    static const int size = 19997;
    Node *map[size] = {};

public:
    int hash(int key)
    {
        return (int)((long long)key * mul % size);
    }

    void insert(int key, int value)
    {
        remove(key);
        int bucket = hash(key);
        if (map[bucket] == nullptr)
        {
            map[bucket] = new Node(key, value);
        }
        else
        {
            Node *newNode = new Node(key, value);
            map[bucket] = BST::insertBST(map[bucket], newNode);
        }
    }

    int search(int key)
    {
        int bucket = hash(key);
        return BST::searchBST(map[bucket], key);
    }

    void remove(int key)
    {
        int bucket = hash(key);
        BST::deleteBST(map[bucket], key);
    }
};

int main()
{
    HashMap *map = new HashMap();
    map->insert(1, 2);
    map->insert(2, 3);
    map->insert(3, 4);
    map->insert(4, 6);
    map->insert(5, 11);
    map->insert(6, 7);
    map->insert(7, 8);

    cout << map->search(4) << endl;
    cout << map->search(5) << endl;
    cout << map->search(6) << endl;
    cout << map->search(7) << endl;

    cout << endl;
    map->remove(4);
    cout << map->search(4) << endl;
    cout << map->search(5) << endl;
    cout << map->search(6) << endl;
    cout << map->search(7) << endl;
    return 0;
}

Application

• 빠른O(1)시간만에 데이터를 삽입, 삭제, 조회가 필요할 경우 사용