Tree

그래프의 일종으로 한 루트 노드에서 시작해서 자기 자신에게 돌아오지 못하는 순환이 없는 그래프이다.

• root node : 최상위 노드
• leaf node : 자식 노드가 없는 노드
• internal node : leaf node가 아닌 노드 ( 내부 노드 )

Binary Tree

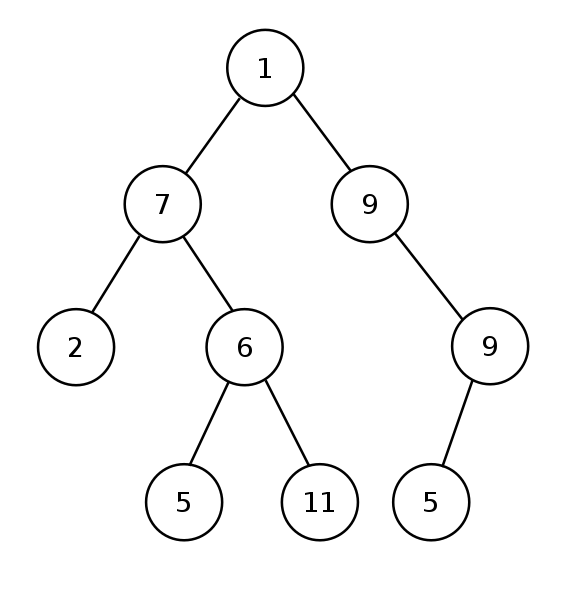
각각의 부모 노드가 최대 2개의 자식 노드를 가질 수 있는 트리

구성 요소

• val ( 데이터 )
• left child
• right child

sturct Node{
	int val;
	Node* left, *right;
};

Binary Tree의 종류

1. Full Binary Tree

모든 부모 노드들이 2개의 자식 노드를 가지거나 가지지 않는 트리

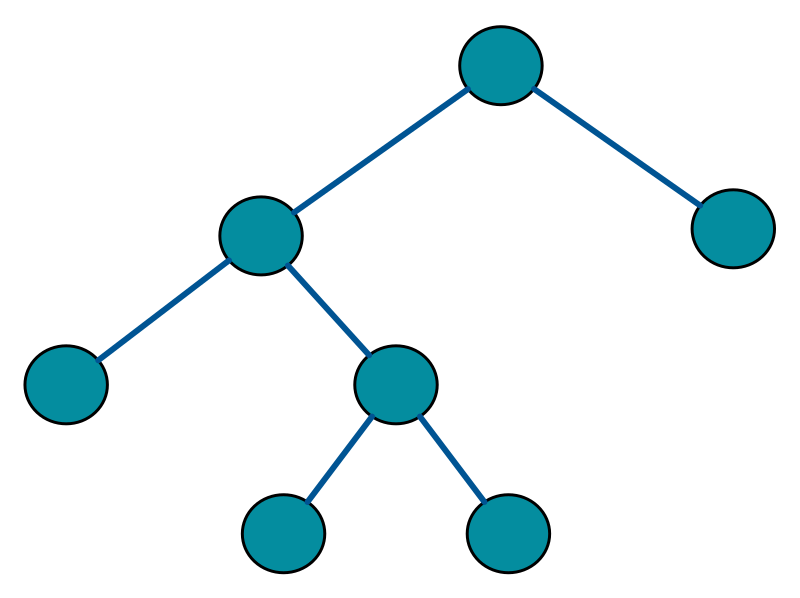
i = the number of internal nodes ( 내부 노드 = 자식을 가진 노드 )
n = be the total number of nodes
l = number of leaves
λ = number of levels

l = i + 1
n = 2i + 1            // i + l = i + (i + 1)

i = (n-1)/2           // (2i + 1 - 1)/2 = i
l = (n+1)/2           // (2i+1+1)/2 = 2i+1

n = 2l-1              // 2(i+1)-1
i = l-1               // i+1-1
(max)l: 2^(λ - 1)    // 최대 leaf개수

Full Binary Tree를 체크하는 예제

struct Node
{
    int key;
    Node *left, *right;

    Node(int k)
    {
        key = k;
    }
};

bool isFullBinaryTree(Node *root)
{
    if (root == nullptr)
    {
        return true;
    }
    if (root->left == nullptr && root->right == nullptr)
    {
        return true;
    }
    if (root->left && root->right)
    {
        return isFullBinaryTree(root->left) && isFullBinaryTree(root->right);
    }
    return false;
}

int main()
{
    Node *root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->left->right->left = new Node(6);
    root->left->right->right = new Node(7);

    if (isFullBinaryTree(root))
    {
        cout << "Is Full Binary Tree" << endl;
    }
    else
    {
        cout << "Is not Full Binary Tree" << endl;
    }

    return 0;
}

2. Complete Binary Tree

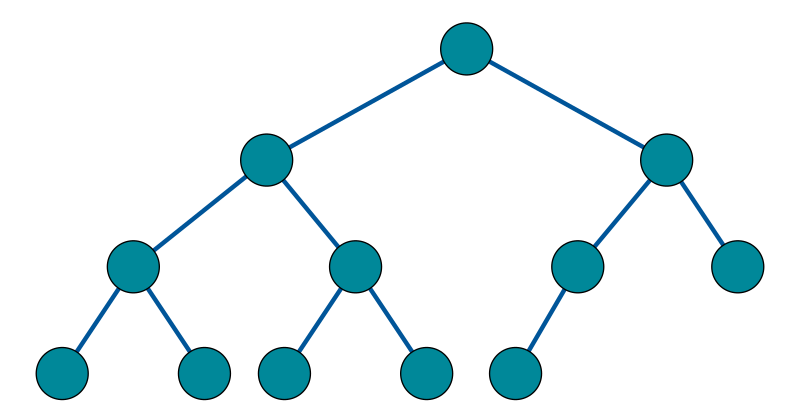
Full Binary Tree와 비슷하지만 차이점이 있음

1. 모든 레벨들이 채워져있어야 함
2. leaf 요소들이 왼쪽으로 치우쳐야 함
3. 마지막 leaf 요소는 Full Binary가 아니여도 됨 ( 0개 혹은 1개의 자식만 있어도 됨 )

left child  = 2i + 1
right child = 2i + 2
parent node = (i-1) / 2

iternal range = [0, n/2 - 1]
leaf range    = [n / 2, n - 1]

Complete Binary Tree 체크하는 예제

struct Node
{
    int key;
    Node *left, *right;

    Node(int key)
    {
        this->key = key;
        this->left = nullptr;
        this->right = nullptr;
    }
};

int getTotalCount(Node *root)
{
    if (root == nullptr)
        return 0;
    return 1 + getTotalCount(root->left) + getTotalCount(root->right);
}

bool checkCompleteTree(Node *root, int idx, int total)
{
    if (root == nullptr)
    {
        return true;
    }
    if (idx >= total)
    {
			// nullptr이아니고(노드가 존재하고) idx가 total 을 넘어서면 complete tree가 아니다.
        return false; 
    }
    return checkCompleteTree(root->left, 2 * idx + 1, total) && checkCompleteTree(root->right, 2 * idx + 2, total);
}

int main()
{
    Node *root = new Node(1);
    root->left = new Node(2);
    // root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);

    int total = getTotalCount(root);
    if (checkCompleteTree(root, 0, total))
    {
        cout << "Complete Tree" << endl;
    }
    else
    {
        cout << "Is not complet tree" << endl;
    }
}

Complete Binary Tree Applications

• Heap-based data structures
• Heap sort

3. Balanced Binary Tree

노드의 왼쪽 트리와 오른쪽 트리의 높이 차이가 0혹은 1인 트리

Balanced Binary Tree 체크하는 예제

class Solution {
public:
		int dfsHeight (TreeNode *root) {
        if (root == NULL) return 0;
        
        int leftHeight = dfsHeight (root -> left);
        if (leftHeight == -1) return -1;
        int rightHeight = dfsHeight (root -> right);
        if (rightHeight == -1) return -1;
        
        if (abs(leftHeight - rightHeight) > 1)  return -1;
        return 1 + max(leftHeight, rightHeight);
    }
    bool isBalanced(TreeNode *root) {
        return dfsHeight (root) != -1;
    }
};