Heap, Heap Sort

Heap

Heap은 Complete Binary Tree이며 Heap 속성을 만족하는 것

Heap 속성

1. Max heap property : 부모 노드의 값이 자식 노드들의 값 보다 큰 속성

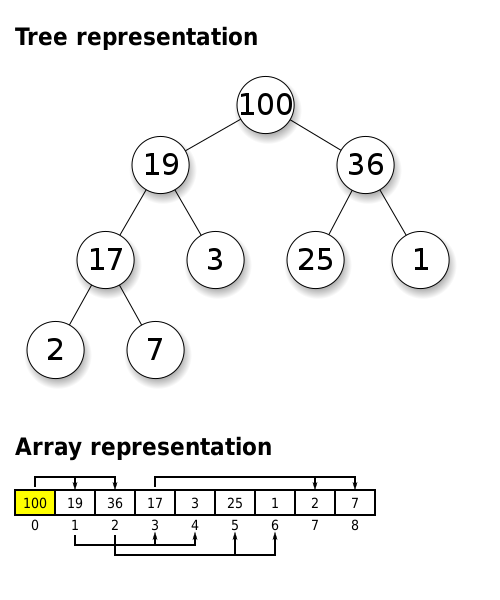
2. Min heap property : 부모 노드의 값이 자식 노드들의 값 보다 작은 속성

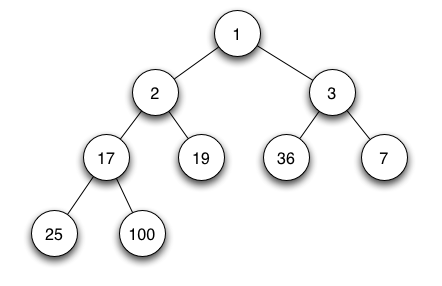
Heapify

binary tree에서 최대 heap을 만드는 과정

1. 주어진 배열로부터 Complete binary tree를 만듦
2. internal 노드의 마지막 index부터 시작 i = (n/2 - 1)
(intenal node index 범위 : [0, n/2 - 1], leaf node index범위 : [n/2, n-1]
4. internal node i와 child node 2i+1, 2i+2를 비교 -> child node가 더 크다면 스왑
5. 스왑을 했다면 다시 child node와 비교해서 반복
6. 모든 internal 노드 범위에서 과정을 반복해서 힙을 만듦
internal node범위에서만 수행하는 이유 : leaf node는 child node가 없으므로 스왑할 일이 없음

Insert Element into Heap

1. 트리의 마지막에 값을 집어넣음
2. Heapify를 수행해서 정렬

Delete Element from Heap

1. 제거될 요소의 index 구하기
2. 마지막 노드와 스왑
3. 마지막 노드 제거
4. Heapify를 수행해서 정렬

// Max-Heap data structure in C++
void heapify(vector<int> &hT, int i)
{
  int size = hT.size();
  int largest = i;
  int l = 2 * i + 1; // 왼쪽 자식 index
  int r = 2 * i + 2; // 오른쪽 자식 index
  if (l < size && hT[l] > hT[largest])
    largest = l;
  if (r < size && hT[r] > hT[largest])
    largest = r;

  if (largest != i) 
  {
    swap(hT[i], hT[largest]); // 부모보다 자식이 더 큰 값이므로 스왑
    heapify(hT, largest); // 스왑된 위치로부터 다시 hepify 수행
  }
}

void insert(vector<int> &hT, int newNum)
{
  int size = hT.size();
  if (size == 0)
  {
    hT.push_back(newNum); // 트리가 비어 있다면 그냥 값을 집어 넣음
  }
  else
  {
    hT.push_back(newNum); // 트리에 마지막에 값을 집어넣고
    for (int i = size / 2 - 1; i >= 0; i--)
    {
      heapify(hT, i); // internal node 범위에서 heapify 수행
    }
  }
}

void deleteNode(vector<int> &hT, int num)
{
  int size = hT.size();
  int i;
  for (i = 0; i < size; i++) // 제거될 node의 index구하기
  {
    if (num == hT[i])
      break;
  }
  swap(hT[i], hT[size - 1]); // 제거될 node와 마지막 node 스왑

  hT.pop_back(); // 마지막 node(스왑 되어서 제거할 node) 제거
  for (int i = size / 2 - 1; i >= 0; i--)
  {
    heapify(hT, i); // internal node에 대해 heapify 수행
  }
}

void printArray(vector<int> &hT)
{
  for (int i = 0; i < hT.size(); ++i)
    cout << hT[i] << " ";
  cout << "\n";
}

int main()
{
  vector<int> heapTree;

  insert(heapTree, 3);
  insert(heapTree, 4);
  insert(heapTree, 9);
  insert(heapTree, 5);
  insert(heapTree, 2);

  cout << "Max-Heap array: ";
  printArray(heapTree);

  deleteNode(heapTree, 4);

  cout << "After deleting an element: ";

  printArray(heapTree);
}

Heap Data Structure Applications

• Dijkstra's Algorithm ( Heap is used while implementing a priority queue )
• Heap Sort

Heap Sort

1. 먼저 배열을 최대 힙으로 만듦 ( root노드가 가장 큰 요소임을 알고 있음 )
2. root 노드와 마지막 노드를 스왑
3. 배열의 사이즈를 1개 줄여서 마지막 노드를 제거 ( 가장 큰 요소 )
4. Heapify 수행
   사이즈가 0이 될때까지 반복 ( 실제 사이즈를 줄이는 것은 아니고 index만 줄여서 정렬되지 않는 node의 위치로 이동하는 것 )

시간 복잡도

Best	O(nlog n)
Worst	O(nlog n)
Average	O(nlog n)
Space Complexity	O(1)

Heap sort는 best, average, worst 모두 O(nlong n) 이다.

⇒ complete binary tree의 높이는 log n 이다.
최악의 경우 : 루트 노드를 leaf 노드까지 스왑해야함 높이인 log n의 시간이 듦

최대힙을 만드는 과정에서 n/2 개의 요소에 최악의 경우 n/2 * log n ~ nlogn 의 시간이 듦

정렬 과정에서 루트 노드와 마지막 노드를 스왑하고 heapify를 함 → 마찬가지 최악의 경우 log n 시간이 듦 n 번 수행하므로 nlogn

최대힙을 만드는것과 정렬하는 것은 개별적으로 수행하므로 곱하지않고 더하기때문에 nlogn 이 됨

별도의 추가 공간은 사용하지 않으므로 공간 복잡도는 O(1)

void heapify(vector<int> &hT, int n, int i)
{
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    int largest = i;

    if (l < n && hT[largest] < hT[l])
    {
        largest = l;
    }
    if (r < n && hT[largest] < hT[r])
    {
        largest = r;
    }

    if (i != largest)
    {
        swap(hT[i], hT[largest]);
        heapify(hT, n, largest);
    }
}

void heapSort(vector<int> &hT)
{
    int n = hT.size();
    for (int i = n / 2 - 1; i >= 0; i--) // heapify 최대 힙 만드는 과정 
    {
        heapify(hT, n, i);
    }
    for (int size = n - 1; size >= 0; size--) // heapsort 과정
    {
        swap(hT[0], hT[size]); // 0번째(가장 큰node)와 마지막 node 스왑
        heapify(hT, size, 0);  // 스왑된 위치(마지막 node)로 부터 heapify 수행
    }
}

int main()
{
    vector<int> hT = {124,
                      312,
                      124123,
                      124321,
                      2324234};
    heapSort(hT);
    for (auto num : hT)
    {
        cout << num << ", ";
    }
    cout << endl;
    return 0;
}