[AI Math] 벡터와 행렬

벡터의 덧셈과 뺄셈

두 벡터의 덧셈과 뺄셈은 다른 벡터로부터 상대적 위치이동을 표현

성분곱(hadamard product)

차원이 같은 두 벡터의 성분(element)를 곱하는 연산

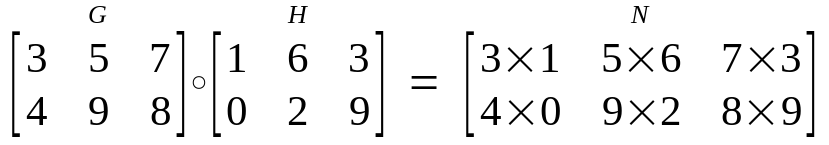
numpy 에서는 *기호로 그대로 사용 가능

벡터의 노름(norm)

• 원점에서부터의 거리

L1 노름 : 각 성분의 변화량의 절대값
L2 노름 : 유클리드 거리
👉 머신러닝에서 각 성질들이 필요할 때가 있으므로 둘 다 사용

두 벡터 사이의 각도

• L2 노름에서만 가능
• 제2 코사인 법칙 이용
• 분자 부분이 두 벡터의 내적

np.inner(x,y)

행렬

• 벡터를 원소로 가지는 2차원 배열
• 벡터공간에서 사용되는 연산자
• 덧셈, 뺄셈, 성분곱, 스칼라곱 같음

행렬의 곱셈

• 행벡터와 열벡터의 내적
  numpy : X @ Y

행렬의 내적

• 수학에서의 내적과 다름
• 행벡터와 행백터의 내적

np.inner(X,Y)

역행렬

np.linalg.inv(X)

무어-펜로즈 역행렬
: 행과 열 숫자가 달라도 계산할 수 있음
$A^{+} = (A^{T}A)^{-1}A^{T}$ (n≥m)
$A^{+} = A^{T}(AA^{T})^{-1}$ (n≤m)

np.linalg.pinv(X)

응용 → 연립방정식, 선형회귀분석 등

[부스트캠프 AI Tech] Week 1 - Day 4