
Session Review
T-Test의 기본 전제조건 (NID)
전제 조건이 맞지 않을 경우 다른 검정방법 사용해야 함 e.g. Chi-square etc
전제조건이 필요한 이유: 평균에 대한 추론을 수행할 때, 조건들을 만족할 때 계산이 정확해지고 결론에 대한 신뢰성이 높아짐
- 정규성 (Normality)
독립변수에 따른 종속변수는 정규분포를 만족해야 함
Why❓ 모집단이 정규분포를 따른다면 여기서 추출한 sample 역시 정규분포를 따름
BUT, 우리는 실제 모집단 분포의 형태를 확인할 수 없기 때문에 표본에서의 자료를 바탕으로 형태를 추론함
-
독립성 (Independent)
독립변수의 그룹 군은 서로 독립적이어야 함
Why❓ 독립변수들이 서로 종속적이면, 각 변수와 종속변수 간의 관계를 파악하기 어려움 -> 통계 데이터 분석이 의미가 없어질 수 있음 -
등분산성 (Distributed with mean of zero and common variance)
독립변수에 따른 종속변수 분포의 분산은 각 군마다 동일해야 함
분산: 통계에서 변량이 평균으로부터 떨어져 있는 정도"같은 모집단에서 나왔는가"를 판단
편향된 표본은 부정확한 결과로 이어지므로, 신뢰구간 형성이나 유의성 검정 시행 어려움
scipy.stats의normaltest를 통해 검증
Type of Error
-
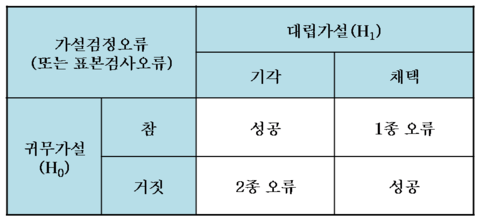
1종 오류
잘못된 부적정 의견을 표명하는 오류 (과소신뢰의 오류)
= 기각(Rejection)의 오류 -> 귀무가설이 참인데 기각하고 대립가설 채택
e.g. 스팸메일이 아닌데 스팸메일로 판단 -
2종 오류
잘못된 적정 의견을 표명하는 오류 (과대신뢰의 오류)
= 채택(Acceptance)의 오류 -> 귀무가설이 거짓인데 채택하고 대립가설 기각
e.g. 암환자를 건강한 환자로 판단
Chi-Square Test
T-test가 표본집단의 평균을 비교할 때 선택하는 방법이라면, chi-square test는 categorical data로 구성된 표본집단의 분포를 비교할 때 선택하는 방법
Categorical data(범주형 데이터): 자료를 '분류'로 묶어서 표현 -> 연속성이 없음
e.g. 1등급, 2등급, 3등급도 연속성이 없는 것
<-> Continuous data(연속형 데이터)
sample의 개수에 따라 one-sample, two-sample로 나뉨
One-sample chi test
Null Hypothesis: Distribution is similar (or specific input)
Alter. Hypothesis: Distribution is not similar (or specific input)
데이터의 분포(Obs)가 특정 예상되는 분포(Exp)와 같은지 확인할 때 사용
Exp = sum(Obs) / count
-> 계산된 카이제곱 통계치를 표준화된 값인 P-value로 바꾸는 과정 필요
stats.chi2.cdf(카이제곱 통계치, df)
분포가 비슷하다는 것 = 두 분포가 보이기에만 다를뿐 사실 같은 분포에서 왔다는 뜻
-> 대립가설 채택하는 경우, 두 분포가 다른 모집단에서 왔을수도 있음을 나타냄 (obs와 exp의 차이는 누구나 생길 수 있는 우연이 아니라 유의미한 차이)
Two-sample chi test
Null Hypothesis: Variable is independent
Alter. Hypothesis: Variable is not independent (or specific input)
chi2_contingency(obs, correction=False)
❗️ independent한 것이 왜 중요할까?
앞서 T-test의 전제조건에서도 언급했다시피, 변수들이 종속적인 경우 그 관계를 파악하기 어려워지고 결과적으로 데이터 분석이 의미가 없어질 수 있기 때문 -> 연관성이 있는지 없는지를 파악하는 것이 중요함
Degrees of Freedom
자유도 = 해당 parameter를 결정짓기 위한 독립적으로 정해질 수 있는 값의 수
= 독립변수의 개수
e.g. 아이스크림 선택
전체 메뉴가 7개라고 가정할 때,
- 월: 7개의 선택지 중 1개 선택
- 화: 6개의 선택지 중 1개 선택
- 수: 5개의 선택지 중 1개 선택
- 목: 4개의 선택지 중 1개 선택
- 금: 3개의 선택지 중 1개 선택
- 토: 2개의 선택지 중 1개 선택
- 일: 선택지 없음🥲 (자유도 X)
이 경우 자유도는 n - 1 = 6
1-sample (적합도 검정), DF = num of categories - 1
2-sample (독립성 검정), DF = (num of row - 1)*(num of column - 1)
food for thought
❓ 가설검정을 써야 하는 이유?
❓ T-Test와 Chi Square Test는 각각 평균과 분포를 비교하는 것 -> 평균과 분포를 비교하는 것이 어떤 의미?
