11월 13일 - 같은 탑[BOJ/1126]

---

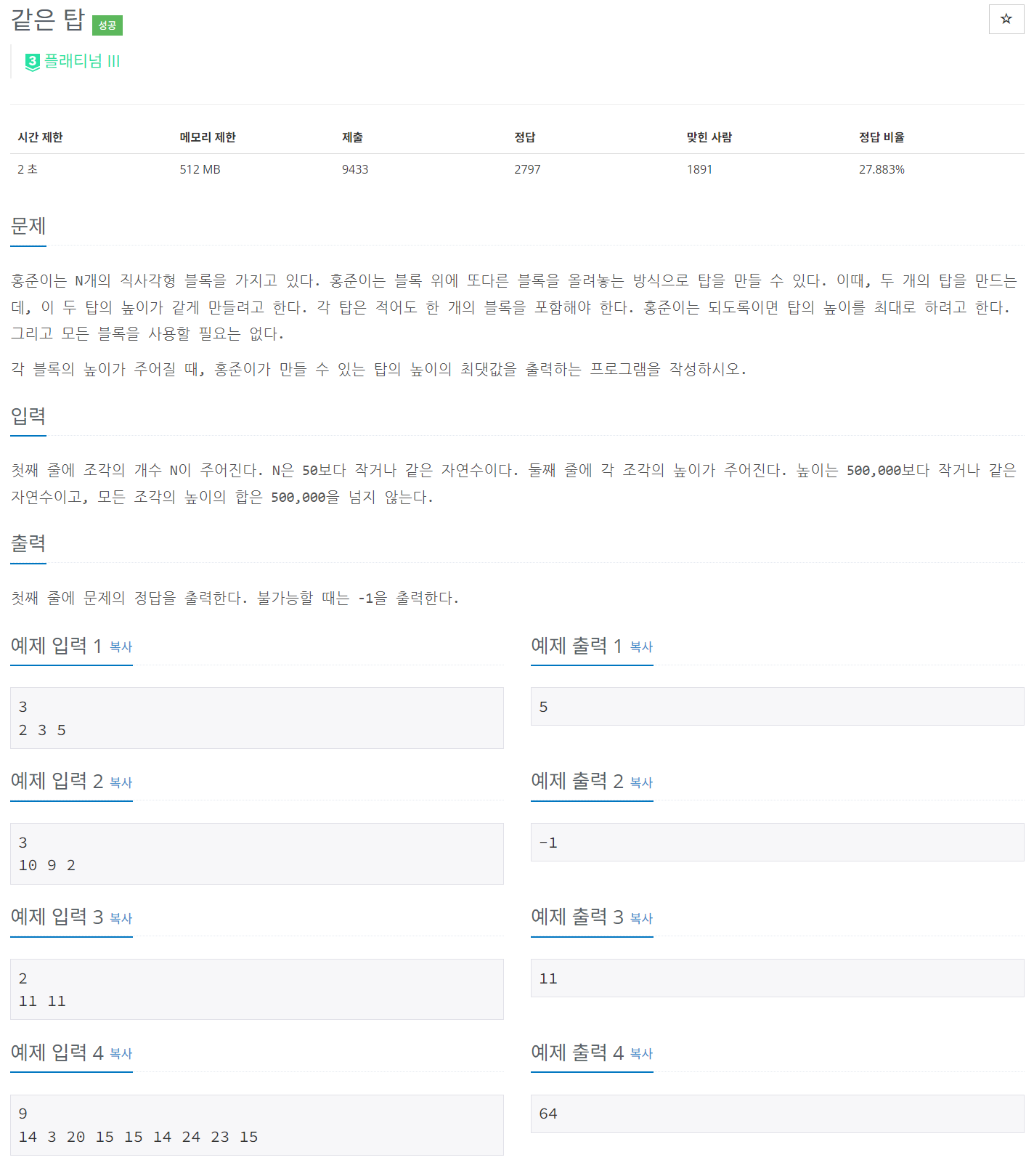
N개의 직사각형 블록으로 두 개의 탑을 만들되, 두 탑의 높이를 같게 하면서 가능한 최대 높이를 구하는 문제를 풀어봤다. 이 문제는 각 블록의 높이를 합쳐서 특정 높이의 차이를 최소화하는 방식으로 접근할 수 있다. 동적 계획법(DP)을 사용해 부분합의 차이를 조절하는 방식으로 풀이했다.

문제 접근 방법

1. 동적 계획법(DP) 설계:

• dp[i][d]는 i번째 블록까지 고려했을 때 두 탑의 높이 차이가 d일 때의 최대 높이를 저장한다.
• 두 탑의 높이를 맞추려면, 결국 두 탑의 높이 차이(d)가 0이 되는 순간의 최대 높이를 찾아야 한다.
• 모든 블록을 선택하지 않아도 되므로 각 블록을 사용하거나 사용하지 않는 경우를 고려하여 가능한 모든 높이 차이를 탐색한다.

2. 상태 전이 정의:

• 세 가지 선택지가 있다:
  1. 현재 블록을 사용하지 않고 넘어가는 경우.
  2. 현재 블록을 더 높은 탑에 추가하는 경우.
  3. 현재 블록을 더 낮은 탑에 추가하는 경우.
• 이 중 최대 높이를 선택하여 DP 배열에 저장한다.

3. 결과 판별:

• 최종적으로 dp[N][0]이 0보다 크면 그 값을 출력하고, 아니면 -1을 출력해 두 탑의 높이를 맞추는 것이 불가능하다는 것을 나타낸다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    static int[] blocks;
    static int[][] dp;
    static int N;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        
        // 블록의 개수 입력
        N = Integer.parseInt(br.readLine());
        blocks = new int[N];

        // 블록 높이 입력
        StringTokenizer st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++) {
            blocks[i] = Integer.parseInt(st.nextToken());
        }

        // dp 배열 초기화
        dp = new int[N + 1][500001];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }

        int answer = findMaxHeight(0, 0);
        System.out.println(answer > 0 ? answer : -1);
    }

    // 다이나믹 프로그래밍을 통해 최대 탑 높이 계산
    static int findMaxHeight(int index, int diff) {
        if (index == N) {
            return (diff == 0) ? 0 : Integer.MIN_VALUE;
        }

        if (dp[index][diff] != -1) {
            return dp[index][diff];
        }

        int skip = findMaxHeight(index + 1, diff); // 현재 블록을 사용하지 않는 경우
        int addToTaller = findMaxHeight(index + 1, diff + blocks[index]) + blocks[index]; // 더 높은 탑에 현재 블록 추가
        int addToShorter = findMaxHeight(index + 1, Math.abs(diff - blocks[index])) + (diff > blocks[index] ? 0 : blocks[index] - diff); // 더 낮은 탑에 현재 블록 추가

        dp[index][diff] = Math.max(skip, Math.max(addToTaller, addToShorter));
        return dp[index][diff];
    }
}

코드 설명

1. 입력 처리 및 초기화:

N = Integer.parseInt(br.readLine());
blocks = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
    blocks[i] = Integer.parseInt(st.nextToken());
}
dp = new int[N + 1][500001];
for (int[] row : dp) {
    Arrays.fill(row, -1);
}

• 블록의 개수를 입력받고, 각 블록의 높이를 배열에 저장한다.
• dp 배열을 -1로 초기화하여 아직 계산되지 않은 상태를 표시한다.

2. 탑의 최대 높이를 찾는 재귀 함수 findMaxHeight:

static int findMaxHeight(int index, int diff) {
    if (index == N) {
        return (diff == 0) ? 0 : Integer.MIN_VALUE;
    }
    if (dp[index][diff] != -1) {
        return dp[index][diff];
    }

• findMaxHeight는 index 번째 블록까지 고려했을 때, 두 탑의 높이 차이가 diff일 때의 최대 높이를 반환한다.
• index가 N에 도달했을 때 diff가 0이면 두 탑이 같은 높이인 경우이므로 0을 반환한다. 그렇지 않다면 불가능한 경우이므로 Integer.MIN_VALUE를 반환한다.
• 이미 계산된 값이 있는 경우(dp[index][diff] != -1) 저장된 값을 반환해 중복 계산을 피한다.

3. 세 가지 선택지에 따른 최대 높이 계산:

코드 복사
int skip = findMaxHeight(index + 1, diff); // 현재 블록을 사용하지 않는 경우
int addToTaller = findMaxHeight(index + 1, diff + blocks[index]) + blocks[index]; // 더 높은 탑에 현재 블록 추가
int addToShorter = findMaxHeight(index + 1, Math.abs(diff - blocks[index])) + (diff > blocks[index] ? 0 : blocks[index] - diff); // 더 낮은 탑에 현재 블록 추가

• 블록 사용하지 않기: skip은 현재 블록을 사용하지 않고 다음 블록으로 넘어가는 경우이다.
• 더 높은 탑에 추가: addToTaller는 현재 블록을 더 높은 탑에 추가하는 경우로, 높이 차이가 diff + blocks[index]로 증가한다.
• 더 낮은 탑에 추가: addToShorter는 현재 블록을 더 낮은 탑에 추가하는 경우로, 높이 차이가 Math.abs(diff - blocks[index])로 변화한다.

4. 현재 상태의 최대 높이 저장 및 반환:

코드 복사
dp[index][diff] = Math.max(skip, Math.max(addToTaller, addToShorter));
return dp[index][diff];

• 세 가지 선택 중 최대 높이를 dp[index][diff]에 저장하여 나중에 재사용하고, 그 값을 반환한다.

5. 최종 결과 출력:

코드 복사
int answer = findMaxHeight(0, 0);
System.out.println(answer > 0 ? answer : -1);

• findMaxHeight(0, 0)을 호출하여 두 탑의 높이 차이가 0이 되면서 최대 높이가 되는 값을 구하고, 그 값이 양수면 출력하고, 그렇지 않으면 -1을 출력한다.

So...

이 문제는 DP를 활용해 모든 블록을 선택하거나 선택하지 않으면서 두 탑의 높이를 맞추는 문제였다. 특히, 두 탑의 높이 차이를 상태로 유지하면서 각 블록을 배치하는 방법으로 최적해를 구했다.