11월12일 - 수열과 쿼리22[BOJ/16978]

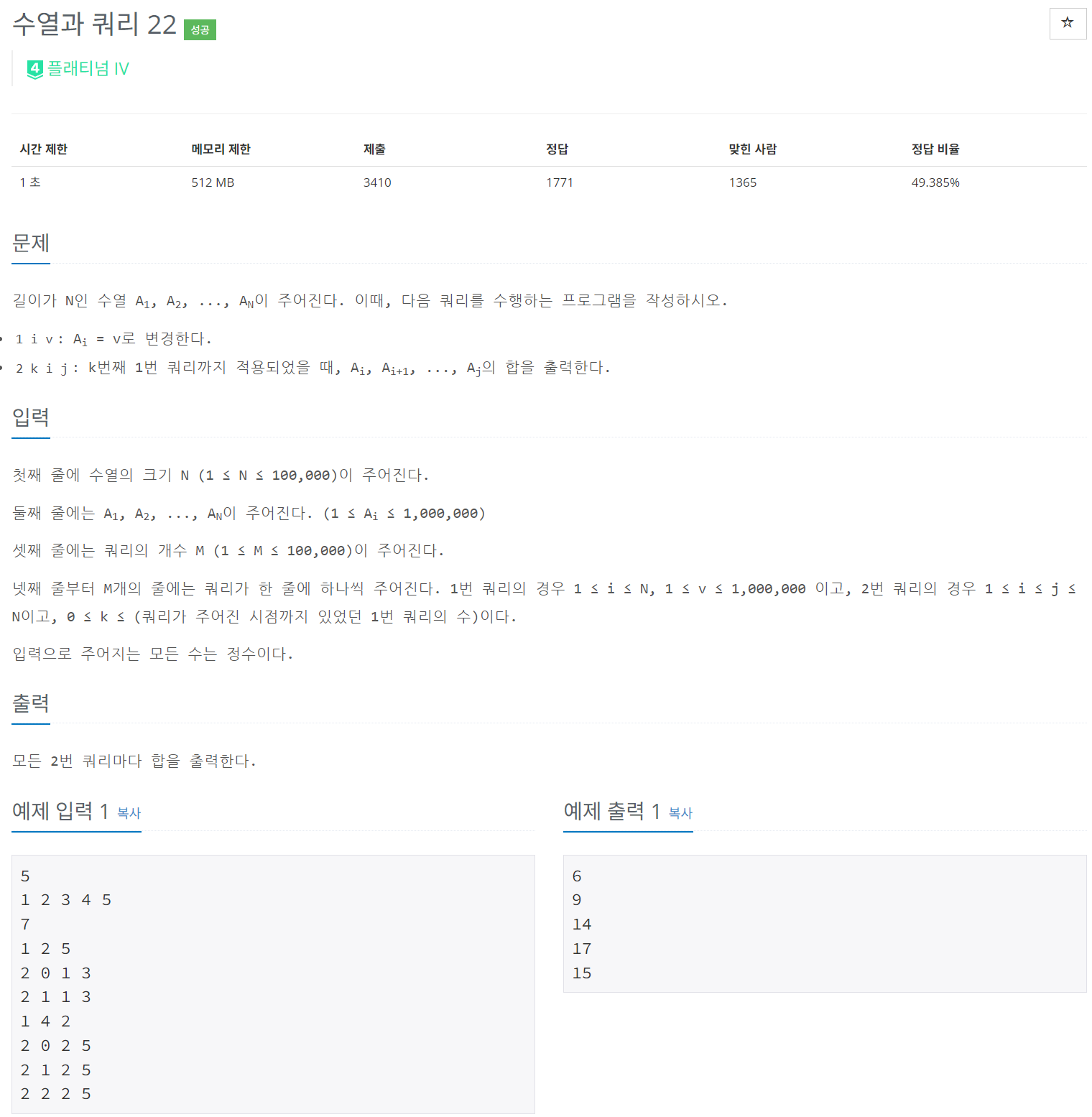
수열의 값들을 업데이트하면서 구간 합을 구하는 문제를 풀어봤다. 이 문제는 수열의 크기와 쿼리의 개수가 최대 100,000에 이르기 때문에 세그먼트 트리를 이용한 효율적인 접근이 필요했다. 특히, 과거 특정 시점까지 적용된 업데이트 상태에서 구간 합을 구하는 쿼리가 있기 때문에, 쿼리를 정렬하고 순차적으로 업데이트를 적용하는 방식으로 해결했다.

문제 접근 방법

1. 세그먼트 트리를 사용한 구간 합 및 업데이트:

• 세그먼트 트리는 구간 합을 빠르게 계산하고 업데이트할 수 있는 자료구조로, O(log N)의 시간 복잡도로 업데이트와 구간 합을 처리할 수 있다.
• 수열의 값들이 주어지면 세그먼트 트리를 초기화하고, 각 업데이트와 구간 합 쿼리를 효율적으로 처리할 수 있게 설계했다.

2. 업데이트와 구간 합 쿼리 분리:

• 1 i v 형태의 쿼리는 특정 인덱스의 값을 변경하는 업데이트 쿼리다. 이러한 쿼리들을 리스트에 저장해두고, 필요한 시점에 적용했다.
• 2 k i j 형태의 쿼리는 k번째 1번 쿼리까지 적용했을 때의 구간 합을 구하는 쿼리로, 구간 합 쿼리 리스트에 저장하고 k 값에 따라 정렬해 순차적으로 처리했다.

3. 정렬과 순차 처리:

• 구간 합 쿼리를 k 값 기준으로 정렬한 후, 필요한 만큼만 업데이트를 반영하며 구간 합을 계산했다. 이를 통해 중복 업데이트를 방지하고 효율적으로 결과를 구할 수 있었다.

Code

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static long[] segTree;
    static long[] result;
    static int N;
    static final int MAX = 100000;

    static class Query {
        int k, start, end, index;
        public Query(int k, int start, int end, int index) {
            this.k = k;
            this.start = start;
            this.end = end;
            this.index = index;
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        
        // 수열의 크기와 수열 입력 처리
        N = Integer.parseInt(br.readLine());
        segTree = new long[4 * N];
        StringTokenizer st = new StringTokenizer(br.readLine());
        
        for (int i = 1; i <= N; i++) {
            int value = Integer.parseInt(st.nextToken());
            updateSegTree(1, 1, N, i, value);
        }

        // 쿼리 개수와 쿼리 처리 준비
        int M = Integer.parseInt(br.readLine());
        List<int[]> updates = new ArrayList<>();
        List<Query> queries = new ArrayList<>();
        result = new long[M];
        int queryIndex = 0;

        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int type = Integer.parseInt(st.nextToken());

            if (type == 1) {
                int index = Integer.parseInt(st.nextToken());
                int value = Integer.parseInt(st.nextToken());
                updates.add(new int[]{index, value});
            } else {
                int k = Integer.parseInt(st.nextToken());
                int start = Integer.parseInt(st.nextToken());
                int end = Integer.parseInt(st.nextToken());
                queries.add(new Query(k, start, end, queryIndex++));
            }
        }

        // 쿼리를 k에 따라 정렬하여 처리
        queries.sort(Comparator.comparingInt(q -> q.k));
        
        int updateIndex = 0;
        for (Query query : queries) {
            // 필요한 업데이트 쿼리를 모두 반영
            while (updateIndex < query.k) {
                int[] update = updates.get(updateIndex++);
                int index = update[0];
                int value = update[1];

                // 현재 index에 있는 값과 새로운 값의 차이를 구하고 적용
                long currentValue = querySegTree(1, 1, N, index, index);
                long diff = value - currentValue;
                updateSegTree(1, 1, N, index, diff);
            }

            // 구간 합 쿼리 수행 및 결과 저장
            result[query.index] = querySegTree(1, 1, N, query.start, query.end);
        }

        // 결과 출력
        StringBuilder output = new StringBuilder();
        for (int i = 0; i < queryIndex; i++) {
            output.append(result[i]).append("\n");
        }
        System.out.print(output);
    }

    // 세그먼트 트리 업데이트
    static void updateSegTree(int node, int start, int end, int index, long diff) {
        if (index < start || index > end) {
            return;
        }
        segTree[node] += diff;
        if (start != end) {
            int mid = (start + end) / 2;
            updateSegTree(node * 2, start, mid, index, diff);
            updateSegTree(node * 2 + 1, mid + 1, end, index, diff);
        }
    }

    // 세그먼트 트리 구간 합 쿼리
    static long querySegTree(int node, int start, int end, int left, int right) {
        if (right < start || end < left) {
            return 0;
        }
        if (left <= start && end <= right) {
            return segTree[node];
        }
        int mid = (start + end) / 2;
        return querySegTree(node * 2, start, mid, left, right) + 
               querySegTree(node * 2 + 1, mid + 1, end, left, right);
    }
}

코드설명

1. 쿼리 클래스 생성:

static class Query {
    int k, start, end, index;
    public Query(int k, int start, int end, int index) {
        this.k = k;
        this.start = start;
        this.end = end;
        this.index = index;
    }
}

• 구간 합 쿼리를 나타내는 Query 클래스를 정의했다.
• k는 몇 번째 업데이트까지 적용할 것인지, start와 end는 구간의 시작과 끝 인덱스를 나타낸다.

2. 세그먼트 트리 초기화:

for (int i = 1; i <= N; i++) {
    int value = Integer.parseInt(st.nextToken());
    updateSegTree(1, 1, N, i, value);
}

• 초기 수열 값을 세그먼트 트리에 넣어 초기화했다.

3. 업데이트와 쿼리 입력 처리:

for (int i = 0; i < M; i++) {
    st = new StringTokenizer(br.readLine());
    int type = Integer.parseInt(st.nextToken());

    if (type == 1) {
        int index = Integer.parseInt(st.nextToken());
        int value = Integer.parseInt(st.nextToken());
        updates.add(new int[]{index, value});
    } else {
        int k = Integer.parseInt(st.nextToken());
        int start = Integer.parseInt(st.nextToken());
        int end = Integer.parseInt(st.nextToken());
        queries.add(new Query(k, start, end, queryIndex++));
    }
}

• 1번 쿼리는 업데이트 리스트에, 2번 쿼리는 구간 합 쿼리 리스트에 추가했다.

4. 쿼리 처리 및 구간 합 쿼리 수행:

int updateIndex = 0;
for (Query query : queries) {
    while (updateIndex < query.k) {
        int[] update = updates.get(updateIndex++);
        int index = update[0];
        int value = update[1];
        long currentValue = querySegTree(1, 1, N, index, index);
        long diff = value - currentValue;
        updateSegTree(1, 1, N, index, diff);
    }
    result[query.index] = querySegTree(1, 1, N, query.start, query.end);
}

• k 값에 따라 필요한 만큼만 업데이트를 반영하고, 구간 합 쿼리를 수행했다.

5. 세그먼트 트리 업데이트 및 구간 합 함수:

static void updateSegTree(int node, int start, int end, int index, long diff) {
    if (index < start || index > end) return;
    segTree[node] += diff;
    if (start != end) {
        int mid = (start + end) / 2;
        updateSegTree(node * 2, start, mid, index, diff);
        updateSegTree(node * 2 + 1, mid + 1, end, index, diff);
    }
}

static long querySegTree(int node, int start, int end, int left, int right) {
    if (right < start || end < left) return 0;
    if (left <= start && end <= right) return segTree[node];
    int mid = (start + end) / 2;
    return querySegTree(node * 2, start, mid, left, right) + 
           querySegTree(node * 2 + 1, mid + 1, end, left, right);
}

• updateSegTree는 세그먼트 트리에서 특정 인덱스를 업데이트하는 함수다.
• querySegTree는 특정 구간의 합을 구하는 함수다.

So...

세그먼트 트리와 K 번째 업데이트만 적용하는 방식으로, 대량의 업데이트와 구간 합을 효율적으로 처리할 수 있었다. 쿼리를 k 값 기준으로 정렬하고 필요한 만큼만 업데이트를 적용함으로써 시간 복잡도를 최적화했다.