11월 1일 - Banks[10350/BOJ]

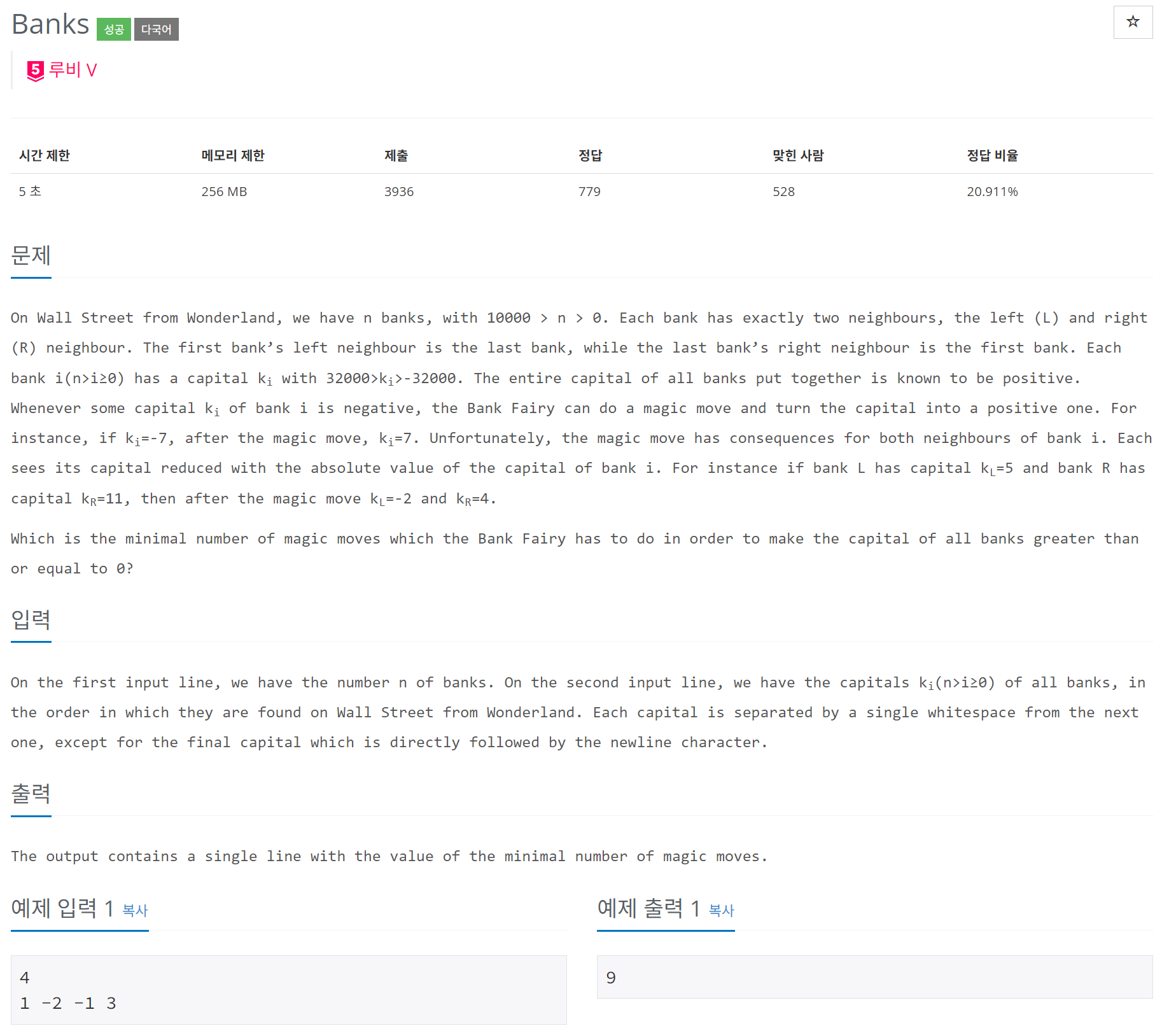
주어진 자본을 양수로 만들기 위해 최소한의 마법 이동 횟수를 계산하는 문제를 풀어봤다. 문제에서 은행들이 원형으로 연결된 구조라는 점과, 각 은행의 자본이 음수일 경우 이를 양수로 만들고, 이로 인해 인접한 은행들이 영향을 받는다는 것이 핵심이다. 문제 해결에 있어 순환형 배열을 효과적으로 활용하는 방법이 주요 과제였다.

문제 접근 방법

1. 순환형 배열 설정: 주어진 은행 리스트가 순환형 구조이기 때문에, 마지막 은행의 오른쪽 이웃이 첫 번째 은행으로 이어지는 원형 배열 구조를 고려해야 했다. 이를 위해 배열을 두 배 크기로 만들어 첫 번째 은행의 왼쪽 이웃이 마지막 은행과 연결되는 효과를 시뮬레이션했다.

2. 자본 합계 및 초기화: 각 은행의 자본을 입력받고, 음수인 경우 이를 양수로 전환하는 최소한의 마법 이동 횟수를 계산하는 것이 목적이므로, 전체 자본 합계를 구하는 것이 필요했다.

3. 최소 이동 횟수 계산: 각 은행의 부분 합을 구하면서, 특정 구간의 합이 음수인 경우 해당 값을 양수로 만들기 위한 이동 횟수를 누적해 최소 이동 횟수를 계산했다.

코드

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        long[] capital = new long[2 * N];
        long S = 0; // 전체 자본 합계를 저장

        // 자본 입력과 초기화
        for (int i = 0; i < N; i++) {
            capital[i] = sc.nextLong();
            capital[i + N] = capital[i]; // 순환을 위한 두 배 배열
            S += capital[i];
        }
        sc.close();

        // 누적 합 계산
        for (int i = 1; i < 2 * N; i++) {
            capital[i] += capital[i - 1];
        }

        long result = 0;
        // 최소 마법 이동 횟수 계산
        for (int i = 1; i < N; i++) {
            for (int j = 0; j < N; j++) {
                long subSum = capital[j + i] - capital[j];
                if (subSum < 0) {
                    result += Math.ceil((double) -subSum / S);
                }
            }
        }

        System.out.println(result);
    }
}

코드 설명

1. 자본 초기화 및 배열 확장

int N = sc.nextInt();
long[] capital = new long[2 * N];
long S = 0; // 전체 자본 합계를 저장

for (int i = 0; i < N; i++) {
    capital[i] = sc.nextLong();
    capital[i + N] = capital[i]; // 순환을 위한 두 배 배열
    S += capital[i];
}

• N: 은행의 개수를 입력받는다.
• capital: 순환 배열을 위한 배열로, 두 배 크기로 선언해 각 은행의 자본을 저장하고, 원형 구조를 표현한다.
• S: 전체 자본 합계를 구해 자본 부족을 해결하기 위한 기준값으로 사용된다.

2. 누적 합 계산

for (int i = 1; i < 2 * N; i++) {
    capital[i] += capital[i - 1];
}

• 누적 합을 계산해 capital 배열에 저장한다. 이를 통해 특정 구간의 자본 합을 효율적으로 계산할 수 있게 된다. 예를 들어, 구간 [j, j + i]의 자본 합은 capital[j + i] - capital[j]로 구할 수 있다.

3. 최소 마법 이동 횟수 계산

long result = 0;
for (int i = 1; i < N; i++) {
    for (int j = 0; j < N; j++) {
        long subSum = capital[j + i] - capital[j];
        if (subSum < 0) {
            result += Math.ceil((double) -subSum / S);
        }
    }
}

• subSum은 각 구간의 자본 합을 나타낸다. 만약 subSum이 음수인 경우, S를 기준으로 부족한 자본을 채우기 위해 마법 이동이 필요하다.
• result에 필요한 이동 횟수를 누적하며, Math.ceil을 사용해 부족한 자본을 정수 단위로 보충하는 횟수를 계산한다.

So...

순환형 배열을 구현하여 원형 연결된 자본 문제를 해결하는 기본적인 방법을 사용했지만 각 구간에 대해 중첩 루프를 사용하고 있어 시간 복잡도가 높아 최적화가 필요하다. 예를 들어, 각 구간의 음수 부분 합을 더 효율적으로 계산하거나 세그먼트 트리를 사용해 마법 이동 횟수를 더욱 빠르게 계산하는 방법을 고려할 수 있다.