11월 21일 - 성대나라의 물탱크[BOJ/18227]

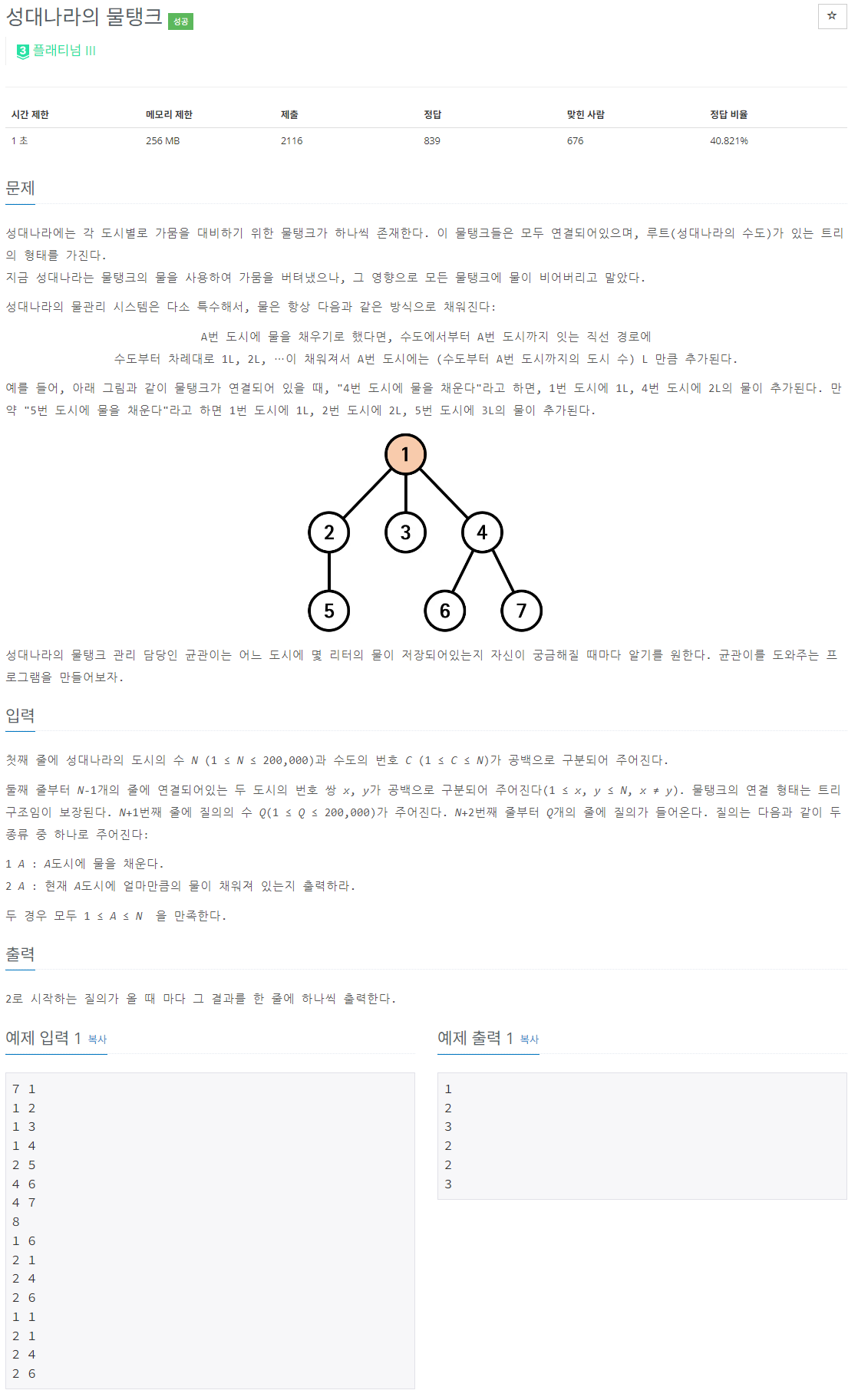
트리 구조에서 특정 노드와 그 경로에 대해 효율적으로 값을 갱신하고 쿼리를 처리하는 문제였다. 트리의 구조와 구간 연산을 결합하기 위해 오일러 경로 트릭(Euler Tour Trick)과 세그먼트 트리를 사용했다. 이를 통해 물 채우기 및 누적 물량 계산을 효율적으로 처리했다.

코드

import java.io.*;
import java.util.*;

public class Main {
    static int N, C, nodeNum = 0;
    static List<Integer>[] treeGraph;
    static int[][] indexTree;
    static long[] segmentTree, depth;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(System.out);
        StringTokenizer st;

        // 입력 처리
        st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        C = Integer.parseInt(st.nextToken());

        // 초기화
        treeGraph = new ArrayList[N + 1];
        indexTree = new int[N + 1][2];
        segmentTree = new long[4 * N];
        depth = new long[N + 1];

        for (int i = 1; i <= N; i++) treeGraph[i] = new ArrayList<>();

        // 트리 입력
        for (int i = 0; i < N - 1; i++) {
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            treeGraph[u].add(v);
            treeGraph[v].add(u);
        }

        // 깊이와 오일러 경로 설정
        depth[C] = 1;
        buildTree(C);

        // 쿼리 처리
        int Q = Integer.parseInt(br.readLine());
        for (int i = 0; i < Q; i++) {
            st = new StringTokenizer(br.readLine());
            int type = Integer.parseInt(st.nextToken());
            int city = Integer.parseInt(st.nextToken());

            if (type == 1) {
                update(1, 1, N, indexTree[city][0]);
            } else {
                long result = query(1, 1, N, indexTree[city][0], indexTree[city][1]) * depth[city];
                pw.println(result);
            }
        }

        pw.flush();
        pw.close();
    }

    // 트리 빌드 (DFS를 이용한 오일러 경로 트릭)
    static void buildTree(int current) {
        indexTree[current][0] = ++nodeNum;
        for (int neighbor : treeGraph[current]) {
            if (depth[neighbor] == 0) {
                depth[neighbor] = depth[current] + 1;
                buildTree(neighbor);
            }
        }
        indexTree[current][1] = nodeNum;
    }

    // 세그먼트 트리 업데이트
    static void update(int node, int start, int end, int pos) {
        if (pos < start || pos > end) return;
        segmentTree[node]++;
        if (start == end) return;
        int mid = (start + end) / 2;
        update(node * 2, start, mid, pos);
        update(node * 2 + 1, mid + 1, end, pos);
    }

    // 세그먼트 트리 쿼리
    static long query(int node, int start, int end, int l, int r) {
        if (r < start || l > end) return 0;
        if (l <= start && end <= r) return segmentTree[node];
        int mid = (start + end) / 2;
        return query(node * 2, start, mid, l, r) + query(node * 2 + 1, mid + 1, end, l, r);
    }
}

코드 설명

1. 트리 구조와 오일러 경로 구성

static void buildTree(int current) {
    indexTree[current][0] = ++nodeNum;
    for (int neighbor : treeGraph[current]) {
        if (depth[neighbor] == 0) {
            depth[neighbor] = depth[current] + 1;
            buildTree(neighbor);
        }
    }
    indexTree[current][1] = nodeNum;
}

• 트리의 DFS 순회를 통해 각 노드의 오일러 경로 범위(start, end)를 기록한다.
• depth 배열에 현재 노드의 깊이를 기록해 물량 계산 시 활용한다.

2. 세그먼트 트리 갱신 (update)

static void update(int node, int start, int end, int pos) {
    if (pos < start || pos > end) return;
    segmentTree[node]++;
    if (start == end) return;
    int mid = (start + end) / 2;
    update(node * 2, start, mid, pos);
    update(node * 2 + 1, mid + 1, end, pos);
}

• 특정 노드에 물을 채우는 경우, 해당 노드의 오일러 시작 인덱스에 해당하는 세그먼트 트리의 값을 증가시킨다.
• 부모 노드에서 자식 노드로 갱신이 이루어진다.

3. 세그먼트 트리 쿼리 (query)

static long query(int node, int start, int end, int l, int r) {
    if (r < start || l > end) return 0;
    if (l <= start && end <= r) return segmentTree[node];
    int mid = (start + end) / 2;
    return query(node * 2, start, mid, l, r) + query(node * 2 + 1, mid + 1, end, l, r);
}

• 특정 노드의 오일러 범위를 기반으로 구간 합을 계산한다.
• 구간 합 결과에 depth[city]를 곱해 해당 도시의 누적 물량을 계산한다.

4. 쿼리 처리

if (type == 1) {
    update(1, 1, N, indexTree[city][0]);
} else {
    long result = query(1, 1, N, indexTree[city][0], indexTree[city][1]) * depth[city];
    pw.println(result);
}

• type == 1: 특정 노드에 물을 채운다. 해당 노드의 오일러 시작 위치를 세그먼트 트리에 갱신한다.
• type == 2: 특정 노드의 누적 물량을 계산해 출력한다.

So...

트리 구조에서의 효율적인 구간 연산을 해결하기 위해 오일러 경로 트릭과 세그먼트 트리를 결합한 좋은 사례였다. 물 채우기와 누적 물량 계산이 모두 트리의 경로와 연관되기 때문에, 트리를 일렬로 펼치는 오일러 경로 방식이 적합했다. 이 접근법 덕분에 각 쿼리를 O(log N)에 처리할 수 있었으며, Lazy Propagation 없이도 효율적인 결과를 얻었다. 고민했던 점은 트리의 각 노드에서 구간 연산을 효율적으로 처리하는 방식이었으며, 오일러 경로와 세그먼트 트리의 결합이 매우 효과적이었다.