11월22일 - 다각형 게임[BOJ/13034]

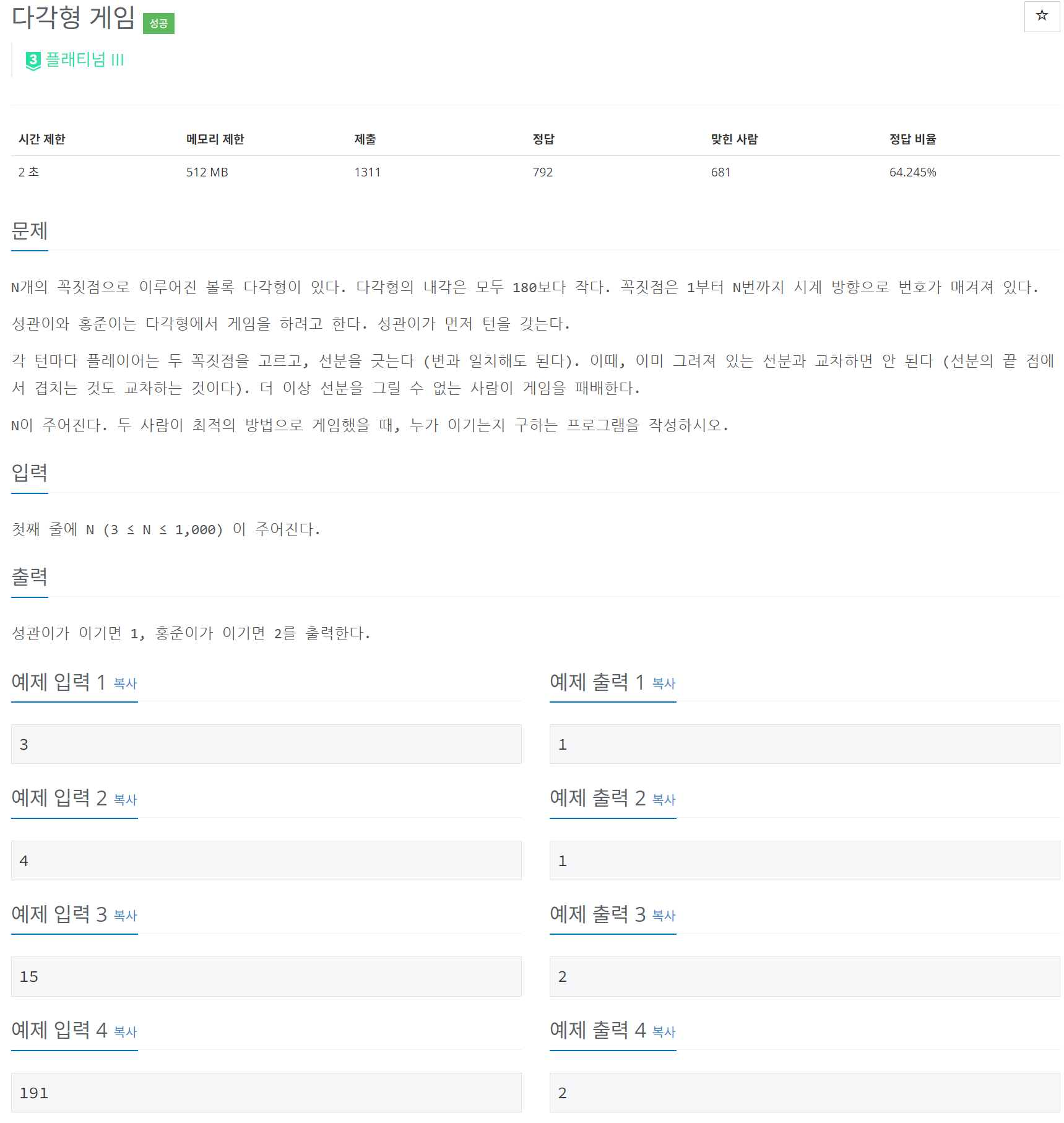
N-각형에서의 선 긋기 게임으로, 최적의 방법으로 플레이했을 때 어느 플레이어가 승리할지를 구하는 문제다. 게임 이론의 그룬디 수(Grundy Number)를 활용하여 최적의 해법을 도출했다. 그룬디 수는 컴비네토리얼 게임 이론에서 필수적인 개념으로, 각 상태에서 승패를 결정짓는 핵심 도구다.

코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[] DP = new int[n + 1]; // 다각형 크기별 Grundy 수를 저장하는 DP 배열

        for (int i = 2; i <= n; i++) {
            Set<Integer> grundySet = new HashSet<>();
            // 두 점을 잇는 가능한 모든 경우의 Grundy 수를 계산
            for (int j = 1; j < i; j++) {
                grundySet.add(DP[j - 1] ^ DP[i - 1 - j]);
            }

            // Grundy 수 계산: 가장 작은 비사용 값(Mex, Minimum Excludant)
            int grundy = 0;
            while (grundySet.contains(grundy)) {
                grundy++;
            }
            DP[i] = grundy;
        }

        // Grundy 수가 0이 아니면 첫 번째 플레이어 승리
        System.out.println(DP[n] != 0 ? 1 : 2);
    }
}

코드 설명

1. Grundy 수와 DP 배열 초기화

int[] DP = new int[n + 1];

• DP[i]는 i개의 꼭짓점을 가진 다각형의 Grundy 수를 저장한다.
• Grundy 수는 현재 상태가 승리 상태인지 패배 상태인지를 결정한다.
• Grundy 수가 0이면 패배 상태.
• Grundy 수가 0이 아니면 승리 상태.

2. Grundy 수 계산

for (int i = 2; i <= n; i++) {
    Set<Integer> grundySet = new HashSet<>();
    for (int j = 1; j < i; j++) {
        grundySet.add(DP[j - 1] ^ DP[i - 1 - j]);
    }

    int grundy = 0;
    while (grundySet.contains(grundy)) {
        grundy++;
    }
    DP[i] = grundy;
}

• 가능한 모든 상태를 탐색:
  • 두 점을 선택해 다각형을 나누고 각 부분에 대해 Grundy 수를 계산한다.
  • DP[j - 1] ^ DP[i - 1 - j]는 두 구간의 Grundy 수의 XOR 연산 결과다.
• Mex(Minimum Excludant) 계산:
  • Mex는 grundySet에 포함되지 않은 가장 작은 자연수다.
  • Grundy 수를 계산하기 위해 Mex를 사용한다.

3. 최종 출력

System.out.println(DP[n] != 0 ? 1 : 2);

• Grundy 수가 0이 아니면 첫 번째 플레이어가 승리하고, 0이면 두 번째 플레이어가 승리한다.

So...

이 문제는 게임 이론에서의 Grundy 수와 Mex 계산을 활용한 좋은 예제였다. Grundy 수를 통해 최적의 상태를 효율적으로 계산할 수 있었으며, 이를 DP 배열로 메모이제이션하여 성능을 최적화했다. 고민했던 점은 가능한 상태를 어떻게 효율적으로 탐색할지였으며, XOR 연산과 Mex 계산의 조합으로 이를 해결했다. 최종적으로 Grundy 수가 0인지 아닌지로 승패를 간단히 결정할 수 있었다.