11월28일 - 수열과 쿼리20[BOJ/16903]

문제 설명

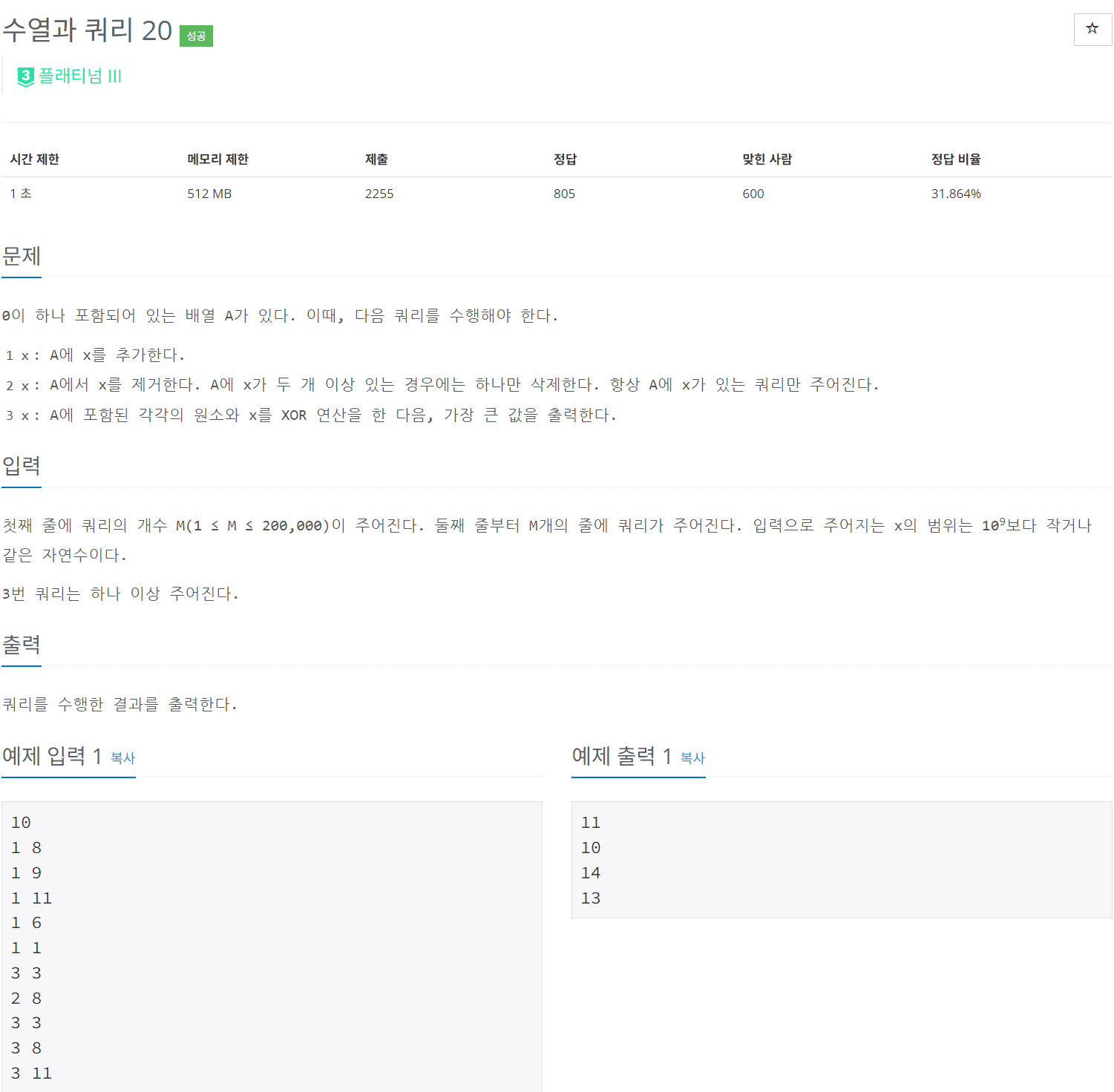
이 문제는 XOR 연산을 활용하여 효율적으로 결과를 계산하는 방법을 묻는다. 주어진 배열에서 다음과 같은 세 가지 쿼리를 수행해야 한다:

1. x: 배열 A에 정수 x를 추가한다.
2. x: 배열 A에서 정수 x를 제거한다. 단, 배열에 x가 반드시 존재하며 중복된 경우 하나만 제거한다.
3. x: 배열 A의 모든 원소에 대해 정수 x와 XOR 연산을 수행한 결과 중 가장 큰 값을 출력한다.

이 문제에서 주요 도전은 효율적으로 배열에 추가/삭제/최대 XOR 값을 찾는 것이다. 배열의 크기와 쿼리 수가 매우 크기 때문에, 이를 빠르게 처리하려면 트라이(Trie) 자료구조를 활용해야 한다.

코드

import java.io.*;
import java.util.*;

public class Main {

    static class Trie {
        int count;
        Trie[] node;

        public Trie() {
            count = 0;
            node = new Trie[2]; // 0과 1을 저장할 두 가지 노드
        }

        public void insert(BitSet bit, int idx) {
            count++;
            if (idx == -1) return;

            int bitValue = bit.get(idx) ? 1 : 0;
            if (node[bitValue] == null) {
                node[bitValue] = new Trie();
            }
            node[bitValue].insert(bit, idx - 1);
        }

        public void erase(BitSet bit, int idx) {
            count--;
            if (idx == -1) return;

            int bitValue = bit.get(idx) ? 1 : 0;
            node[bitValue].erase(bit, idx - 1);

            if (node[bitValue].count == 0) {
                node[bitValue] = null; // 자식 노드를 제거
            }
        }

        public int find(BitSet bit, BitSet result, int idx) {
            if (idx == -1) {
                return toInt(result);
            }

            int bitValue = bit.get(idx) ? 1 : 0;
            if (node[1 - bitValue] != null) { // 최대 XOR을 위해 반대 비트를 선택
                result.set(idx);
                return node[1 - bitValue].find(bit, result, idx - 1);
            } else {
                result.clear(idx);
                return node[bitValue].find(bit, result, idx - 1);
            }
        }

        private int toInt(BitSet bitSet) {
            int value = 0;
            for (int i = 0; i < 32; i++) {
                if (bitSet.get(i)) {
                    value |= (1 << i);
                }
            }
            return value;
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int m = Integer.parseInt(br.readLine());
        Trie root = new Trie();
        BitSet zero = new BitSet(32);
        root.insert(zero, 31); // 초기 값 0 추가

        while (m-- > 0) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int q = Integer.parseInt(st.nextToken());
            int x = Integer.parseInt(st.nextToken());

            BitSet bitSet = toBitSet(x);
            BitSet result = new BitSet(32);

            switch (q) {
                case 1:
                    root.insert(bitSet, 31);
                    break;
                case 2:
                    root.erase(bitSet, 31);
                    break;
                case 3:
                    int maxXOR = root.find(bitSet, result, 31);
                    bw.write(maxXOR + "\n");
                    break;
            }
        }

        bw.flush();
        bw.close();
    }

    private static BitSet toBitSet(int x) {
        BitSet bitSet = new BitSet(32);
        for (int i = 0; i < 32; i++) {
            if ((x & (1 << i)) != 0) {
                bitSet.set(i);
            }
        }
        return bitSet;
    }
}

코드 풀이 과정

1. 트라이(Trie) 자료구조 설계

• 각 노드는 0 또는 1의 두 가지 비트를 저장할 수 있다.
• 각 노드는 count를 유지하여 해당 노드를 공유하는 경로의 개수를 기록한다.
• 주요 메서드:
  • insert: 비트를 따라 노드를 추가한다.
  • erase: 비트를 따라 노드를 제거하고, 경로가 더 이상 사용되지 않으면 노드를 삭제한다.
  • find: XOR 연산에서 최대값을 만들기 위해 반대 비트를 우선 선택하며 탐색한다.

2. 쿼리 처리

쿼리 1: 추가

root.insert(bitSet, 31);

• 주어진 정수를 비트 형태로 변환 후, 트라이에 삽입한다.

쿼리 2: 삭제

root.erase(bitSet, 31);

• 주어진 정수를 비트 형태로 변환 후, 트라이에서 삭제한다.

쿼리 3: XOR 최대값 계산

int maxXOR = root.find(bitSet, result, 31);
bw.write(maxXOR + "\n");

• 주어진 정수의 XOR 최대값을 계산한다. 최대 XOR 값을 만들기 위해 현재 비트의 반대값을 우선 탐색한다.

3. 비트 변환

private static BitSet toBitSet(int x) {
    BitSet bitSet = new BitSet(32);
    for (int i = 0; i < 32; i++) {
        if ((x & (1 << i)) != 0) {
            bitSet.set(i);
        }
    }
    return bitSet;
}

• 정수를 비트셋(BitSet)으로 변환하여 트라이에 삽입하거나 탐색할 수 있게 한다.

So...

이 문제는 트라이 자료구조를 활용하여 XOR 연산의 최대값을 빠르게 계산하는 방법을 다룬다. 비트 단위로 탐색하며 시간 복잡도를 줄였으며, 효율적인 추가 및 삭제를 위해 노드의 count를 관리했다. 특히 XOR 최대값을 계산할 때 반대 비트를 우선 선택하는 전략이 핵심이다. 초기에는 트라이 자료구조와 비트셋의 사용이 복잡해 보였으나, 설계와 구현을 통해 문제를 효과적으로 해결할 수 있었다.