12월2일 - 점분리[BOJ/3878]

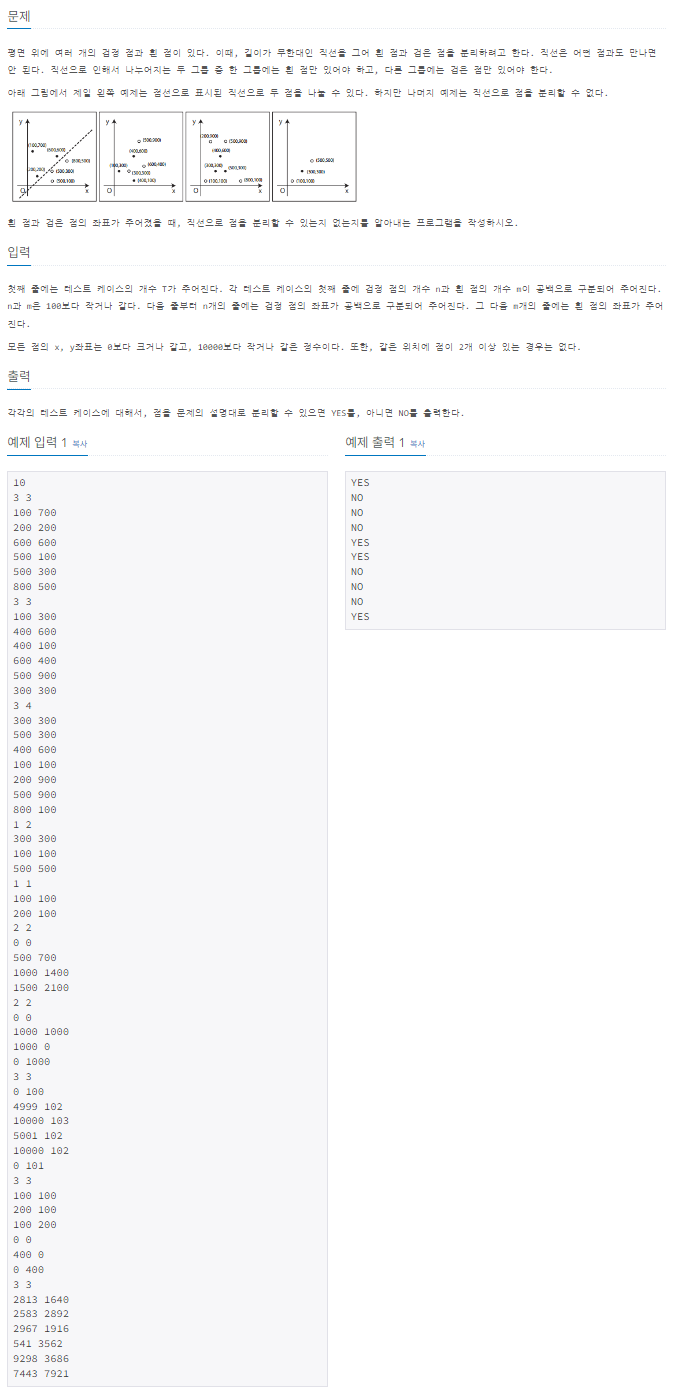
평면 위에 검정 점과 흰 점이 각각 여러 개 주어졌을 때, 한 개의 직선으로 두 점 집합을 완벽히 분리할 수 있는지 판별하는 문제이다.
직선은 어떤 점과도 만나지 않아야 하며, 분리된 영역 중 하나에는 흰 점만, 다른 하나에는 검정 점만 있어야 한다.
이 문제는 기하학적 알고리즘을 활용하여 해결할 수 있다.

코드

#include <iostream>
#include <vector>
#include <algorithm>

typedef long long ll;

// 점을 나타내는 구조체
struct Point {
    ll x, y, deltaX, deltaY;
    Point(ll x = 0, ll y = 0) : x(x), y(y), deltaX(1), deltaY(0) {}
    // 정렬 기준 정의: 기준점과의 방향 및 y, x 좌표 기준
    bool operator<(Point& other) {
        if (deltaX * other.deltaY ^ other.deltaX * deltaY) 
            return deltaX * other.deltaY > other.deltaX * deltaY;
        return y < other.y ? true : (y == other.y && x < other.x);
    }
};

// 세 점의 방향성을 계산하는 CCW 함수
ll inline computeCCW(const Point& p1, const Point& p2, const Point& p3) {
    ll result = p1.x * p2.y + p2.x * p3.y + p3.x * p1.y
                - p3.x * p2.y - p2.x * p1.y - p1.x * p3.y;
    return result > 0 ? 1 : result < 0 ? -1 : 0;
}

// 두 선분이 분리되었는지 확인
bool inline areDisjoint(ll a, ll b, ll c, ll d) {
    return std::max(a, b) < std::min(c, d) || std::min(a, b) > std::max(c, d);
}

int numBlackPoints, numWhitePoints;
std::vector<Point> blackPoints, whitePoints, blackHull, whiteHull;

// 볼록 껍질 계산 (Monotone Chain Algorithm)
void computeConvexHull(std::vector<Point>& points, std::vector<Point>& hull) {
    std::sort(points.begin(), points.end());
    for (int i = 1; i < points.size(); ++i) {
        points[i].deltaX = points[i].x - points[0].x;
        points[i].deltaY = points[i].y - points[0].y;
    }
    std::sort(points.begin() + 1, points.end());

    for (int i = 0; i < points.size(); ++i) {
        while (hull.size() >= 2 && computeCCW(hull[hull.size() - 2], hull.back(), points[i]) <= 0) {
            hull.pop_back();
        }
        hull.push_back(points[i]);
    }
}

// 점이 다각형 내부에 있는지 확인
bool isPointInside(const Point& point, const std::vector<Point>& hull) {
    ll initialDirection = computeCCW(hull[0], hull[1], point);
    for (int i = 1; i < hull.size(); ++i) {
        if (initialDirection * computeCCW(hull[i], hull[(i + 1) % hull.size()], point) <= 0) {
            return false;
        }
    }
    return true;
}

// 하나의 다각형이 다른 다각형 내부에 있는지 확인
bool isPolygonInside(const std::vector<Point>& polygonA, const std::vector<Point>& polygonB) {
    if (polygonB.size() > 2) {
        for (const Point& point : polygonA) {
            if (isPointInside(point, polygonB)) return true;
        }
    }
    return false;
}

// 두 선분이 교차하는지 확인
bool doSegmentsIntersect(const Point& a, const Point& b, const Point& c, const Point& d) {
    int directionAB = computeCCW(a, b, c) * computeCCW(a, b, d);
    int directionCD = computeCCW(c, d, a) * computeCCW(c, d, b);
    if (directionAB == 0 && directionCD == 0) {
        return !areDisjoint(a.x, b.x, c.x, d.x) && !areDisjoint(a.y, b.y, c.y, d.y);
    }
    return directionAB <= 0 && directionCD <= 0;
}

// 두 다각형의 선분이 교차하는지 확인
bool doPolygonsOverlap(const std::vector<Point>& polygonA, const std::vector<Point>& polygonB) {
    int n = polygonA.size(), m = polygonB.size();
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            if (doSegmentsIntersect(polygonA[i], polygonA[(i + 1) % n], polygonB[j], polygonB[(j + 1) % m])) {
                return true;
            }
        }
    }
    return false;
}

// 문제 풀이 함수
void solve() {
    blackPoints.clear();
    whitePoints.clear();
    blackHull.clear();
    whiteHull.clear();

    std::cin >> numBlackPoints >> numWhitePoints;
    for (ll x, y, i = 0; i < numBlackPoints; ++i) {
        std::cin >> x >> y;
        blackPoints.push_back(Point(x, y));
    }
    for (ll x, y, i = 0; i < numWhitePoints; ++i) {
        std::cin >> x >> y;
        whitePoints.push_back(Point(x, y));
    }
    computeConvexHull(blackPoints, blackHull);
    computeConvexHull(whitePoints, whiteHull);

    if (isPolygonInside(blackHull, whiteHull) || 
        isPolygonInside(whiteHull, blackHull) || 
        doPolygonsOverlap(blackHull, whiteHull)) {
        std::cout << "NO\n";
    } else {
        std::cout << "YES\n";
    }
}

int main() {
    int testCases;
    std::cin >> testCases;
    while (testCases--) solve();
}

풀이 과정

CCW (Counter Clockwise)

• 세 점의 방향성을 판단하여, 선분이 시계 방향인지, 반시계 방향인지, 혹은 직선에 있는지를 계산한다.

Convex Hull 생성

• 주어진 흰 점과 검정 점 각각에 대해 Monotone Chain 알고리즘으로 볼록 껍질을 생성한다.
• 볼록 껍질은 다각형의 외곽을 나타내며, 점 집합의 경계를 나타낸다.

점과 다각형의 관계 확인

• 흰 점 중 하나가 검정 점 볼록 껍질 내부에 있는지, 또는 검정 점 중 하나가 흰 점 볼록 껍질 내부에 있는지를 확인한다.

다각형의 선분 교차 확인

• 두 다각형의 선분이 교차하는지 확인한다. 교차 시 두 점 집합을 직선으로 분리할 수 없다.

결과 도출

• 위 조건 중 하나라도 충족되면 분리가 불가능하며 "NO"를 출력, 아니면 "YES"를 출력한다.

So...

이 문제는 기하학적 알고리즘(볼록 껍질, CCW 등)을 이용한 고급 분리 문제로, 교차 검출 및 다각형 내부 확인 과정에서 효율적 자료 구조와 알고리즘의 중요성을 깨달았다. 고민했던 부분은 볼록 껍질 생성 및 교차 판단의 정확성이었고, 이를 통해 구현의 정확도와 효율성 모두를 만족시킬 수 있었다.