12월 10일 - 달리기 [BOJ/12963]

Yullgiii·2024년 12월 9일

개발자로의 취업을 준비하며 TIL

목록 보기

330/363

문제 설명

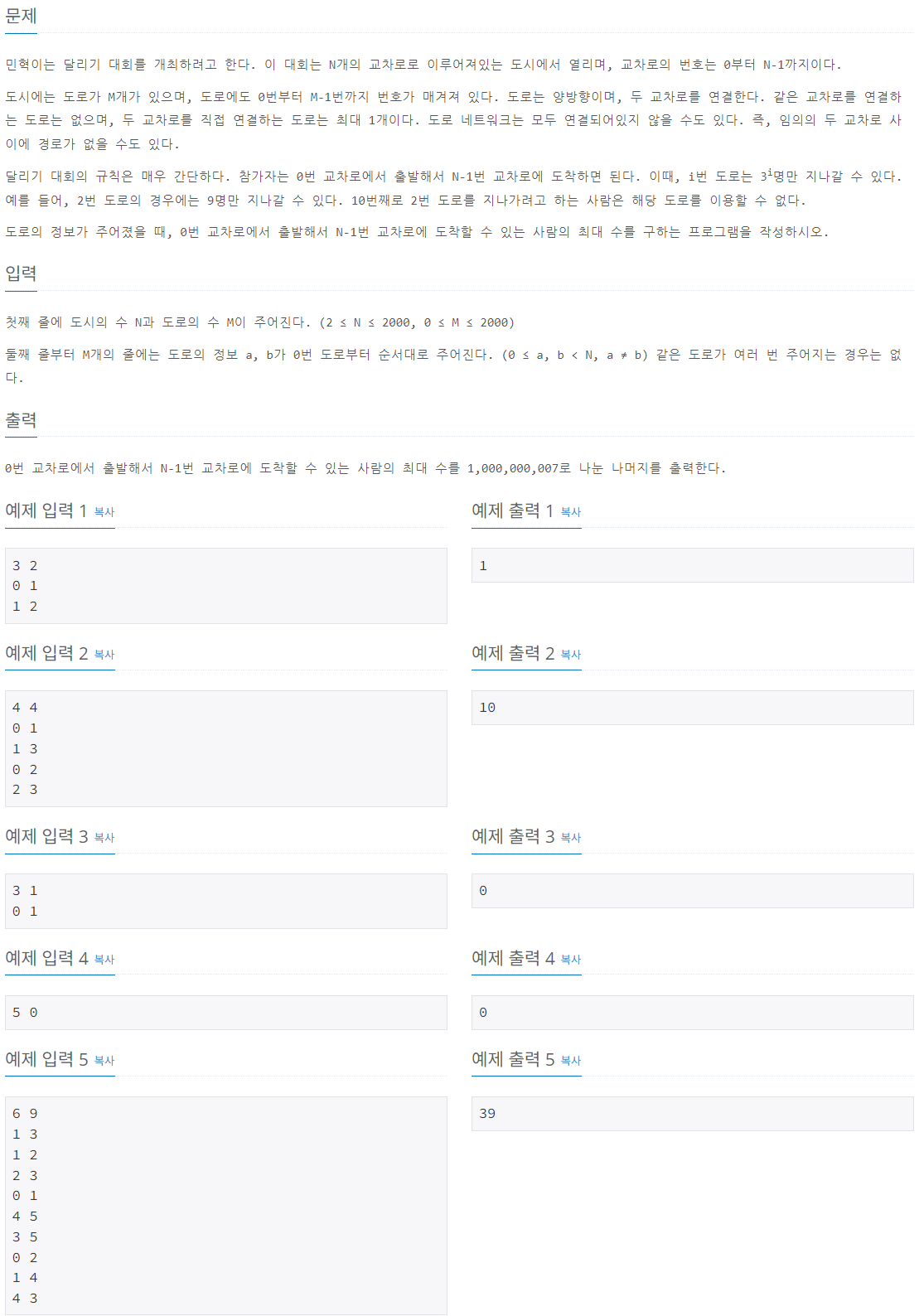
이 문제는 무방향 그래프에서 0번 교차로에서 (N-1)번 교차로까지 이동할 수 있는 최대 사람 수를 구하는 문제다.
각 도로는 번호가 부여되어 있으며, (i)번 도로는 (3^i)명만 통과 가능하다.
따라서 도로를 역순으로 추가하면서, 최대 이동 인원을 점진적으로 계산해야 한다.

문제의 핵심은 Union-Find 알고리즘을 사용해 연결성을 관리하면서, 도로가 추가될 때마다 연결 상태를 점검하고 결과를 갱신하는 것이다.

코드

import java.io.*;
import java.util.*;

public class Main {
    static final long MOD = 1_000_000_007;
    static int n, m;
    static int[] parent;
    static long[] powerOfThree;
    static long answer = 0;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        // 입력 처리
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());

        int[] a = new int[m];
        int[] b = new int[m];

        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            a[i] = Integer.parseInt(st.nextToken()) + 1;
            b[i] = Integer.parseInt(st.nextToken()) + 1;
        }

        // 3의 거듭제곱 계산
        powerOfThree = new long[m + 1];
        powerOfThree[0] = 1;
        for (int i = 1; i <= m; i++) {
            powerOfThree[i] = (powerOfThree[i - 1] * 3) % MOD;
        }

        // Union-Find 초기화
        parent = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            parent[i] = i;
        }

        // 역순으로 간선 처리
        for (int i = m - 1; i >= 0; i--) {
            union(a[i], b[i], i);
        }

        // 결과 출력
        System.out.println(answer);
    }

    // Find 함수: 경로 압축(Path Compression) 적용
    static int find(int x) {
        if (parent[x] == x) {
            return x;
        }
        return parent[x] = find(parent[x]);
    }

    // Union 함수: 간선 연결 및 결과 갱신
    static void union(int u, int v, int weightIndex) {
        int rootU = find(u);
        int rootV = find(v);

        // 이미 같은 집합이면 처리할 필요 없음
        if (rootU == rootV) {
            return;
        }

        // 작은 번호를 부모로 설정
        if (rootU > rootV) {
            int temp = rootU;
            rootU = rootV;
            rootV = temp;
        }

        // 1번과 N번이 연결되는 경우
        if (rootU == 1 && rootV == n) {
            answer = (answer + powerOfThree[weightIndex]) % MOD;
        } else if (rootU == 1) {
            parent[rootV] = rootU;
        } else {
            parent[rootU] = rootV;
        }
    }
}

코드 설명

주요 함수 및 과정

Union-Find 초기화

parent = new int[n + 1];
for (int i = 1; i <= n; i++) {
    parent[i] = i;
}

parent 배열은 각 정점의 대표(root) 정점을 저장한다.
초기 상태에서는 각 정점이 자신의 대표로 설정된다.

3의 거듭제곱 계산

powerOfThree = new long[m + 1];
powerOfThree[0] = 1;
for (int i = 1; i <= m; i++) {
    powerOfThree[i] = (powerOfThree[i - 1] * 3) % MOD;
}

각 도로의 최대 통행량 (3^i) 미리 계산한다. 이를 통해 계산 속도를 향상시킨다.

Find 함수

static int find(int x) {
    if (parent[x] == x) {
        return x;
    }
    return parent[x] = find(parent[x]);
}

Find는 경로 압축(Path Compression)을 사용하여, 트리의 깊이를 줄이고 연산을 최적화한다.

Union 함수

static void union(int u, int v, int weightIndex) {
    int rootU = find(u);
    int rootV = find(v);

    if (rootU == rootV) {
        return;
    }

    if (rootU > rootV) {
        int temp = rootU;
        rootU = rootV;
        rootV = temp;
    }

    if (rootU == 1 && rootV == n) {
        answer = (answer + powerOfThree[weightIndex]) % MOD;
    } else if (rootU == 1) {
        parent[rootV] = rootU;
    } else {
        parent[rootU] = rootV;
    }
}