12월 5일 - TV Show Game[BOJ/16367]

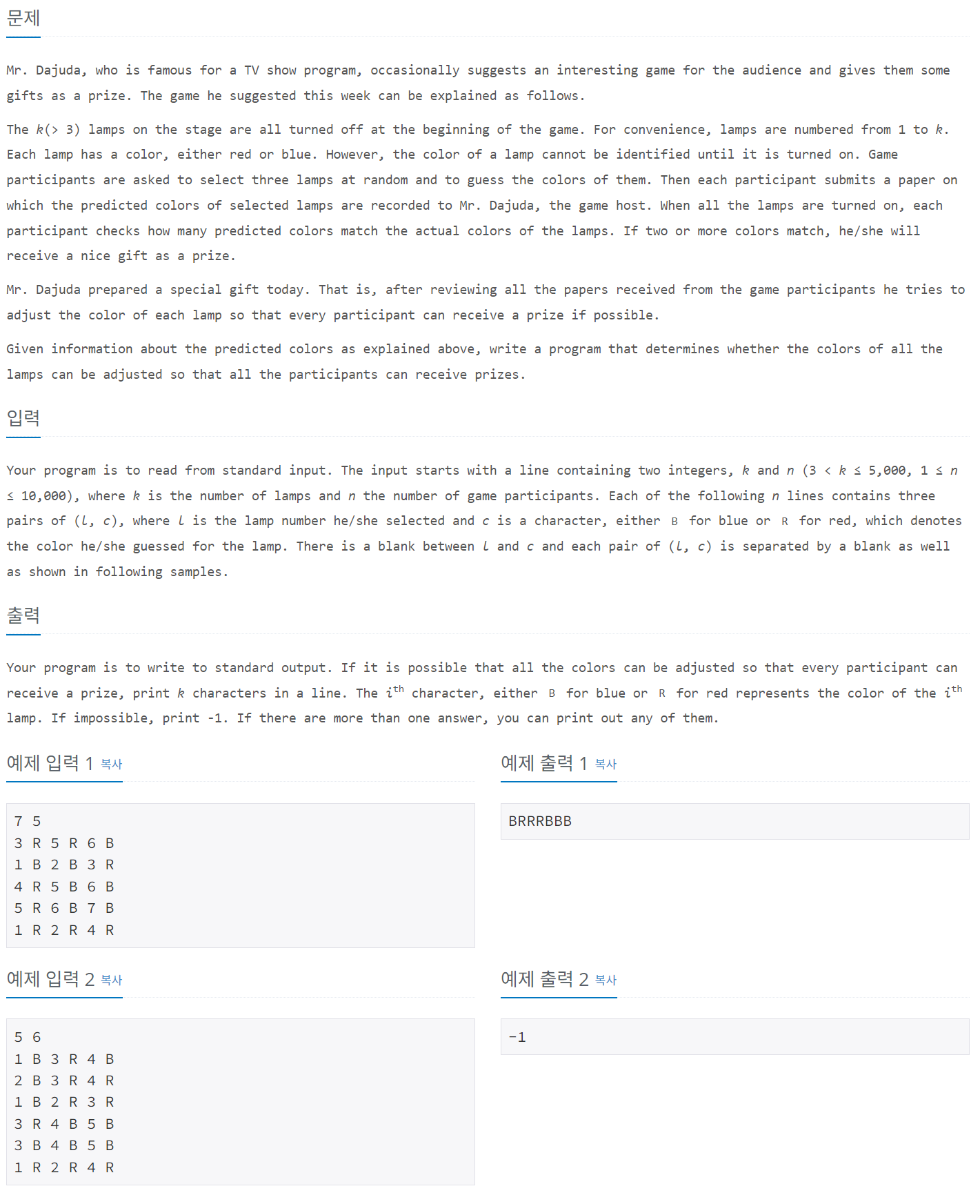
문제 설명

배열 A가 주어지고, 다음과 같은 Q개의 쿼리를 처리하는 문제이다:

• 쿼리 형태: l r
  배열의 l번째부터 r번째까지의 구간에서 서로 다른 수의 개수를 출력한다.

제약 조건

1. 배열의 크기 N: 최대 1,000,000
2. 쿼리의 개수 Q: 최대 1,000,000
3. 각 수의 크기: 최대 1,000,000,000 이하의 자연수

문제 요구사항

• 각 쿼리에 대해 구간 [l, r]에서 서로 다른 수의 개수를 효율적으로 계산해야 한다.

Code

import java.io.*;
import java.util.*;

public class Main {

    static int n, m;
    static List<List<Integer>> graph = new ArrayList<>();
    static Stack<Integer> stack = new Stack<>();
    static int[] low, dfn, sccId;
    static boolean[] visited;
    static int nodeNum = 0, sccCount = 0;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        n = Integer.parseInt(st.nextToken()); // 램프 개수
        m = Integer.parseInt(st.nextToken()); // 참가자 수

        int totalNodes = 2 * n;
        low = new int[totalNodes + 1];
        dfn = new int[totalNodes + 1];
        sccId = new int[totalNodes + 1];
        visited = new boolean[totalNodes + 1];

        Arrays.fill(dfn, -1);

        for (int i = 0; i <= totalNodes; i++) {
            graph.add(new ArrayList<>());
        }

        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            char c1 = st.nextToken().charAt(0);
            int x2 = Integer.parseInt(st.nextToken());
            char c2 = st.nextToken().charAt(0);
            int x3 = Integer.parseInt(st.nextToken());
            char c3 = st.nextToken().charAt(0);

            x1 = (c1 == 'R' ? x1 : notX(x1));
            x2 = (c2 == 'R' ? x2 : notX(x2));
            x3 = (c3 == 'R' ? x3 : notX(x3));

            // 2-SAT 조건 추가
            graph.get(notX(x1)).add(x2);
            graph.get(notX(x2)).add(x1);
            graph.get(notX(x2)).add(x3);
            graph.get(notX(x3)).add(x2);
            graph.get(notX(x3)).add(x1);
            graph.get(notX(x1)).add(x3);
        }

        // Tarjan 알고리즘 실행
        for (int i = 1; i <= totalNodes; i++) {
            if (dfn[i] == -1) {
                tarjan(i);
            }
        }

        // 유효한 해 검증
        for (int i = 1; i <= n; i++) {
            if (sccId[i] == sccId[notX(i)]) {
                System.out.println("-1");
                return;
            }
        }

        // 램프 색상 결정
        char[] result = new char[n + 1];
        for (int i = 1; i <= n; i++) {
            result[i] = (sccId[i] < sccId[notX(i)]) ? 'R' : 'B';
        }

        // 결과 출력
        for (int i = 1; i <= n; i++) {
            System.out.print(result[i]);
        }
    }

    // Negate a node
    private static int notX(int x) {
        return x > n ? x - n : x + n;
    }

    // Tarjan's algorithm for SCC
    private static void tarjan(int current) {
        low[current] = dfn[current] = ++nodeNum;
        stack.push(current);
        visited[current] = true;

        for (int next : graph.get(current)) {
            if (dfn[next] == -1) {
                tarjan(next);
                low[current] = Math.min(low[current], low[next]);
            } else if (visited[next]) {
                low[current] = Math.min(low[current], dfn[next]);
            }
        }

        if (low[current] == dfn[current]) {
            while (true) {
                int node = stack.pop();
                visited[node] = false;
                sccId[node] = sccCount;
                if (node == current) break;
            }
            sccCount++;
        }
    }
}

풀이 과정

1. 2-SAT 문제 정의

   • 참가자가 예상한 색상 조건은 2-SAT 문제로 변환할 수 있다.
   • x와 notX로 표현하여 각 조건을 논리식으로 변환:
     • 예를 들어, e1 = R, e2 = B인 경우:
       • notX(e1) → e2
       • notX(e2) → e1

2. 그래프 구성

   • x와 notX(x)를 노드로 그래프를 구성한다.
   • 강결합 요소(SCC)를 이용해 x와 notX(x)가 같은 SCC에 속하면 모순 발생으로 판단.

3. Tarjan's Algorithm

   • 강결합 요소(SCC)를 찾기 위해 Tarjan 알고리즘을 사용.
   • 각 노드의 방문 순서와 저위값(low)을 통해 SCC를 구성.

4. 색상 결정

   • 모든 x와 notX(x)가 서로 다른 SCC에 속한다면:
     • SCC 순서를 기준으로 x의 색상을 결정.
     • sccId[x] < sccId[notX(x)]이면 빨간색, 아니면 파란색.

So...

이 문제는 2-SAT 문제를 그래프와 SCC 탐색으로 해결한 사례다.
특히, 조건의 논리식 변환과 SCC를 이용한 모순 판별이 핵심이었다.
문제를 풀며 논리식 전환과 Tarjan 알고리즘의 활용을 다시 복습할 수 있었다.

효율적으로 (O(V + E))로 해결할 수 있어 대규모 입력도 처리 가능하다.