Wall Making Game 문제 풀이 (Grundy 수 기반 최적 게임 이론)

문제 설명

Wall Making Game은 두 명의 플레이어가 ( H \times W ) 크기의 보드에서 번갈아가며 움직이는 게임이다. 게임 규칙은 다음과 같다:
1. 플레이어는 비어있는 셀을 선택한다. (이미 마킹된 셀이나 벽은 선택 불가)
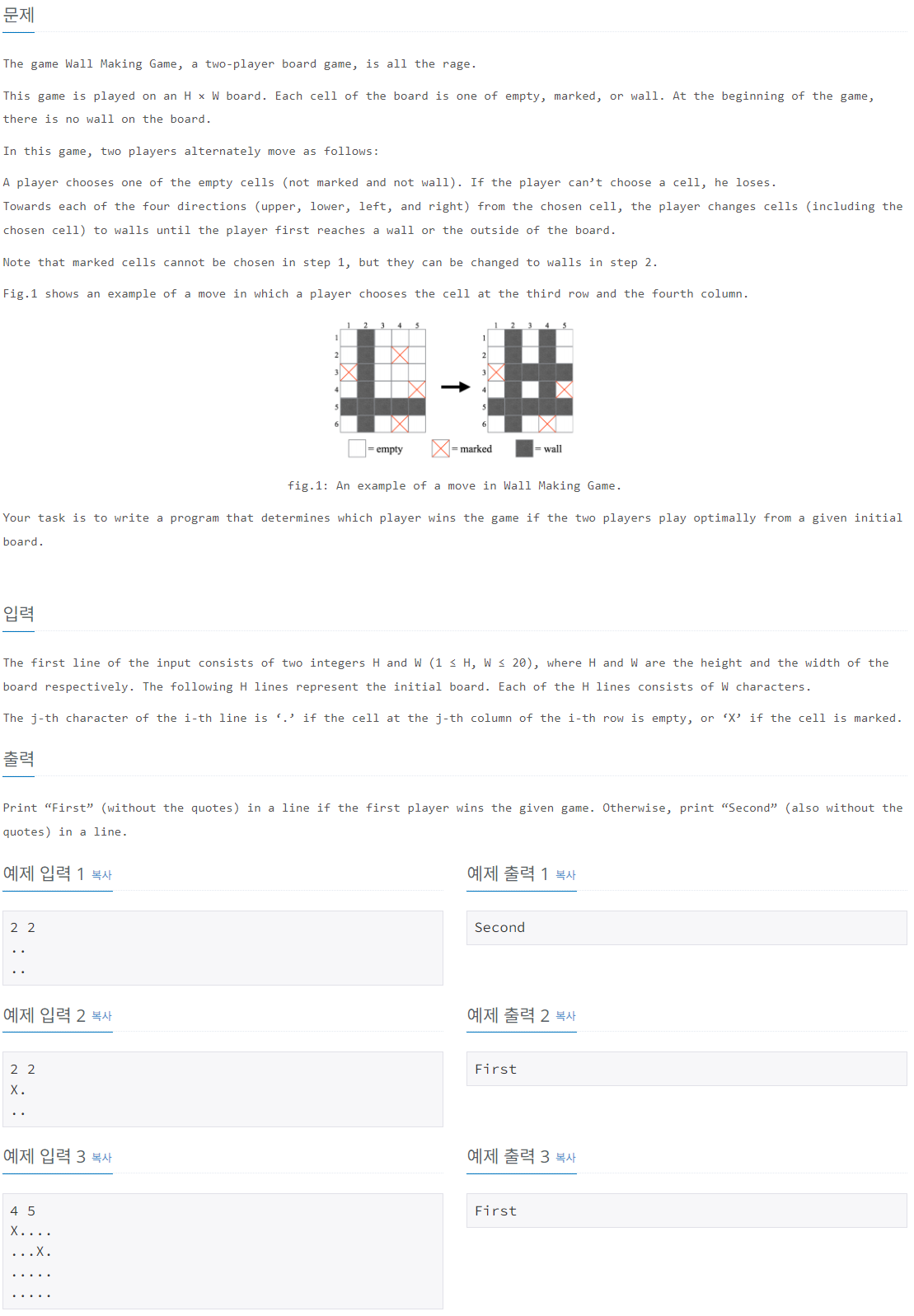
2. 선택된 셀을 중심으로 네 방향 (위, 아래, 왼쪽, 오른쪽) 으로 벽을 쌓아 올린다.

• 벽을 쌓는 과정은 첫 번째로 도달하는 벽이나 보드의 끝까지 확장된다.
• 마킹된 셀도 벽으로 바뀔 수 있다.

3. 만약 플레이어가 선택할 수 있는 셀이 없다면, 그 플레이어는 패배한다.

두 플레이어가 최적의 방법으로 게임을 진행할 때, 첫 번째 플레이어가 이길 수 있는지 판별하는 문제이다.

핵심 개념: Grundy 수와 최적 게임 이론

이 문제는 Nim 게임과 같은 형태를 갖기 때문에 Grundy 수를 이용해 해결할 수 있다.

1. Grundy 수의 정의:

   • Grundy 수는 현재 상태에서 최적의 움직임이 가능한 게임의 상태를 수치화한 값이다.
   • 상태 ( G )의 Grundy 수를 구할 때, 가능한 모든 다음 상태의 Grundy 수를 계산한 후, 그 값들의 Mex (Minimum Excludant) 를 Grundy 수로 한다.

2. 게임 이론의 원리:

   • Grundy 수가 0이면 패배 상태이다. (Second 승리)
   • Grundy 수가 0이 아니면 승리 상태이다. (First 승리)

코드

전체 코드

import java.util.*;

public class Main {
    static int H, W;
    static int[][] board;
    static int[][][][] D; // 메모이제이션 배열 (4차원 Grundy 값)

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        H = sc.nextInt(); // 보드의 높이
        W = sc.nextInt(); // 보드의 너비

        board = new int[H + 1][W + 1]; // 1-based 인덱싱
        D = new int[H + 2][H + 2][W + 2][W + 2]; // Grundy 메모이제이션

        for (int i = 1; i <= H; i++) {
            String row = sc.next();
            for (int j = 1; j <= W; j++) {
                board[i][j] = (row.charAt(j - 1) == 'X') ? 1 : 0; // 'X'는 마킹된 칸
            }
        }

        for (int[][][] d1 : D) {
            for (int[][] d2 : d1) {
                for (int[] d3 : d2) {
                    Arrays.fill(d3, -1); // Grundy 메모이제이션 초기화
                }
            }
        }

        if (Grundy(1, H, 1, W) != 0) {
            System.out.println("First");
        } else {
            System.out.println("Second");
        }
    }

    // Grundy 값 계산
    static int Grundy(int r1, int r2, int c1, int c2) {
        if (r1 < 1 || c1 < 1 || r2 > H || c2 > W || r1 > r2 || c1 > c2) return 0;

        if (D[r1][r2][c1][c2] != -1) return D[r1][r2][c1][c2];

        Set<Integer> grundySet = new HashSet<>();

        for (int i = r1; i <= r2; i++) {
            for (int j = c1; j <= c2; j++) {
                if (board[i][j] == 1) continue; // 이미 마킹된 칸은 건너뛴다.

                // 네 방향으로 나누어 Grundy 값을 XOR
                int g1 = Grundy(r1, i - 1, c1, j - 1);
                int g2 = Grundy(r1, i - 1, j + 1, c2);
                int g3 = Grundy(i + 1, r2, c1, j - 1);
                int g4 = Grundy(i + 1, r2, j + 1, c2);

                grundySet.add(g1 ^ g2 ^ g3 ^ g4);
            }
        }

        int mex = 0;
        while (grundySet.contains(mex)) mex++; // Grundy 수의 최솟값 (Mex)

        return D[r1][r2][c1][c2] = mex;
    }
}

코드 설명

1. 입력 및 초기화

• 보드의 높이 𝐻와 너비 𝑊를 입력받는다.
• 보드 정보는 2차원 배열 board에 저장한다.
• Grundy 수 계산을 위해 4차원 메모이제이션 배열 𝐷를 초기화한다.

2. Grundy 수 계산 (Grundy 함수)

• Grundy(r1, r2, c1, c2):
  • 현재 보드 영역에서 가능한 모든 선택지에 대해 Grundy 값을 계산한다.
  • 각 선택지에 대해 네 방향으로 영역을 나눈다:
    • 위쪽: Grundy(r1, i-1, c1, j-1)
    • 아래쪽: Grundy(i+1, r2, c1, j-1)
• 왼쪽 및 오른쪽도 같은 방식으로 처리한다.
• 가능한 모든 다음 상태의 Grundy 값에 대해 XOR 연산을 수행하고 Mex 값을 구한다.

3. 최종 게임 결과

• 𝐺𝑟𝑢𝑛𝑑𝑦(1,𝐻,1,𝑊) 값이 0이면 Second가 이긴다.
• 𝐺𝑟𝑢𝑛𝑑𝑦(1,𝐻,1,𝑊) 값이 0이 아니면 First가 이긴다.

So...

이 문제는 Grundy 수와 Mex 계산을 이용한 최적 게임 이론의 전형적인 예시이다.
처음에는 네 방향으로 영역을 나누는 부분이 어려웠지만, 작은 문제로 나누어 메모이제이션을 적용하니 최적의 성능을 보였다.
Grundy 값을 기반으로 게임의 승패를 판별하는 방법을 다시 복습하게 되었고, 최적화된 접근법의 중요성을 깨달았다.