트리 외심 찾기 문제 해결 (LCA 활용)

문제 설명

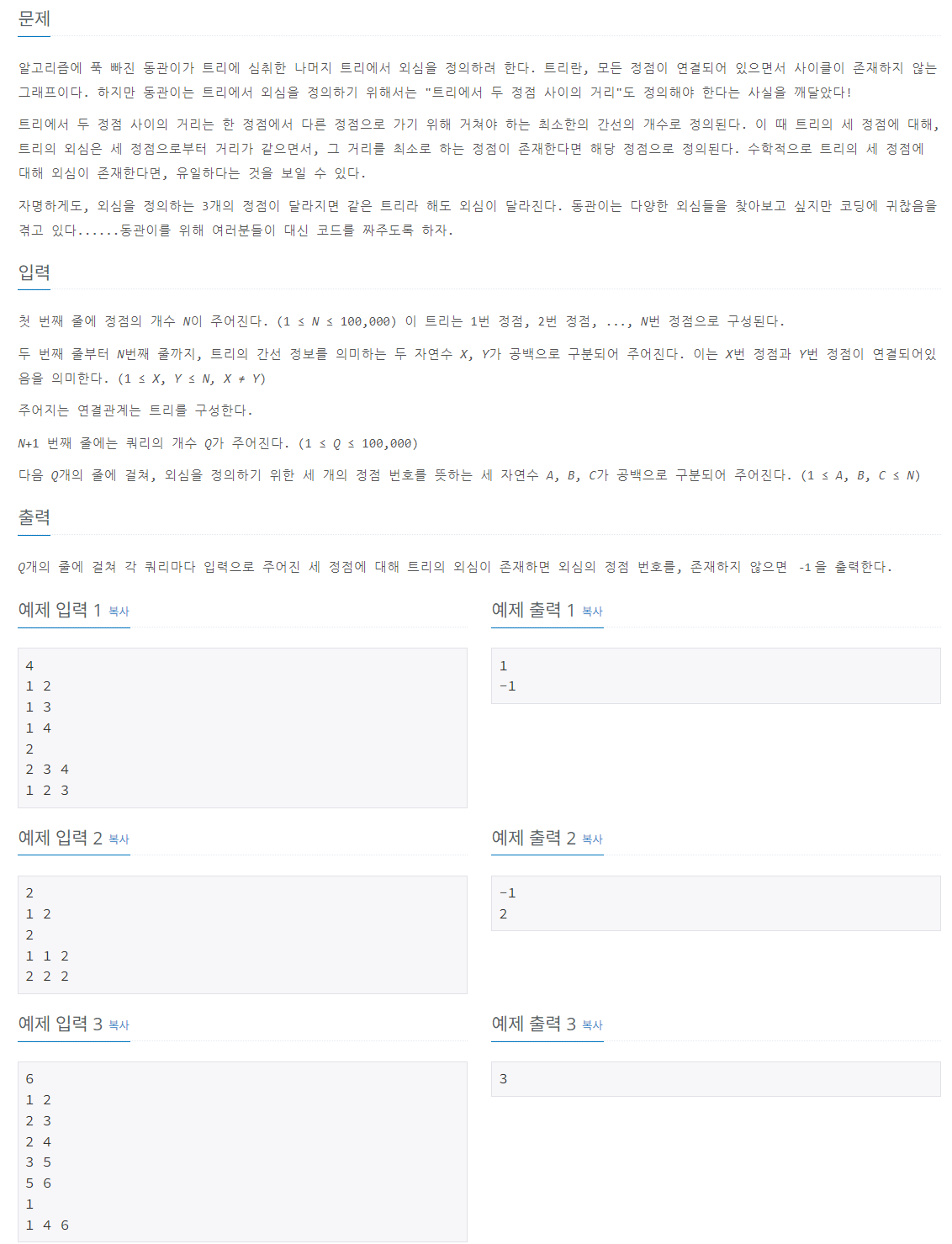
주어진 문제는 트리에서 세 개의 특정 정점으로부터의 거리가 같고 최소인 정점(외심)을 찾는 것이다. 주어진 입력으로 트리를 구성하고, 특정 세 정점 (A, B, C)에 대해:

• 외심이 존재하면 해당 정점 번호를 출력
• 존재하지 않으면 (-1) 출력

이 문제는 트리의 특성과 최소 공통 조상 (Lowest Common Ancestor, LCA) 알고리즘을 활용해 풀 수 있다.

핵심 아이디어

1. 트리에서 두 정점 사이의 거리:

   • 트리에서 두 정점 간의 거리는 LCA를 활용하여 계산 가능하다.
   • 두 정점 (u, v) 간 거리:
     [
     \text{dist}(u, v) = \text{depth}(u) + \text{depth}(v) - 2 \times \text{depth}(\text{LCA}(u, v))
     ]

2. 외심 후보 계산:

   • 세 정점 (A, B, C)의 외심 후보는 (A)와 (B), (A)와 (C), (B)와 (C) 간 중간 정점(midpoint)이다.
   • 두 정점 간 거리가 짝수여야 외심 후보가 될 수 있다.
   • 중간 정점에서 다른 정점까지의 거리가 동일한지 확인해야 한다.

3. LCA 전처리:

   • 트리의 깊이 및 부모 정보를 미리 계산하여 LCA를 효율적으로 구할 수 있도록 한다.
   • (O(N \log N)) 시간 복잡도로 전처리 후, 각 쿼리는 (O(\log N))에 해결 가능하다.

코드

#include <bits/stdc++.h>
using namespace std;
#define MAX 100001

// 배열 depth는 각 노드의 깊이를 저장
int nodeDepth[MAX], parent[MAX][20];
vector<int> adjacencyList[MAX];

// LCA 테이블 생성
void generateLcaTable(int currentNode, int parentNode, int depth){
    nodeDepth[currentNode] = depth;
    parent[currentNode][0] = parentNode;
    for (int i = 1; i < 20; i++) {
        parent[currentNode][i] = parent[parent[currentNode][i - 1]][i - 1];
    }

    // 트리를 순회하며 자식 노드 탐색
    for (auto nextNode : adjacencyList[currentNode]) {
        if (nextNode == parentNode) continue;
        generateLcaTable(nextNode, currentNode, depth + 1);
    }
}

// 두 노드의 LCA를 찾는 함수
int findLca(int node1, int node2){
    if (nodeDepth[node1] < nodeDepth[node2]) swap(node1, node2);

    // 깊이를 맞추기 위해 node1을 이동
    for (int i = 19; i >= 0; i--) {
        if (nodeDepth[node1] - nodeDepth[node2] >= (1 << i)) {
            node1 = parent[node1][i];
        }
    }
    if (node1 == node2) return node1;

    // 두 노드가 같은 부모를 가질 때까지 이동
    for (int i = 19; i >= 0; i--) {
        if (parent[node1][i] != parent[node2][i]) {
            node1 = parent[node1][i];
            node2 = parent[node2][i];
        }
    }

    return parent[node1][0];
}

// 두 노드 간의 거리 계산
int calculateDistance(int node1, int node2){
    int lowestCommonAncestor = findLca(node1, node2);
    return nodeDepth[node1] + nodeDepth[node2] - 2 * nodeDepth[lowestCommonAncestor];
}

// 특정 노드에서 특정 거리만큼 위로 이동
int moveUp(int node, int distance){
    for (int i = 0; i < 20; i++) {
        if (distance & (1 << i)) {
            node = parent[node][i];
        }
    }
    return node;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int totalNodes; cin >> totalNodes;
    for (int i = 0; i < totalNodes - 1; i++) {
        int node1, node2; cin >> node1 >> node2;
        adjacencyList[node1].push_back(node2);
        adjacencyList[node2].push_back(node1);
    }

    generateLcaTable(1, 0, 1);

    int queries; cin >> queries;
    while (queries--) {
        int nodeA, nodeB, nodeC; cin >> nodeA >> nodeB >> nodeC;

        int distance;
        // (nodeA, nodeB) 간의 외심 후보
        distance = calculateDistance(nodeA, nodeB);
        if (distance % 2 == 0){
            int midpoint = moveUp(nodeDepth[nodeA] > nodeDepth[nodeB] ? nodeA : nodeB, distance / 2);
            if (calculateDistance(midpoint, nodeC) == distance / 2){
                cout << midpoint << '\n';
                continue;
            }
        }

        // (nodeA, nodeC) 간의 외심 후보
        distance = calculateDistance(nodeA, nodeC);
        if (distance % 2 == 0){
            int midpoint = moveUp(nodeDepth[nodeA] > nodeDepth[nodeC] ? nodeA : nodeC, distance / 2);
            if (calculateDistance(midpoint, nodeB) == distance / 2){
                cout << midpoint << '\n';
                continue;
            }
        }

        // (nodeB, nodeC) 간의 외심 후보
        distance = calculateDistance(nodeB, nodeC);
        if (distance % 2 == 0){
            int midpoint = moveUp(nodeDepth[nodeB] > nodeDepth[nodeC] ? nodeB : nodeC, distance / 2);
            if (calculateDistance(midpoint, nodeA) == distance / 2){
                cout << midpoint << '\n';
                continue;
            }
        }

        cout << -1 << '\n';
    }
    return 0;
}

코드 설명

1. 입력 처리 및 LCA 전처리

• 트리를 입력받아 인접 리스트(adjacencyList)를 구성한다.
• generateLcaTable 함수는 DFS를 이용해 각 노드의 깊이 및 부모 정보를 계산한다.

2. 거리 및 외심 후보 계산

• calculateDistance 함수는 두 노드 간의 거리를 LCA를 통해 계산한다.
• moveUp 함수는 특정 노드에서 위로 이동해 중간 정점을 찾는다.
• 각 쿼리에 대해 𝐴,𝐵,𝐶의 외심 후보를 계산하고, 조건에 부합하면 출력한다.

3. 쿼리 처리

• 𝐴,𝐵,𝐶세 정점에 대해 각각 외심 후보를 계산한다.
• 외심이 존재하면 정점 번호를 출력하고, 없으면 −1을 출력한다.

So....

이 문제는 트리, LCA, 거리 계산과 같은 알고리즘적 개념을 활용하여 풀 수 있는 문제였다. LCA의 활용과 트리 구조 탐색이 중요한 핵심이었다. 최적화된 거리 계산과 조건 검증을 통해 쿼리를 효율적으로 처리할 수 있었다.