1월 13일 - Oil[BOJ/12771]

Yullgiii·2025년 1월 12일

TIL algorithm

개발자로의 취업을 준비하며 TIL

목록 보기

352/363

TIL: 최대 석유 채굴량 문제 풀이

문제 설명

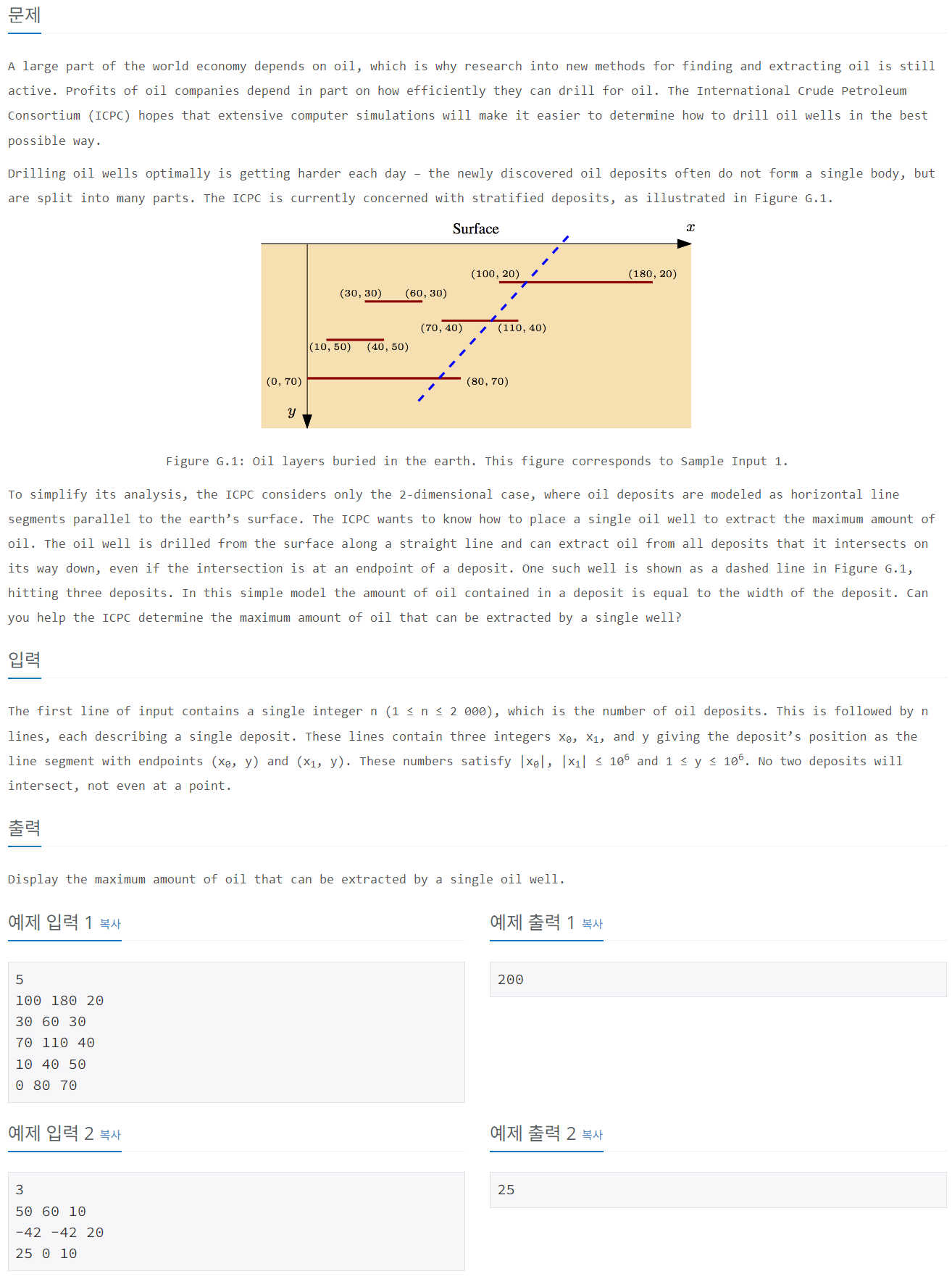
석유 회사들은 효율적인 시추 방법을 찾기 위해 연구 중이다. 이 문제는 2차원 공간에서 석유층을 수평선분으로 모델링하고, 하나의 시추공을 통해 얻을 수 있는 최대 석유량을 계산하는 것이다.

시추공은 직선으로 지표면에서 수직으로 뚫는다.
시추공이 지나가는 모든 석유층의 너비만큼 석유를 채굴할 수 있다.
석유층은 겹치지 않으며, 수평으로 놓여있다.

입력

첫 번째 줄: 석유층의 수 n (1 ≤ n ≤ 2000)
이후 n개의 줄: 각 석유층의 좌표 ((x_0, x_1, y))
- (|x_0|, |x_1| ≤ 10^6)
- (1 ≤ y ≤ 10^6)

출력

최대 석유 채굴량을 출력한다.

예제 입력 1

5 100 180 20 30 60 30 70 110 40 10 40 50 0 80 70

예제 출력 1

문제 풀이 방법

1. 핵심 아이디어

석유층을 선분으로 모델링하고, 시추공을 수직선으로 뚫는다.
시추공이 지나가는 석유층들의 너비를 합산해 최대값을 찾는다.

2. 알고리즘 설계

기준점(Pivot)을 설정해 모든 석유층의 끝점을 기울기 기준으로 정렬.
CCW(Counter Clock Wise)를 이용해 기울기 방향을 정렬한다.
석유층이 시추공을 만났는지 확인하며 석유량을 누적한다.

코드

import java.util.*;

public class Main {
    static class Pos implements Comparable<Pos> {
        long x, y, size;
        int index;

        Pos(long x, long y, int index, long size) {
            this.x = x;
            this.y = y;
            this.size = size;
            this.index = index;
        }

        // 기준점에 대해 벡터로 변환
        Pos moveByPivot(Pos p) {
            if (this.y < p.y) {
                return new Pos(p.x - this.x, p.y - this.y, index, size);
            }
            return new Pos(this.x - p.x, this.y - p.y, index, size);
        }

        // CCW를 이용해 방향성 비교
        long ccw(Pos p) {
            return this.x * p.y - this.y * p.x;
        }

        @Override
        public int compareTo(Pos p) {
            long tmp = this.ccw(p);
            if (tmp == 0) {
                return Long.compare(p.size, this.size);
            }
            return Long.compare(tmp, 0);
        }
    }

    static int n;
    static Pos[] pos;

    // 특정 기준점에서 최대 석유량 계산
    static long makePivot(Pos pivot) {
        List<Pos> ps = new ArrayList<>();
        for (Pos p : pos) {
            Pos mp = p.moveByPivot(pivot);
            if (mp.y > 0) {
                ps.add(mp);
            }
        }

        Collections.sort(ps);
        boolean[] met = new boolean[n];

        // 석유층이 중복으로 더해지지 않도록 체크
        for (Pos p : ps) {
            if (met[p.index]) {
                p.size *= -1;  // 중복된 석유층은 빼준다.
            } else {
                met[p.index] = true;
            }
        }

        Collections.sort(ps);

        long ans = pivot.size, sum = pivot.size;
        for (Pos p : ps) {
            sum += p.size;
            ans = Math.max(ans, sum);
        }
        return ans;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        pos = new Pos[n * 2];

        for (int i = 0; i < n; i++) {
            long x0 = sc.nextLong();
            long x1 = sc.nextLong();
            long y = sc.nextLong();
            long size = Math.abs(x1 - x0);
            pos[i * 2] = new Pos(x0, y, i, size);   // 시작점
            pos[i * 2 + 1] = new Pos(x1, y, i, size); // 끝점
        }

        long result = 0;
        for (Pos p : pos) {
            result = Math.max(result, makePivot(p));
        }
        System.out.println(result);
    }
}

코드 설명

Pos 클래스
- 석유층의 위치와 정보를 저장한다.
- moveByPivot: 기준점을 중심으로 좌표를 변환해 벡터로 변경.
- ccw: 기울기를 계산해 방향성을 판별.
makePivot 함수
- 기준점을 잡고, 그 기준으로 나머지 점들을 기울기 기준으로 정렬.
- 시추공이 지나가는 석유층의 너비를 누적하고 최대값을 계산.
- 중복된 석유층은 음수로 변환해 제외한다.
메인 로직
- 입력받은 석유층 정보를 저장하고, 각 점을 기준으로 최대 석유량을 계산.
- 그 중 최대값을 출력.