1월 14일 - Range GCD[BOJ/12858]

문제 설명

길이 N인 자연수 수열이 주어진다. 이 수열에 대해 두 가지 연산을 효율적으로 처리해야 한다.

1. 구간 덧셈 연산: 수열의 A번째 원소부터 B번째 원소까지 특정 수 T를 더한다.
2. 구간 GCD 연산: 수열의 A번째 원소부터 B번째 원소까지의 최대공약수(GCD)를 구한다.

입력 조건

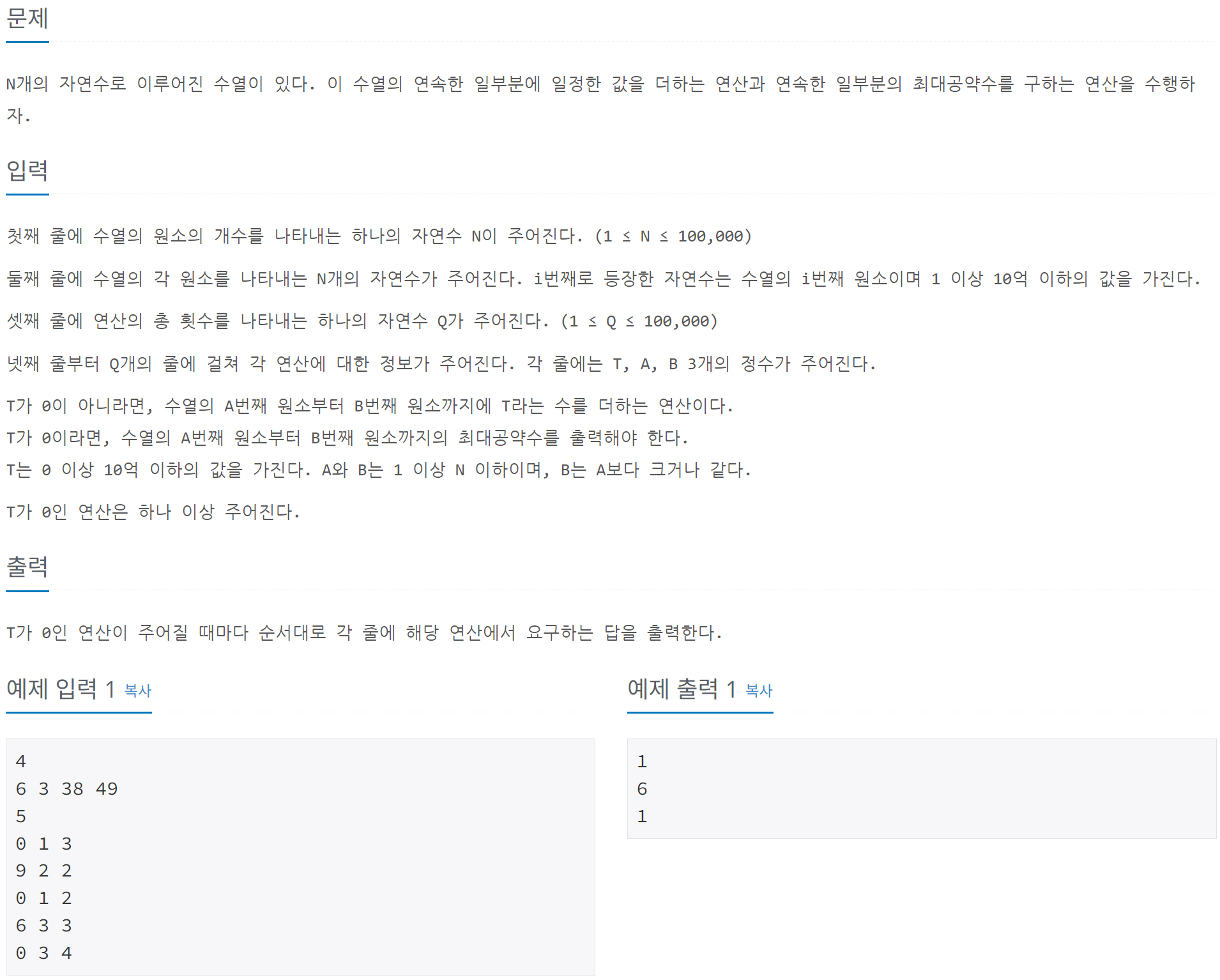
• 수열의 크기 N (1 ≤ N ≤ 100,000)
• 각 원소는 1 이상 10억 이하의 자연수
• 연산의 수 Q (1 ≤ Q ≤ 100,000)
• 연산은 T A B 형식으로 주어짐
  • T > 0: 구간 [A, B]에 T를 더하는 연산
  • T = 0: 구간 [A, B]의 최대공약수 출력

출력

• T = 0인 쿼리마다 결과를 출력

예제 입력 1

4 6 3 38 49 5 0 1 3 9 2 2 0 1 2 6 3 3 0 3 4

예제 출력 1

1 6 1

풀이 전략

1. 구간 덧셈 연산을 효율적으로 처리하기 위해 Lazy Segment Tree를 사용한다.

2. 구간 GCD 연산을 효율적으로 처리하기 위해 Segment Tree를 사용한다.

• 수열의 차분 배열(Difference Array)을 사용해 GCD 연산을 최적화한다.
• GCD 특성상 차분 배열로도 동일한 결과를 얻을 수 있다.
  • ( \text{GCD}(a, b, c) = \text{GCD}(a, |b - a|, |c - b|) )

코드

import java.util.*;

public class Main {
    // Lazy Segment Tree: 구간 덧셈 연산을 빠르게 처리
    static class LazySegmentTree {
        long[] tree, lazy;
        int size;

        public LazySegmentTree(int n) {
            size = 1;
            while (size < n) size <<= 1;
            tree = new long[size << 1];
            lazy = new long[size << 1];
        }

        // Lazy Propagation (구간 업데이트 처리)
        void propagate(int node, int nodeLeft, int nodeRight) {
            if (lazy[node] != 0) {
                tree[node] += (nodeRight - nodeLeft + 1) * lazy[node];
                if (nodeLeft != nodeRight) {
                    lazy[node * 2] += lazy[node];
                    lazy[node * 2 + 1] += lazy[node];
                }
                lazy[node] = 0;
            }
        }

        // 구간 [l, r]에 value 추가
        void update(int l, int r, long value) {
            update(1, 1, size, l, r, value);
        }

        void update(int node, int nodeLeft, int nodeRight, int l, int r, long value) {
            propagate(node, nodeLeft, nodeRight);
            if (r < nodeLeft || nodeRight < l) return;
            if (l <= nodeLeft && nodeRight <= r) {
                lazy[node] += value;
                propagate(node, nodeLeft, nodeRight);
                return;
            }
            int mid = (nodeLeft + nodeRight) >> 1;
            update(node * 2, nodeLeft, mid, l, r, value);
            update(node * 2 + 1, mid + 1, nodeRight, l, r, value);
            tree[node] = tree[node * 2] + tree[node * 2 + 1];
        }

        // 특정 위치 값 조회
        long query(int index) {
            return query(1, 1, size, index);
        }

        long query(int node, int nodeLeft, int nodeRight, int index) {
            propagate(node, nodeLeft, nodeRight);
            if (index < nodeLeft || nodeRight < index) return 0;
            if (nodeLeft == nodeRight) return tree[node];
            int mid = (nodeLeft + nodeRight) >> 1;
            return query(node * 2, nodeLeft, mid, index) + query(node * 2 + 1, mid + 1, nodeRight, index);
        }
    }

    // Segment Tree: GCD 쿼리 처리
    static class SegmentTree {
        long[] tree;
        int size;

        public SegmentTree(int n) {
            size = 1;
            while (size < n) size <<= 1;
            tree = new long[size << 1];
        }

        void update(int index, long value) {
            index += size;
            tree[index] = value;
            while ((index >>= 1) > 0) {
                tree[index] = gcd(tree[index << 1], tree[index << 1 | 1]);
            }
        }

        long query(int l, int r) {
            l += size;
            r += size;
            long res = 0;
            while (l <= r) {
                if ((l & 1) == 1) res = gcd(res, tree[l++]);
                if ((r & 1) == 0) res = gcd(res, tree[r--]);
                l >>= 1;
                r >>= 1;
            }
            return res;
        }

        long gcd(long a, long b) {
            return b == 0 ? a : gcd(b, a % b);
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        LazySegmentTree lazyTree = new LazySegmentTree(n);
        SegmentTree segmentTree = new SegmentTree(n);

        // 초기값 입력 및 차분 배열 생성
        for (int i = 1; i <= n; i++) {
            long value = sc.nextLong();
            lazyTree.update(i, i, value);
        }

        for (int i = 1; i < n; i++) {
            long diff = Math.abs(lazyTree.query(i) - lazyTree.query(i + 1));
            segmentTree.update(i, diff);
        }

        int q = sc.nextInt();
        StringBuilder sb = new StringBuilder();
        while (q-- > 0) {
            int op = sc.nextInt();
            int a = sc.nextInt();
            int b = sc.nextInt();
            if (op == 0) {
                long result = segmentTree.query(a, b - 1);
                result = segmentTree.gcd(result, lazyTree.query(a));
                sb.append(result).append("\n");
            } else {
                lazyTree.update(a, b, op);
                if (a > 1) {
                    long diff = Math.abs(lazyTree.query(a - 1) - lazyTree.query(a));
                    segmentTree.update(a - 1, diff);
                }
                if (b < n) {
                    long diff = Math.abs(lazyTree.query(b) - lazyTree.query(b + 1));
                    segmentTree.update(b, diff);
                }
            }
        }
        System.out.print(sb);
    }
}

So...

이 문제는 구간 덧셈과 구간 GCD 쿼리를 빠르게 처리해야 한다.

• Lazy Segment Tree로 구간 덧셈을 최적화했다.
• Segment Tree로 GCD 쿼리를 효율적으로 처리했다.
• 두 가지 트리를 결합해 문제를 해결했으며, 업데이트와 쿼리가 각각 (O(\log N))으로 효율적이다.