TIL: 안데스 산맥에서 최적의 등반 경로 찾기

문제 설명

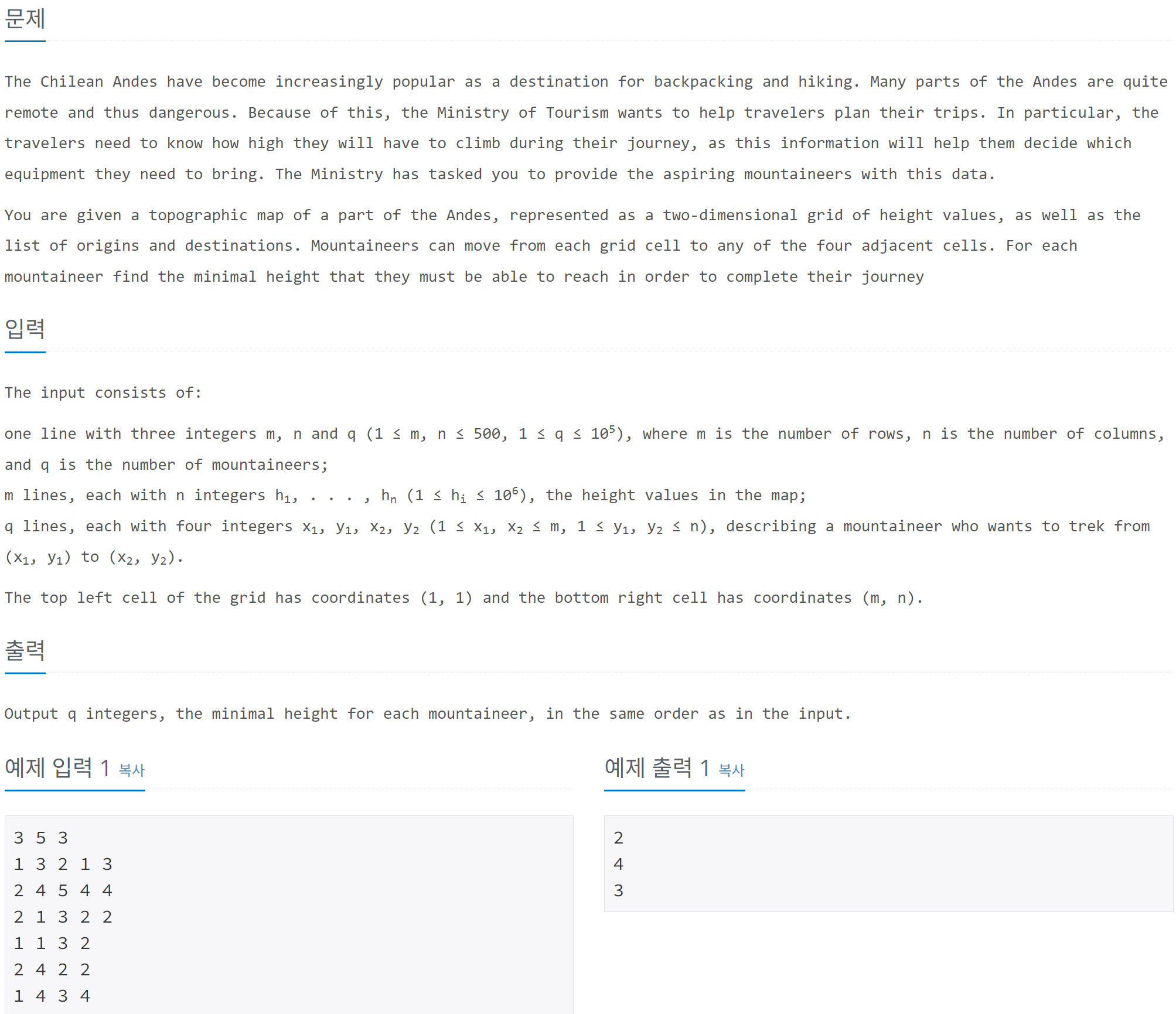
칠레 안데스 산맥에서 등반을 계획하는 등산객들이 이동 경로의 최소 고도를 알고 싶어 한다.
지형은 m x n 크기의 2차원 격자 형태로 주어지며, 각 격자는 고도를 의미한다.

등산객은 네 방향(상, 하, 좌, 우)으로 이동할 수 있다.
각 등산객의 출발지에서 도착지까지 도달하기 위해 반드시 지나야 하는 최소 높이를 구해야 한다.

입력

1. 첫 번째 줄: 세 정수 m, n, q
   • m(행), n(열), q(질문 수)
   • 1 ≤ m, n ≤ 500, 1 ≤ q ≤ 10⁵
2. 다음 m줄: 각 줄마다 n개의 정수(각 격자의 고도)
3. 다음 q줄: 네 정수 (x1, y1, x2, y2) (출발점 → 도착점)

출력

• 각 쿼리에 대해, 출발지에서 도착지까지 갈 수 있는 최소 고도를 출력한다.

문제 접근 방법

1. 이분 탐색 + 유니온 파인드(Disjoint Set Union, DSU) 사용
2. 고도를 기준으로 이분 탐색하면서, 특정 고도 이하의 지점들만 연결
3. 출발점과 도착점이 연결되어 있는지 확인

전체 알고리즘 흐름

1. 모든 고도를 정렬 및 중복 제거
2. 이분 탐색으로 가능한 최소 고도를 탐색
3. 유니온 파인드로 연결 여부 확인

코드

import java.util.*;

public class Main {
    static int[] dx = {0, 0, 1, -1};
    static int[] dy = {1, -1, 0, 0};
    static int N, M, Q;
    static int[] x1, y1, x2, y2, lo, hi, ans;
    static int[][] H;
    static List<Integer>[] mid;
    static List<Cell> d = new ArrayList<>();
    static int[] parent;
    static List<Integer> comp = new ArrayList<>();

    static class Cell implements Comparable<Cell> {
        int height, x, y;

        Cell(int height, int x, int y) {
            this.height = height;
            this.x = x;
            this.y = y;
        }

        @Override
        public int compareTo(Cell o) {
            return Integer.compare(this.height, o.height);
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();
        M = sc.nextInt();
        Q = sc.nextInt();

        H = new int[N + 2][M + 2];
        x1 = new int[Q];
        y1 = new int[Q];
        x2 = new int[Q];
        y2 = new int[Q];
        lo = new int[Q];
        hi = new int[Q];
        ans = new int[Q];
        mid = new ArrayList[1000000];

        for (int i = 0; i < mid.length; i++) mid[i] = new ArrayList<>();

        // 지도 입력 및 고도 저장
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= M; j++) {
                H[i][j] = sc.nextInt();
                comp.add(H[i][j]);
            }
        }

        // 고도 정렬 및 중복 제거
        Collections.sort(comp);
        comp = new ArrayList<>(new LinkedHashSet<>(comp));

        // 고도를 인덱스로 변환
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= M; j++) {
                H[i][j] = Collections.binarySearch(comp, H[i][j]);
                d.add(new Cell(H[i][j], i, j));
            }
        }

        Collections.sort(d);

        // 쿼리 입력
        for (int i = 0; i < Q; i++) {
            x1[i] = sc.nextInt();
            y1[i] = sc.nextInt();
            x2[i] = sc.nextInt();
            y2[i] = sc.nextInt();
            hi[i] = comp.size() - 1;
        }

        // 이분 탐색
        while (true) {
            boolean flag = false;
            for (int i = 0; i < Q; i++) {
                if (lo[i] <= hi[i]) {
                    mid[(lo[i] + hi[i]) / 2].add(i);
                    flag = true;
                }
            }
            if (!flag) break;

            parent = new int[(N + 2) * (M + 2)];
            for (int i = 0; i < parent.length; i++) parent[i] = i;

            for (Cell cell : d) {
                int i = cell.x, j = cell.y;
                for (int k = 0; k < 4; k++) {
                    int ni = i + dx[k], nj = j + dy[k];
                    if (ni >= 1 && ni <= N && nj >= 1 && nj <= M && H[ni][nj] <= cell.height) {
                        union(f(i, j), f(ni, nj));
                    }
                }

                for (int queryIndex : mid[cell.height]) {
                    if (H[x1[queryIndex]][y1[queryIndex]] <= cell.height &&
                        H[x2[queryIndex]][y2[queryIndex]] <= cell.height &&
                        find(f(x1[queryIndex], y1[queryIndex])) == find(f(x2[queryIndex], y2[queryIndex]))) {
                        ans[queryIndex] = cell.height;
                        hi[queryIndex] = cell.height - 1;
                    } else {
                        lo[queryIndex] = cell.height + 1;
                    }
                }
            }

            for (List<Integer> list : mid) list.clear();
        }

        for (int i = 0; i < Q; i++) {
            System.out.println(comp.get(ans[i]));
        }
    }

    static int f(int x, int y) {
        return x * (M + 2) + y;
    }

    static int find(int x) {
        if (parent[x] == x) return x;
        return parent[x] = find(parent[x]);
    }

    static void union(int x, int y) {
        parent[find(x)] = find(y);
    }
}

풀이 과정 상세 설명

1. 입력 처리

   • 고도를 입력받아 comp 리스트에 저장하고 중복 제거 및 정렬.

2. 이분 탐색

   • 쿼리별로 가능한 최소 고도를 이분 탐색을 통해 탐색.

3. 유니온 파인드(DSU)

   • 특정 고도 이하의 격자들만 연결해 출발점과 도착점 연결 여부를 확인.

4. 결과 출력

   • 최적의 고도 결과 출력.

So...

이 문제는 이분 탐색과 유니온 파인드의 결합으로 효율적으로 해결할 수 있다.
고도를 기준으로 이분 탐색하고, 해당 고도 이하의 격자를 연결해 출발점과 도착점 연결 여부를 빠르게 판별했다.
이로써 모든 쿼리를 효율적으로 처리할 수 있었다.

시간 복잡도는 (O(Q \log^2 N))으로, 대규모 입력도 무리 없이 처리 가능했다.