1월 21일 - 루트 노드가 많은 트리일수록 좋은 트리이다 [BOJ/24272]

문제 설명

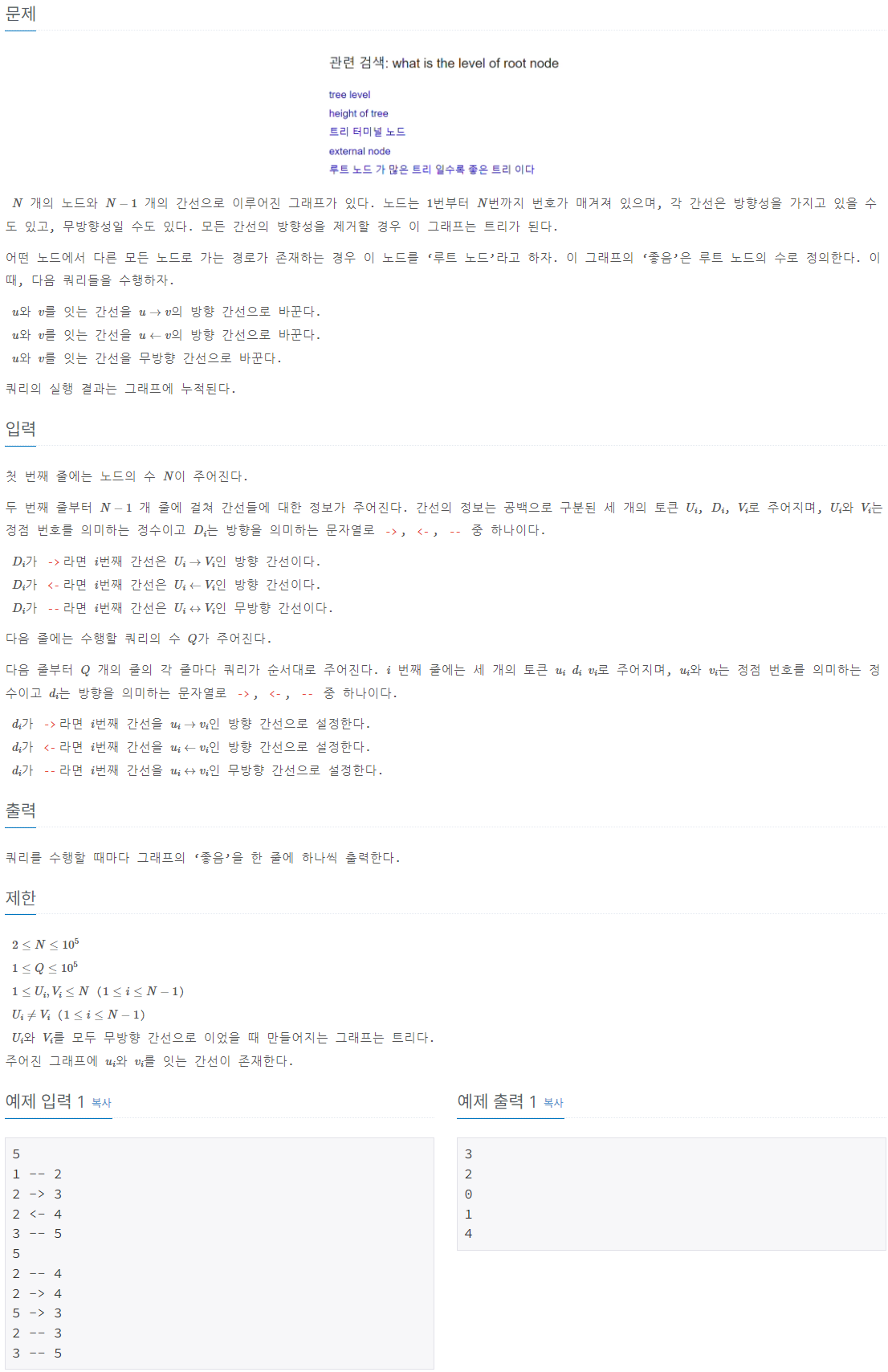
이 문제는 주어진 트리에 방향성을 추가하거나 제거하며, 루트 노드의 개수를 구하는 쿼리를 처리하는 문제이다. 트리는 ( N )개의 노드와 ( N-1 )개의 간선으로 구성되어 있으며, 초기 상태에서 모든 간선은 방향성이 없거나 방향성이 부여되어 있다. 쿼리에서 제공된 간선 방향성 수정 명령에 따라 현재 그래프의 ‘좋음’(루트 노드의 개수)을 계산해야 한다.

해결 방법

핵심 아이디어

1. 서브트리 계산: 트리의 서브트리 크기와 방문 시간을 DFS로 계산하여 간선 방향성에 따라 영향을 받는 노드들을 쉽게 추적한다.
2. 세그먼트 트리 활용: 방향성이 추가/삭제될 때 영향을 받는 구간을 세그먼트 트리로 관리하여 빠르게 루트 노드의 수를 계산한다.
3. 간선 상태 관리: set을 활용하여 현재 간선의 방향성을 저장하고, 쿼리를 처리할 때 상태를 갱신한다.

코드

#include <bits/stdc++.h>
using namespace std;

array<vector<int>, 100001> treeAdj; // 트리의 인접 리스트
array<int, 100001> entryTime, subTreeSize; // 방문 시간과 서브트리 크기

// DFS를 통해 각 노드의 방문 시간과 서브트리 크기 계산
void calculateSubtree(int parent, int current, int& clock) {
    entryTime[current] = clock++;
    subTreeSize[current] = 1;
    for (int neighbor : treeAdj[current]) {
        if (neighbor != parent) {
            calculateSubtree(current, neighbor, clock);
            subTreeSize[current] += subTreeSize[neighbor];
        }
    }
}

// 세그먼트 트리 클래스 정의
class SegmentTree {
    int size;
    vector<int> count, value;

    void updateRange(int node, int nodeStart, int nodeEnd, int rangeStart, int rangeEnd, int delta) {
        int nodeMid = (nodeStart + nodeEnd) >> 1;
        if (nodeStart > rangeEnd || nodeEnd < rangeStart) return;
        if (rangeStart <= nodeStart && nodeEnd <= rangeEnd) {
            count[node] += delta;
        } else {
            updateRange(node << 1, nodeStart, nodeMid, rangeStart, rangeEnd, delta);
            updateRange(node << 1 | 1, nodeMid + 1, nodeEnd, rangeStart, rangeEnd, delta);
        }
        if (count[node]) value[node] = nodeEnd - nodeStart + 1;
        else if (nodeStart != nodeEnd) value[node] = value[node << 1] + value[node << 1 | 1];
        else value[node] = 0;
    }

public:
    SegmentTree(int n) {
        size = 1;
        while (size < n) size *= 2;
        count.resize(size * 2);
        value.resize(size * 2);
    }

    void update(int rangeStart, int rangeEnd, int delta) {
        if (rangeStart > rangeEnd) return;
        updateRange(1, 0, size - 1, rangeStart, rangeEnd, delta);
    }

    int query() { return value[1]; }
};

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(0);

    int nodeCount;
    cin >> nodeCount;

    vector<pair<int, int>> directedEdges;
    for (int i = 1; i < nodeCount; ++i) {
        int u, v;
        string direction;
        cin >> u >> direction >> v;
        treeAdj[u].emplace_back(v);
        treeAdj[v].emplace_back(u);
        if (direction[0] == '<') directedEdges.emplace_back(v, u);
        if (direction[1] == '>') directedEdges.emplace_back(u, v);
    }

    int clock = 0;
    calculateSubtree(0, 1, clock);

    SegmentTree segmentTree(nodeCount);
    set<pair<int, int>> edgeSet;

    for (const auto& [x, y] : directedEdges) {
        if (subTreeSize[x] > subTreeSize[y]) segmentTree.update(entryTime[y], entryTime[y] + subTreeSize[y] - 1, 1);
        else {
            segmentTree.update(0, entryTime[x] - 1, 1);
            segmentTree.update(entryTime[x] + subTreeSize[x], nodeCount - 1, 1);
        }
        edgeSet.emplace(x, y);
    }

    int queryCount;
    cin >> queryCount;
    while (queryCount--) {
        int u, v;
        string direction;
        cin >> u >> direction >> v;

        if (edgeSet.find({u, v}) != edgeSet.end()) {
            if (subTreeSize[u] > subTreeSize[v]) segmentTree.update(entryTime[v], entryTime[v] + subTreeSize[v] - 1, -1);
            else {
                segmentTree.update(0, entryTime[u] - 1, -1);
                segmentTree.update(entryTime[u] + subTreeSize[u], nodeCount - 1, -1);
            }
            edgeSet.erase({u, v});
        } else if (edgeSet.find({v, u}) != edgeSet.end()) {
            if (subTreeSize[v] > subTreeSize[u]) segmentTree.update(entryTime[u], entryTime[u] + subTreeSize[u] - 1, -1);
            else {
                segmentTree.update(0, entryTime[v] - 1, -1);
                segmentTree.update(entryTime[v] + subTreeSize[v], nodeCount - 1, -1);
            }
            edgeSet.erase({v, u});
        }

        if (direction.compare("--")) {
            if (direction[0] == '<') swap(u, v);
            if (subTreeSize[u] > subTreeSize[v]) segmentTree.update(entryTime[v], entryTime[v] + subTreeSize[v] - 1, 1);
            else {
                segmentTree.update(0, entryTime[u] - 1, 1);
                segmentTree.update(entryTime[u] + subTreeSize[u], nodeCount - 1, 1);
            }
            edgeSet.emplace(u, v);
        }
        cout << nodeCount - segmentTree.query() << '\n';
    }

    return 0;
}

코드설명

1. DFS 초기화:

• calculateSubtree를 이용해 트리의 각 노드에 대해 방문 시간과 서브트리 크기를 계산한다.

2. 세그먼트 트리 업데이트:

• 방향성 추가/제거 시 영향을 받는 구간을 세그먼트 트리에서 업데이트한다.

3. 간선 상태 관리:

• set을 사용해 현재 간선의 방향성을 저장하고, 쿼리에 따라 추가/삭제를 수행한다.

So...

이 문제는 DFS로 트리의 서브트리를 계산하고, 세그먼트 트리를 사용하여 효율적으로 루트 노드의 개수를 관리하는 것이 핵심이다.
특히, 쿼리당 복잡도를 (O(\log N))로 유지하여 대규모 입력에서도 빠르게 처리할 수 있었다.

이번 문제를 통해 트리 탐색과 세그먼트 트리의 결합이라는 강력한 기법을 학습할 수 있었다.
이러한 접근은 동적 그래프와 관련된 문제에서도 매우 유용하다.