TIL: Strike Zone Optimization - Using Segment Tree for Maximum Evaluation

문제 설명

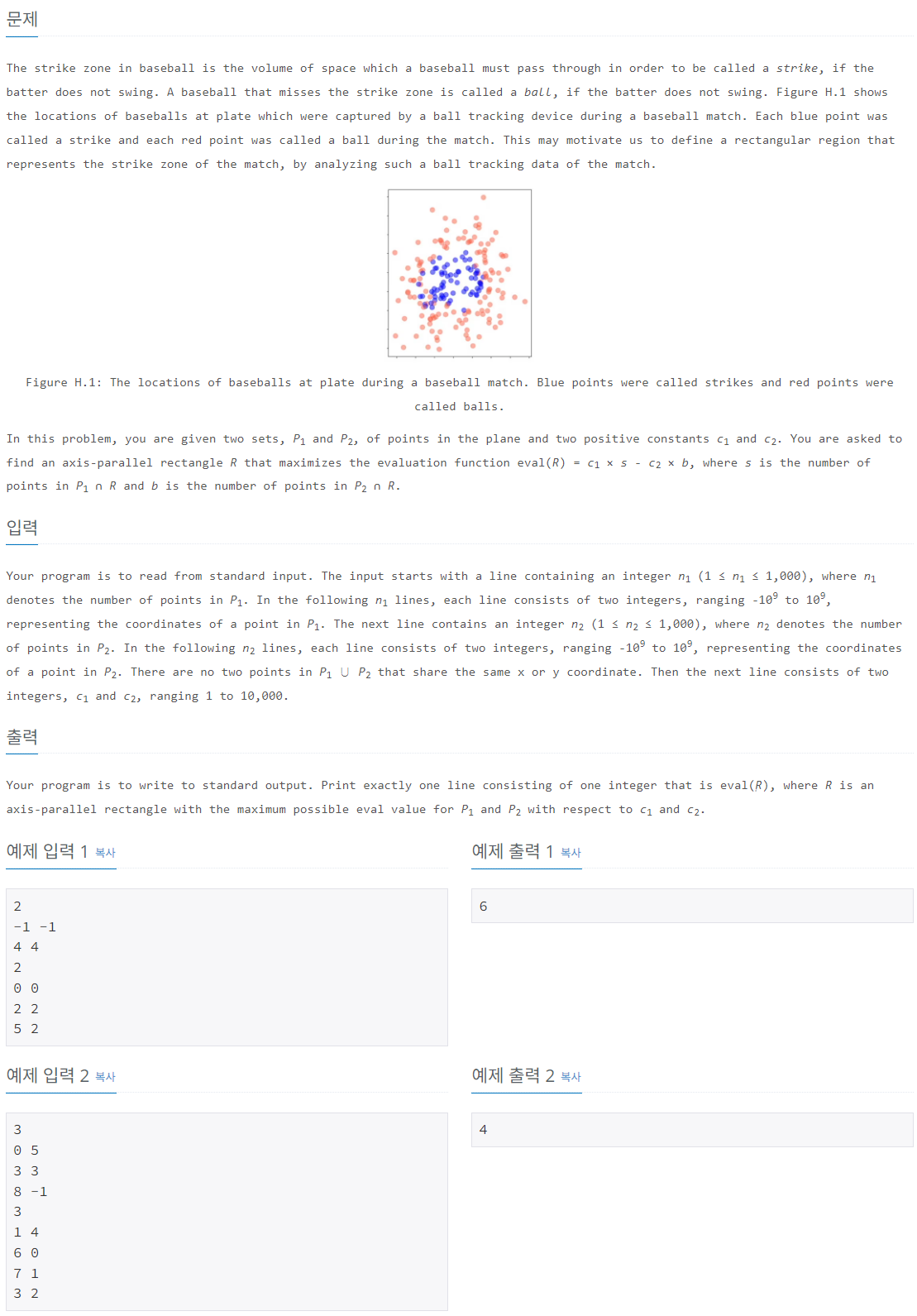
Strike Zone Optimization 문제는 특정 공간 내의 데이터를 분석하여 직사각형 ( R )의 최적 영역을 찾는 것이다. 주어진 두 점 집합 ( P1 ) (strike)과 ( P2 ) (ball)에 대해, 다음 평가 함수 ( \text{eval}(R) )를 최대화하는 직사각형 ( R )을 구하는 것이 목표다:
[
\text{eval}(R) = c1 \times s - c2 \times b
]
여기서:

• ( s ): ( R ) 내부에 있는 ( P1 )의 점 개수
• ( b ): ( R ) 내부에 있는 ( P2 )의 점 개수
• ( c1 ), ( c2 ): 주어진 가중치

문제 해결 접근

핵심 아이디어

1. 좌표 압축: 좌표의 범위가 매우 크므로, 좌표 압축으로 메모리를 최적화한다.
2. 세그먼트 트리 활용: 직사각형 ( R )의 위/아래 범위를 이동하면서 x축 방향을 스캔하고 최적의 평가 값을 구한다.
3. 좌표 스윕: y축 기준으로 스윕하며 x축 범위의 값을 세그먼트 트리에 업데이트하여, 모든 가능한 직사각형에 대한 평가 값을 계산한다.

코드

#include <bits/stdc++.h>
using namespace std;

// 세그먼트 트리의 노드 구조체 정의
struct TreeNode {
    long long sum, maxVal, leftMax, rightMax;
    TreeNode() : sum(0), maxVal(0), leftMax(0), rightMax(0) { }
    
    // 두 노드를 합치는 연산 정의
    TreeNode operator+(TreeNode &other) {
        TreeNode result;
        result.sum = sum + other.sum;
        result.leftMax = max(leftMax, sum + other.leftMax);
        result.rightMax = max(other.rightMax, rightMax + other.sum);
        result.maxVal = max(rightMax + other.leftMax, max(maxVal, other.maxVal));
        return result;
    }
};

// 세그먼트 트리 클래스 정의
struct RangeSegmentTree {
    vector<TreeNode> nodes;
    int size;

    RangeSegmentTree(int n) {
        int power = 1;
        while (power < n) power *= 2;
        nodes.resize(power * 2);
        size = power;
    }

    void reset() {
        nodes.clear();
        nodes.resize(size * 2);
    }

    void update(int index, long long value) {
        int current = index + size - 1;
        nodes[current].sum += value;
        nodes[current].leftMax += value;
        nodes[current].rightMax += value;
        nodes[current].maxVal += value;
        while (current > 0) {
            current = (current - 1) / 2;
            nodes[current] = nodes[current * 2 + 1] + nodes[current * 2 + 2];
        }
    }

    long long queryMax(int left, int right) {
        left += size;
        right += size + 1;
        TreeNode leftResult, rightResult;
        while (left < right) {
            if (right & 1) {
                --right;
                rightResult = nodes[right - 1] + rightResult;
            }
            if (left & 1) {
                leftResult = leftResult + nodes[left - 1];
                ++left;
            }
            left >>= 1;
            right >>= 1;
        }
        return (leftResult + rightResult).maxVal;
    }
};

// 좌표와 가중치를 저장하는 구조체 정의
struct Coordinate {
    int x, y; long long weight;
    Coordinate(int x, int y, long long weight) : x(x), y(y), weight(weight) { }
    bool operator<(Coordinate &other) {
        return y < other.y;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    vector<Coordinate> coordinates;
    set<int> xCoords, yCoords;
    unordered_map<int, int> xIndex, yIndex;

    // P1 입력
    int positiveCount;
    cin >> positiveCount;
    for (int i = 0; i < positiveCount; i++) {
        int x, y;
        cin >> x >> y;
        xCoords.insert(x);
        yCoords.insert(y);
        coordinates.emplace_back(x, y, 1);
    }

    // P2 입력
    int negativeCount;
    cin >> negativeCount;
    for (int i = 0; i < negativeCount; i++) {
        int x, y;
        cin >> x >> y;
        xCoords.insert(x);
        yCoords.insert(y);
        coordinates.emplace_back(x, y, -1);
    }

    // 가중치 입력
    long long weightPositive, weightNegative;
    cin >> weightPositive >> weightNegative;

    // 좌표 압축
    int index = 0;
    for (const auto& x : xCoords) xIndex[x] = index++;
    index = 0;
    for (const auto& y : yCoords) yIndex[y] = index++;

    int xSize = xCoords.size();
    int ySize = yCoords.size();
    RangeSegmentTree segmentTree(xSize);

    // 좌표 스윕 및 세그먼트 트리 계산
    sort(coordinates.begin(), coordinates.end());
    long long maximumValue = LLONG_MIN;
    for (int i = 0; i < ySize; i++) {
        segmentTree.reset();
        for (const auto& point : coordinates) {
            if (yIndex[point.y] < i) continue;
            long long weight = (point.weight == 1 ? weightPositive : -weightNegative);
            segmentTree.update(xIndex[point.x], weight);
            maximumValue = max(maximumValue, segmentTree.queryMax(0, xSize - 1));
        }
    }
    cout << maximumValue << '\n';
}

코드 풀이

1. 좌표 압축 및 데이터 준비

   • 모든 좌표 (x, y)를 압축하여 연속적 인덱스로 매핑한다.
   • (P1)과 (P2)의 점을 모두 단일 배열로 관리한다.

2. 세그먼트 트리 초기화 및 업데이트

   • (x)-좌표를 기준으로 세그먼트 트리를 생성한다.
   • 점의 (x)-좌표를 기준으로 세그먼트 트리를 업데이트하여 각 (y)-라인별 최대 평가 값을 계산한다.

3. (y)축 스윕 및 최대값 계산

   • 각 (y)-라인을 기준으로 (x)-범위를 탐색하며 (eval(R))를 계산한다.

So...

이 문제는 세그먼트 트리와 좌표 압축을 결합해 효율적으로 해결했다.
핵심은 2차원 좌표 공간에서 선형 시간 복잡도를 유지하며 최적의 평가 값을 찾는 것이다.

학습한 점:

• 세그먼트 트리를 활용한 구간 최대값 쿼리 구현
• 2D 문제를 1D 문제로 축소하는 좌표 압축 기법

이 접근 방식은 데이터 분석 및 최적화 문제에서도 응용 가능성이 크다.