최대 분리 부메랑 문제

문제 설명

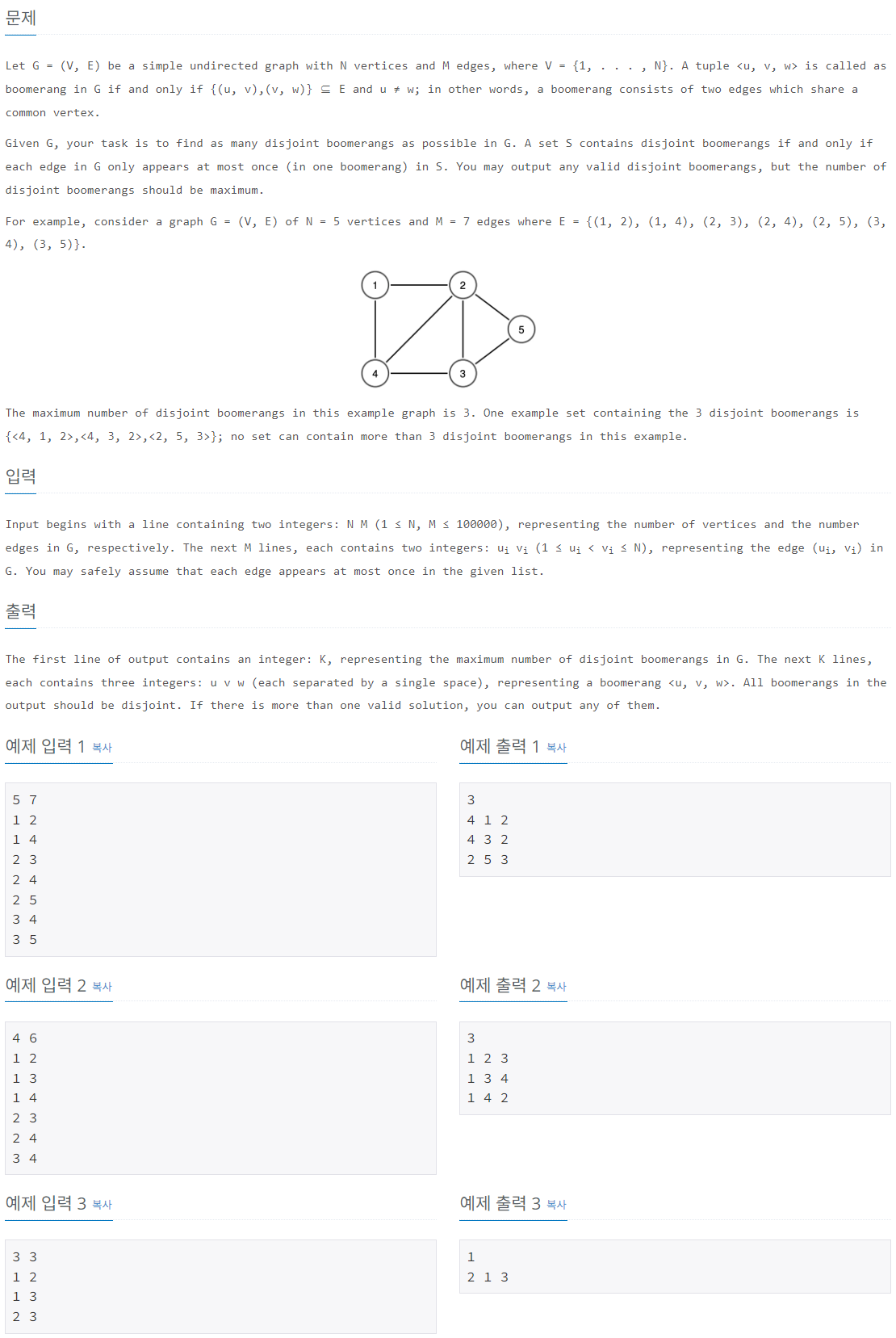
주어진 그래프 ( G = (V, E) )에서 "부메랑"이란 특정 정점 ( v )와 이웃한 두 정점 ( u ), ( w )가 존재하여 ( (u, v) )와 ( (v, w) ) 간선이 있는 구조를 의미한다. ( u \neq w )여야 하며, 각 간선은 오직 하나의 부메랑에만 포함될 수 있다. 목표는 그래프에서 가능한 최대 개수의 분리된 부메랑을 찾는 것이다.

접근 방식

1. DFS로 사이클 탐지 및 처리:

   • 그래프에서 간선이 연결된 구조를 탐색하여 부메랑 조건을 만족하는 세 노드 ( (u, v, w) )를 찾는다.
   • 방문 노드를 관리하여 중복 방문을 방지하며, 간선이 여러 부메랑에 포함되지 않도록 한다.

2. 자식 간선 그룹화:

   • 한 노드에 연결된 자식 노드들을 쌍으로 묶어 가능한 부메랑을 생성한다.
   • 자식 노드가 홀수 개일 경우, 부모 노드와 함께 묶어 부메랑을 만든다.

3. 최적화:

   • 모든 노드를 방문하며 DFS를 수행한다.
   • 노드 방문 여부와 완료 여부를 저장해 불필요한 재탐색을 방지한다.

코드

#include <cstdio>
#include <vector>
using namespace std;

// 사이클을 처리하기 위한 구조체
struct Cycle {
    int start, mid, end;
};

// 노드 수와 간선 수
int numNodes, numEdges;
// 인접 리스트
vector<int> graph[100001];
// 방문 여부와 탐색 종료 여부
bool visited[100001];
bool completed[100001];
// 결과를 저장할 벡터
vector<Cycle> cycles;

// DFS를 수행하여 사이클을 처리하는 함수
bool performDFS(int currentNode, int parentNode) {
    vector<int> children;
    visited[currentNode] = true;

    // 인접 노드 탐색
    for (int neighbor : graph[currentNode]) {
        if (neighbor == parentNode) continue; // 부모 노드는 건너뜀
        if (visited[neighbor]) {
            if (!completed[neighbor]) {
                // 아직 완료되지 않은 노드는 사이클의 일부로 간주
                children.push_back(neighbor);
            }
        } else if (!performDFS(neighbor, currentNode)) {
            // DFS 결과를 기반으로 자식 노드 추가
            children.push_back(neighbor);
        }
    }

    completed[currentNode] = true;

    // 자식 노드 쌍을 처리
    for (int i = 1; i < children.size(); i += 2) {
        cycles.push_back({children[i - 1], currentNode, children[i]});
    }

    // 홀수 개의 자식 노드가 남으면 부모 노드와 함께 처리
    if ((children.size() & 1) && parentNode) {
        cycles.push_back({children.back(), currentNode, parentNode});
        return true;
    }
    return false;
}

int main() {
    // 입력 처리
    scanf("%d%d", &numNodes, &numEdges);
    for (int i = 0; i < numEdges; i++) {
        int node1, node2;
        scanf("%d%d", &node1, &node2);
        graph[node1].emplace_back(node2);
        graph[node2].emplace_back(node1);
    }

    // 모든 노드에 대해 DFS 수행
    for (int i = 1; i <= numNodes; i++) {
        if (!visited[i]) {
            performDFS(i, 0);
        }
    }

    // 결과 출력
    printf("%lu\n", cycles.size());
    for (auto &cycle : cycles) {
        printf("%d %d %d\n", cycle.start, cycle.mid, cycle.end);
    }
}

코드 설명

1. 입력 처리:

   • 간선 정보를 받아 각 노드의 인접 리스트를 생성한다.

2. DFS를 통한 사이클 탐지:

   • performDFS 함수는 현재 노드와 부모 노드를 기반으로 인접 노드를 탐색하며 부메랑을 구성한다.
   • 방문된 노드 중 완료되지 않은 노드는 자식으로 간주한다.

3. 부메랑 생성:

   • 자식 노드가 짝수 개일 경우, 두 개씩 묶어 부메랑 생성.
   • 홀수 개일 경우, 부모 노드를 포함하여 마지막 남은 노드를 처리.

4. 결과 출력:

   • 최대 개수의 분리된 부메랑과 해당 부메랑의 노드 정보를 출력.

So...

이 접근법은 DFS를 사용해 그래프를 효율적으로 탐색하며, 각 간선을 오직 하나의 부메랑에만 포함되도록 보장한다. 그래프의 구조에 따라 다양한 부메랑 집합이 생성될 수 있으므로, 최대 개수의 부메랑을 찾는 데 최적화되어 있다. 결과적으로, 이 방법은 입력 크기가 커도 효과적으로 작동하며, 문제 요구 조건을 충족한다.