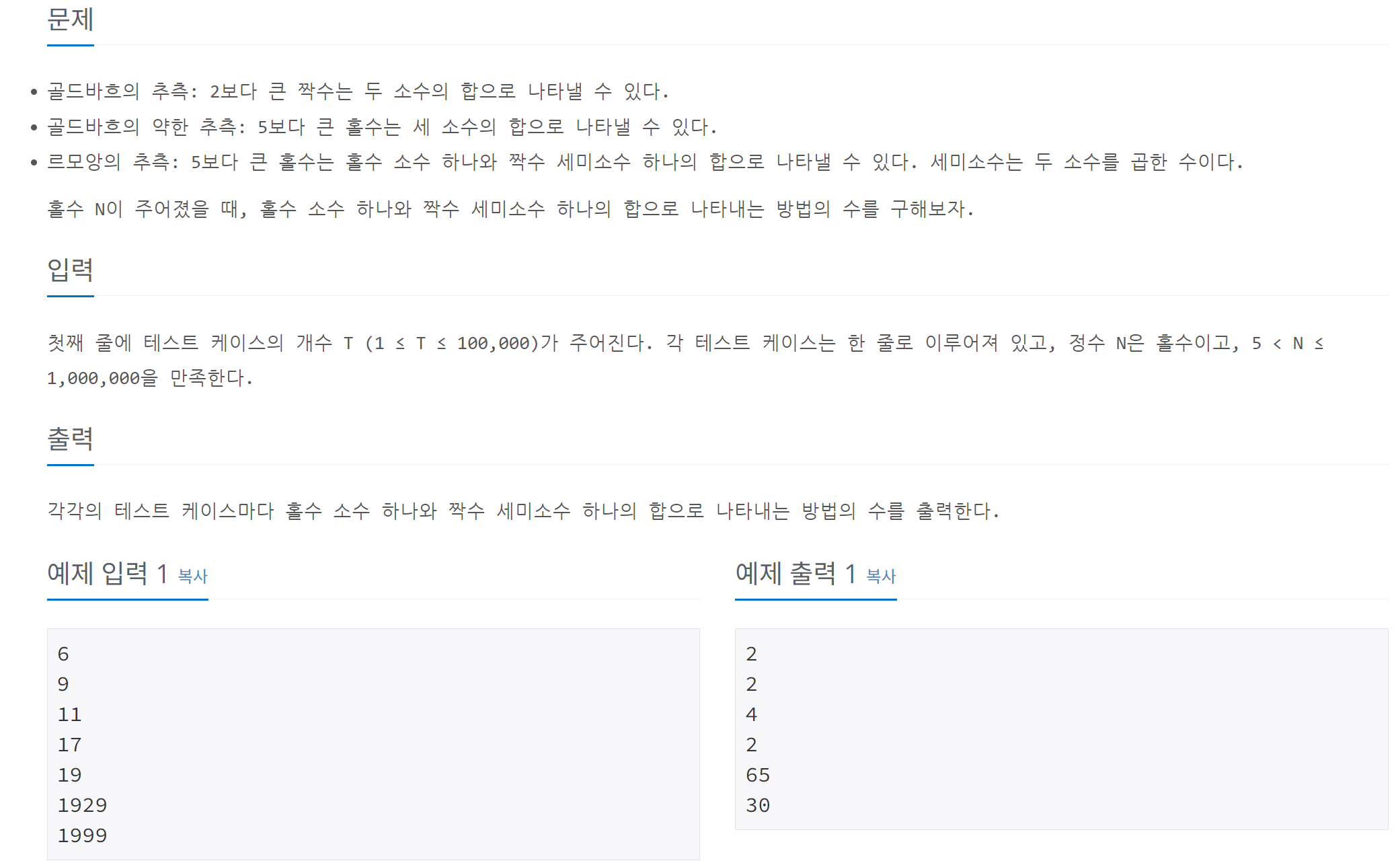
골드바흐의 약한 추측 응용 문제: 홀수 소수와 짝수 세미소수의 합

문제 설명

골드바흐의 약한 추측은 "5보다 큰 홀수는 세 소수의 합으로 표현 가능하다"고 한다. 이 문제는 이를 확장하여, "5보다 큰 홀수를 홀수 소수와 짝수 세미소수의 합으로 표현할 수 있는 모든 방법의 수를 구하라"는 것이다.

여기서:

• 홀수 소수는 홀수이면서 소수인 숫자이다.
• 짝수 세미소수는 두 소수의 곱으로 표현되는 짝수이다.

접근 방식

1. 에라토스테네스의 체로 소수 계산:

   • 1,000,000 이하의 소수를 계산하여 소수 배열 isPrime을 생성한다.

2. 홀수 소수와 짝수 세미소수 추출:

   • oddPrimes 배열에 홀수 소수를, semiPrimes 배열에 짝수 세미소수를 저장한다.

3. FFT를 이용한 빠른 다항식 곱셈:

   • 홀수 소수와 짝수 세미소수를 표현하는 두 배열의 곱셈을 수행하여, 각 수를 표현할 수 있는 조합 수를 계산한다.

4. 결과 출력:

   • 테스트 케이스에 따라 결과 배열에서 각 입력값에 해당하는 조합 수를 출력한다.

코드

#include <iostream>
#include <complex>
#include <vector>
#include <cstring>
#include <string>
#include <algorithm>

using namespace std;
typedef complex<double> Complex;
typedef long long ll;
const double PI = acos(-1);

// FFT 구현 함수
void performFFT(vector<Complex>& data, bool inverse = false) {
    int size = data.size(), index = 0;
    vector<Complex> roots(size / 2);

    // 데이터 재배치 (비트 반전)
    for (int i = 1; i < size; i++) {
        int bit = size >> 1;
        while (index >= bit) {
            index -= bit;
            bit >>= 1;
        }
        index += bit;
        if (i < index) swap(data[i], data[index]);
    }

    // 복소수 각도 계산
    double angle = 2 * PI / size * (inverse ? -1 : 1);
    for (int i = 0; i < size / 2; i++) {
        roots[i] = Complex(cos(angle * i), sin(angle * i));
    }

    // FFT 수행 (분할 정복)
    for (int len = 2; len <= size; len <<= 1) {
        int step = size / len;
        for (int i = 0; i < size; i += len) {
            for (int j = 0; j < len / 2; j++) {
                Complex u = data[i + j];
                Complex v = data[i + j + len / 2] * roots[step * j];
                data[i + j] = u + v;
                data[i + j + len / 2] = u - v;
            }
        }
    }

    // 역변환 시 정규화
    if (inverse) {
        for (int i = 0; i < size; i++) data[i] /= size;
    }
}

// 두 벡터의 곱셈 연산 (FFT 이용)
vector<ll> multiplyPolynomials(vector<ll>& poly1, vector<ll>& poly2) {
    vector<Complex> comp1(poly1.begin(), poly1.end()), comp2(poly2.begin(), poly2.end());

    // 벡터 크기를 2의 제곱수로 조정
    int n = 2;
    while (n < poly1.size() + poly2.size()) n <<= 1;
    comp1.resize(n);
    comp2.resize(n);

    // FFT 적용
    performFFT(comp1, false);
    performFFT(comp2, false);

    // 요소별 곱
    for (int i = 0; i < n; i++) comp1[i] *= comp2[i];

    // 역 FFT
    performFFT(comp1, true);

    // 결과 저장
    vector<ll> result(n);
    for (int i = 0; i < n; i++) result[i] = (ll)round(comp1[i].real());
    return result;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    // 소수 판별 배열 초기화
    bool isPrime[1000004];
    memset(isPrime, true, sizeof(isPrime));

    // 에라토스테네스의 체로 소수 계산
    for (int i = 2; i <= 1000000; i++) {
        if (isPrime[i]) {
            for (int j = 2; i * j <= 1000000; j++) {
                isPrime[i * j] = false;
            }
        }
    }

    // 홀수 소수 및 세미소수 배열 생성
    vector<ll> oddPrimes(1000004), semiPrimes(1000004);
    for (int i = 2; i <= 1000000; i++) {
        if (isPrime[i]) {
            if (i * 2 <= 1000000) semiPrimes[i * 2] = 1; // 세미소수 저장
            if (i % 2 == 1) oddPrimes[i] = 1; // 홀수 소수 저장
        }
    }

    // FFT를 이용한 다항식 곱셈 수행
    vector<ll> result = multiplyPolynomials(oddPrimes, semiPrimes);

    // 결과값 출력
    int testCases, query;
    cin >> testCases;
    while (testCases--) {
        cin >> query;
        cout << result[query] << "\n";
    }

    return 0;
}

코드 설명

1. FFT 구현:

   • 다항식 곱셈을 빠르게 수행하기 위해 FFT를 구현.
   • 입력 크기를 2의 거듭제곱으로 맞춘 후 FFT를 적용.

2. 에라토스테네스의 체:

   • (1,000,000) 이하의 소수를 계산하여 소수 판별 배열을 생성.

3. 홀수 소수 및 세미소수 계산:

   • 홀수 소수를 oddPrimes 배열에 저장.
   • (2 \times p) 형태의 세미소수를 semiPrimes 배열에 저장.

4. 다항식 곱셈:

   • oddPrimes와 semiPrimes의 다항식 곱셈을 수행하여 각 수를 나타낼 수 있는 방법의 수 계산.

5. 결과 출력:

   • 각 테스트 케이스에 대해 결과 배열에서 조합 수를 출력.

So...

이 접근법은 FFT를 활용하여 다항식 곱셈을 효율적으로 수행함으로써 대량의 입력에서도 빠르게 결과를 계산할 수 있다. 이 과정에서 에라토스테네스의 체를 활용해 소수 및 세미소수를 빠르게 구하고, 결과적으로 각 수를 표현하는 조합 수를 계산하였다.