TIL: 최소 비용으로 땅 구매하기

문제 설명

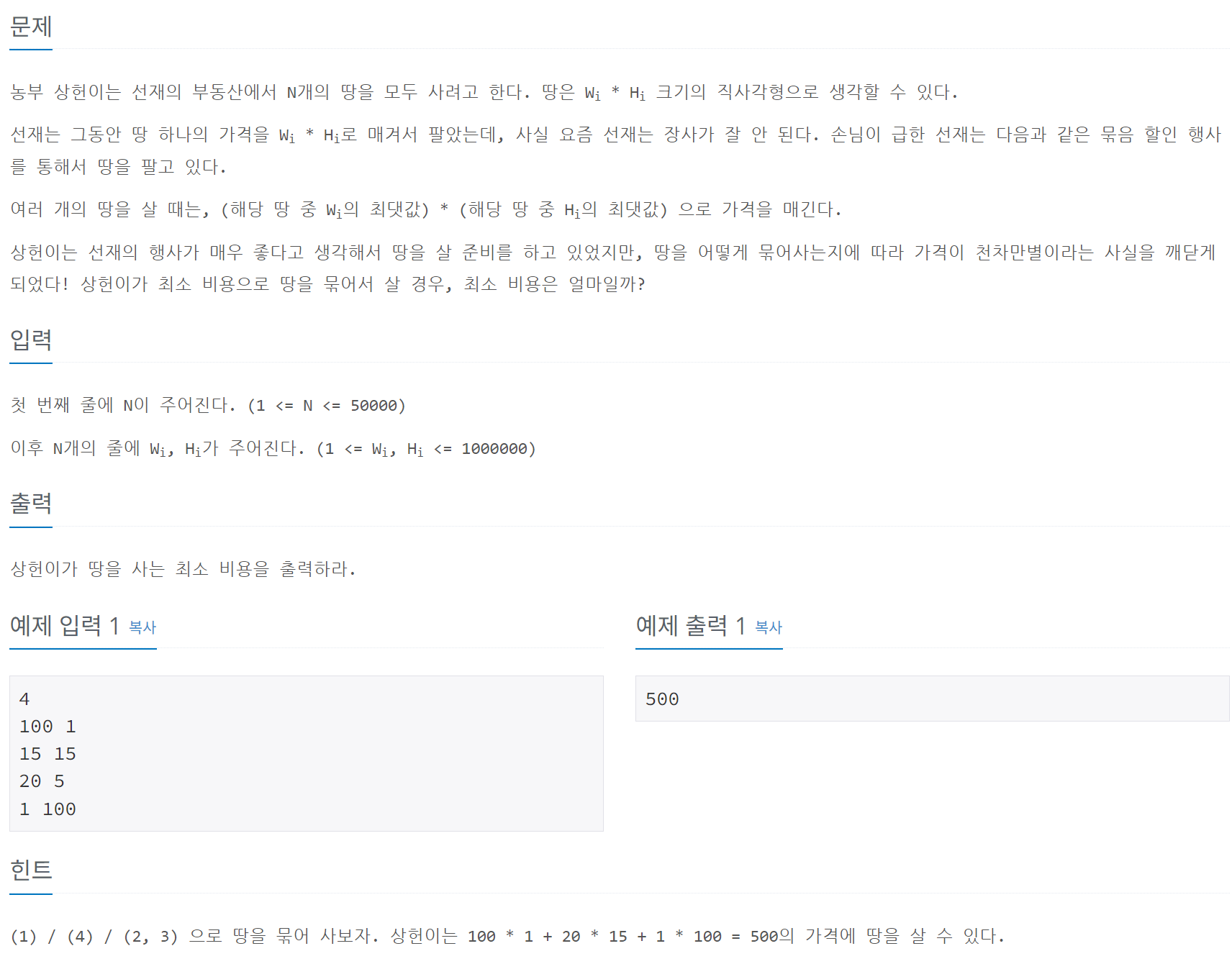
농부 상헌이는 N개의 땅을 구매하려고 한다.
각 땅의 크기는 ( W_i \times H_i )의 직사각형 형태로 표현된다.
선재는 다음과 같은 묶음 할인 정책을 제공한다:

• 묶음 내의 가격은 ((\text{Wi의 최댓값}) \times (\text{Hi의 최댓값})).

이 문제는 상헌이가 땅을 최소 비용으로 묶어 살 수 있도록 하는 방법을 구하는 것이다.

접근 방식

1. 정렬 및 필터링:

   • ( W_i )에 대해 오름차순으로 정렬한 후, 중복되거나 더 작은 ( H_i )를 가지는 항목을 제거하여 유효한 땅 목록만 남긴다.

2. Convex Hull Trick (CHT):

   • 최소 비용을 계산하기 위해 동적 프로그래밍(DP)을 사용한다.
   • DP 점화식:
     [
     \text{dp}[i] = \min_{j < i}(\text{dp}[j] + \text{H}[j] \times \text{W}[i])
     ]
   • CHT를 사용해 (\text{H}[j])와 (\text{dp}[j])를 효율적으로 관리하여 최적의 해를 구한다.

3. 최적화:

   • CHT의 직선 추가 및 질의 과정을 활용해 시간 복잡도를 (\mathcal{O}(N \log N))로 줄인다.

코드

import java.util.*;

public class Main {
    static class Line {
        long m, b; // 기울기와 y절편
        double x; // 이 직선이 다음 직선과 교차하는 x좌표

        Line(long m, long b, double x) {
            this.m = m;
            this.b = b;
            this.x = x;
        }

        long eval(long x) {
            return m * x + b; // 직선 방정식 계산
        }
    }

    static List<Line> lines = new ArrayList<>();
    static int ptr = 0;

    static double intersect(Line a, Line b) {
        return (double) (b.b - a.b) / (a.m - b.m); // 두 직선의 교차점 계산
    }

    static void addLine(long m, long b) {
        Line newLine = new Line(m, b, Double.NEGATIVE_INFINITY);
        while (!lines.isEmpty()) {
            Line last = lines.get(lines.size() - 1);
            double x = intersect(last, newLine);
            if (x <= last.x) {
                lines.remove(lines.size() - 1);
            } else {
                break;
            }
        }
        if (!lines.isEmpty()) {
            newLine.x = intersect(lines.get(lines.size() - 1), newLine);
        }
        lines.add(newLine);
        if (ptr >= lines.size()) ptr = lines.size() - 1;
    }

    static long query(long x) {
        while (ptr < lines.size() - 1 && lines.get(ptr + 1).x < x) {
            ptr++;
        }
        return lines.get(ptr).eval(x);
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        Pair[] lands = new Pair[N];

        for (int i = 0; i < N; i++) {
            long W = sc.nextLong();
            long H = sc.nextLong();
            lands[i] = new Pair(W, H);
        }

        // W 기준으로 정렬
        Arrays.sort(lands, Comparator.comparingLong(p -> p.w));

        // 중복 및 불필요한 땅 제거
        Pair[] filtered = new Pair[N];
        int idx = 0;
        for (Pair land : lands) {
            while (idx > 0 && filtered[idx - 1].h <= land.h) {
                idx--;
            }
            filtered[idx++] = land;
        }

        long[] dp = new long[idx];
        addLine(filtered[0].h, 0); // 첫 번째 직선 추가

        for (int i = 0; i < idx - 1; i++) {
            dp[i] = query(filtered[i].w); // 최적 비용 계산
            addLine(filtered[i + 1].h, dp[i]); // 다음 직선 추가
        }

        System.out.println(query(filtered[idx - 1].w)); // 최종 비용 출력
    }

    static class Pair {
        long w, h;

        Pair(long w, long h) {
            this.w = w;
            this.h = h;
        }
    }
}

풀이 과정

1. 입력 처리 및 정렬:

   • 땅 정보를 입력받아 (W_i)를 기준으로 정렬.
   • (H_i)가 불필요한 경우 제거하여 필터링.

2. Convex Hull Trick 구현:

   • 직선 추가:
     기존 직선들과 교차점을 계산하여 필요 없는 직선 제거.
   • 값 계산:
     주어진 (x)에 대해 최적의 직선을 찾고 값을 계산.

3. DP 및 결과 계산:

   • (dp[i])를 순차적으로 계산하며 직선을 추가.
   • 최종적으로 마지막 땅의 비용 출력.

So...

이 문제는 Convex Hull Trick을 활용하여 동적 프로그래밍을 최적화하는 좋은 예제이다.
문제의 핵심은 "직선 간의 교차점을 효율적으로 관리"하는 데 있었으며, 이를 통해 시간 복잡도를 크게 줄일 수 있었다.
최적화 과정에서 직선 추가와 질의 간의 균형을 맞추는 것이 중요했다.