TIL: 섬 연결 관리 시스템 구현

문제 설명

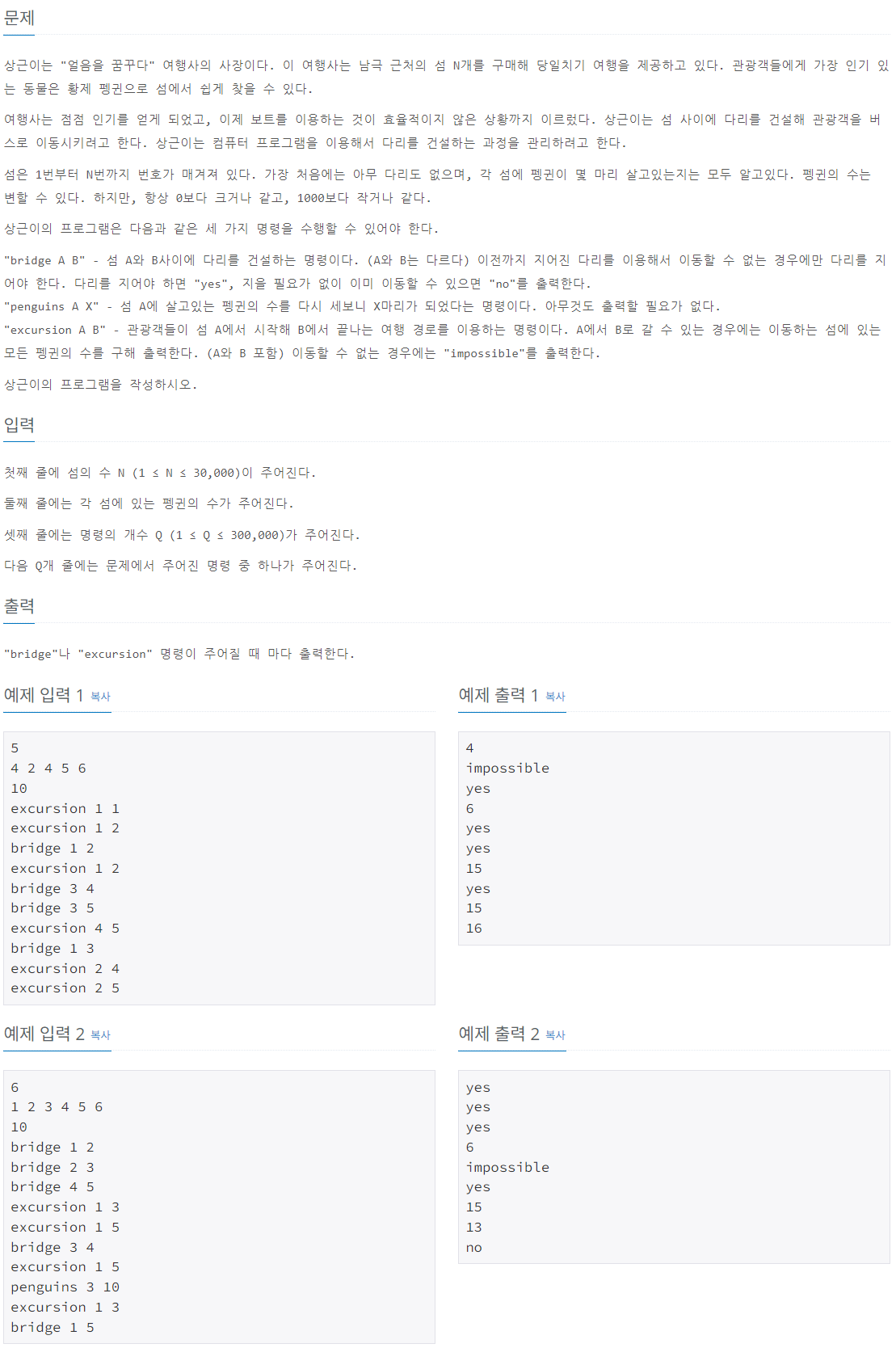
남극 근처의 섬들 간에 다리를 건설해 관광객을 이동시키는 시스템을 구현하는 문제이다.
다음과 같은 세 가지 명령을 처리해야 한다:

1. bridge A B: 섬 A와 B를 연결하는 다리를 건설. 다리가 필요하면 "yes", 이미 연결 가능하면 "no" 출력.
2. penguins A X: 섬 A의 펭귄 수를 X로 변경.
3. excursion A B: 섬 A에서 B로 이동 가능하면 포함된 모든 섬의 펭귄 수의 합 출력. 불가능하면 "impossible" 출력.

접근 방식

1. Union-Find:

   • 섬 간의 연결 관계를 확인하고, 다리가 필요한지 여부를 판단하기 위해 Union-Find를 사용.

2. Heavy-Light Decomposition (HLD):

   • 섬과 연결된 다리의 구조를 트리로 변환하여 펭귄 수의 합을 빠르게 구할 수 있도록 최적화.
   • 체인별로 관리하여 특정 구간의 펭귄 수를 효율적으로 계산.

3. Fenwick Tree:

   • 펭귄 수 업데이트 및 합산을 빠르게 처리하기 위해 사용.

코드

#include <iostream>
#include <string>
#include <vector>
#define ADD_EDGE push_back
#define MAX_NODES 30001
#define MAX_QUERIES 300000

using namespace std;

struct Instruction {
    string type;
    int param1, param2;
    bool result;
} instructions[MAX_QUERIES];

int node_weights[MAX_NODES], subtree_size[MAX_NODES], chain_head[MAX_NODES];
int node_depth[MAX_NODES], parent_node[MAX_NODES], in_time[MAX_NODES], root[MAX_NODES], fenwick_tree[MAX_NODES];
int total_nodes, total_queries, current_time;
vector<int> adjacency_list[MAX_NODES], child_list[MAX_NODES];

// 펜윅 트리 업데이트 함수
void update_fenwick_tree(int idx, int delta) {
    while (idx <= total_nodes) {
        fenwick_tree[idx] += delta;
        idx += idx & -idx;
    }
}

// 펜윅 트리 합 구하기 함수
int query_fenwick_tree(int idx) {
    int sum = 0;
    while (idx) {
        sum += fenwick_tree[idx];
        idx -= idx & -idx;
    }
    return sum;
}

// 체인 내 구간 합 쿼리
int query_range_sum(int node_a, int node_b) {
    int sum = 0;
    while (chain_head[node_a] != chain_head[node_b]) {
        if (node_depth[chain_head[node_a]] < node_depth[chain_head[node_b]])
            swap(node_a, node_b);
        int start = chain_head[node_a];
        sum += query_fenwick_tree(in_time[node_a]) - query_fenwick_tree(in_time[start] - 1);
        node_a = parent_node[start];
    }
    if (node_depth[node_a] > node_depth[node_b])
        swap(node_a, node_b);
    sum += query_fenwick_tree(in_time[node_b]) - query_fenwick_tree(in_time[node_a] - 1);
    return sum;
}

// 유니온-파인드: 루트 노드 찾기
int find_set(int x) {
    if (x == root[x])
        return x;
    return root[x] = find_set(root[x]);
}

// 유니온-파인드: 두 집합 합치기
bool union_set(int node_a, int node_b) {
    node_a = find_set(node_a);
    node_b = find_set(node_b);
    if (node_a != node_b) {
        root[node_a] = node_b;
        return true;
    }
    return false;
}

// DFS를 이용한 트리 초기화
void dfs_initialize(int node) {
    subtree_size[node] = -1;
    for (auto neighbor : adjacency_list[node]) {
        if (subtree_size[neighbor] != 0)
            continue;
        child_list[node].ADD_EDGE(neighbor);
        dfs_initialize(neighbor);
    }
}

// 체인 분할 및 서브트리 크기 계산
void dfs_subtree(int node) {
    subtree_size[node] = 1;
    for (auto &child : child_list[node]) {
        node_depth[child] = node_depth[node] + 1;
        parent_node[child] = node;
        dfs_subtree(child);
        subtree_size[node] += subtree_size[child];
        if (subtree_size[child] > subtree_size[child_list[node][0]])
            swap(child, child_list[node][0]);
    }
}

// 체인 분할 및 노드 인덱스 초기화
void dfs_chain_decomposition(int node) {
    current_time++;
    in_time[node] = current_time;
    for (auto child : child_list[node]) {
        chain_head[child] = (child == child_list[node][0]) ? chain_head[node] : child;
        dfs_chain_decomposition(child);
    }
}

// 초기화 함수
void initialize() {
    cin >> total_nodes;
    for (int i = 1; i <= total_nodes; i++) {
        cin >> node_weights[i];
        root[i] = i;
    }
    cin >> total_queries;
    for (int i = 0; i < total_queries; i++) {
        cin >> instructions[i].type >> instructions[i].param1 >> instructions[i].param2;
        if (instructions[i].type[0] == 'b') {
            instructions[i].result = union_set(instructions[i].param1, instructions[i].param2);
            if (instructions[i].result) {
                adjacency_list[instructions[i].param1].ADD_EDGE(instructions[i].param2);
                adjacency_list[instructions[i].param2].ADD_EDGE(instructions[i].param1);
            }
        }
        if (instructions[i].type[0] == 'e') {
            instructions[i].result = find_set(instructions[i].param1) == find_set(instructions[i].param2);
        }
    }
    dfs_initialize(1);
    dfs_subtree(1);
    dfs_chain_decomposition(1);

    for (int i = 1; i <= total_nodes; i++)
        update_fenwick_tree(in_time[i], node_weights[i]);
}

// 명령 실행 함수
void execute_commands() {
    for (int i = 0; i < total_queries; i++) {
        if (instructions[i].type[0] == 'b')
            cout << (instructions[i].result ? "yes\n" : "no\n");
        if (instructions[i].type[0] == 'p') {
            update_fenwick_tree(in_time[instructions[i].param1], instructions[i].param2 - node_weights[instructions[i].param1]);
            node_weights[instructions[i].param1] = instructions[i].param2;
        }
        if (instructions[i].type[0] == 'e') {
            if (instructions[i].result)
                cout << query_range_sum(instructions[i].param1, instructions[i].param2) << '\n';
            else
                cout << "impossible\n";
        }
    }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    initialize();
    execute_commands();

    return 0;
}

과정 설명

1. 입력 처리:

   • 섬의 개수, 핑권 수, 명령을 입력받는다.

2. Union-Find:

   • 다리를 건설할 때 섬이 이미 연결되었는지 확인하고 연결한다.

3. Heavy-Light Decomposition:

   • 체인으로 나누고, 효율적으로 구간 합 계산을 처리한다.

4. Fenwick Tree:

   • 핑권 수의 변경 및 합산 처리.

5. 명령 처리:

   • 명령 종류에 따라 적절히 Union-Find, Fenwick Tree, HLD를 사용해 결과를 출력한다.

So...

이 문제는 트리 구조, 유니온-파인드, HLD, 펜윅 트리 등 복합적인 알고리즘과 자료구조를 통합적으로 사용하는 문제였다. 특히 효율적 데이터 관리와 업데이트를 요구하는 환경에서, 각 기술을 적절히 배합하여 성능을 극대화할 수 있었다.