[Information Retrieval] 5. Index Compression

hoho·2024년 4월 17일
0

Information Retrieval

목록 보기
6/6

http://cislmu.org 와 학교 수업을 토대로 정리합니다.

1. Recap

Blocked Sort-Based Indexing

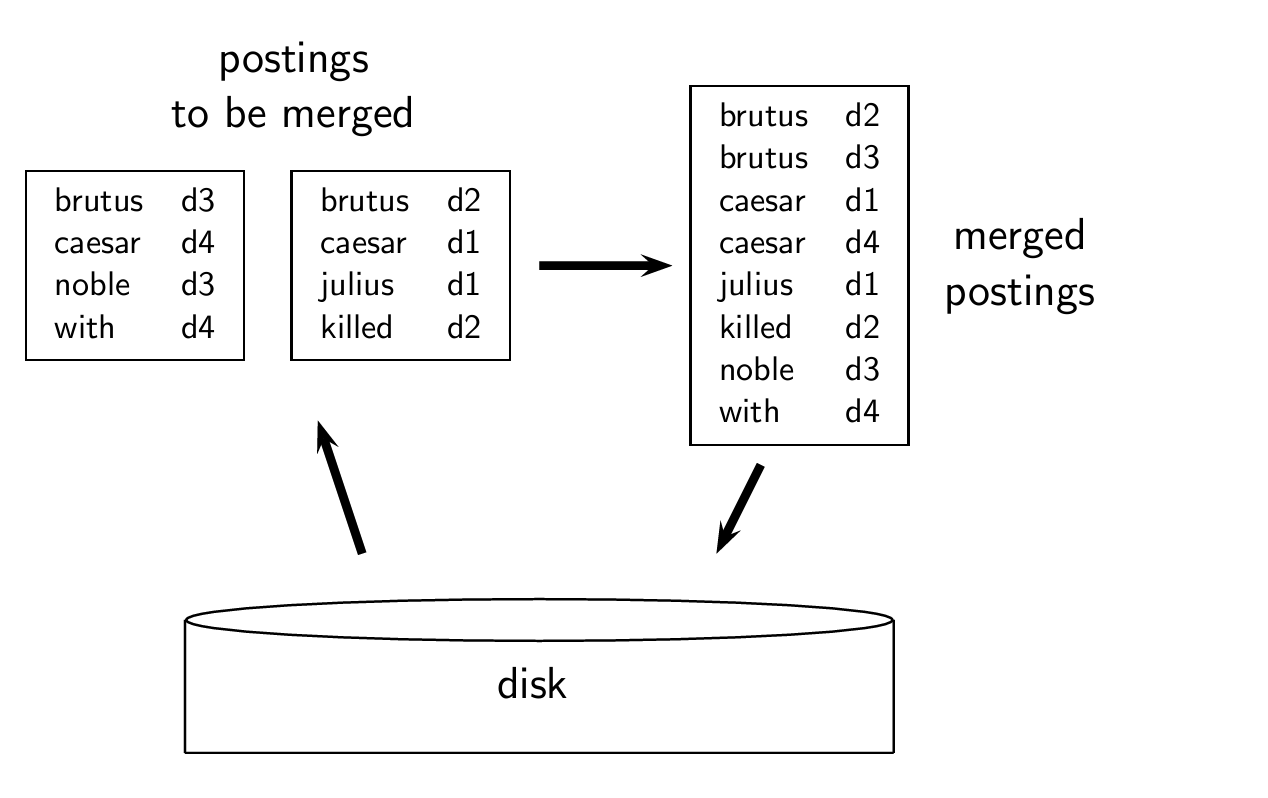
Single-pass in-memory indexing

이하 SPIMI.
블록 별로 독립적인 딕셔너리를 만들고, 정렬하지 않는다.

SPIMI-Invert

MapReduce for index construction

Dynamic indexing: Simplest approach

디스크에 메인 인덱스를 유지한다.
새 문서는 메모리의 작은 보조 인덱스로 이동한다.
메모리, 디스크의 인덱스를 모두 보면서 서치하고, 결과를 병합한다.
주기적으로 보조 인덱스를 big index에 병합한다.

Take-away today

5장에서 배울 내용은 아래와 같다.

  • IR 시스템에서 compression을 할 동기
  • inverted index의 딕셔너리 컴포넌트 압축하는 법
  • inverted index의 postings 컴포넌트 압축하는 법
  • Term 통계: 문서 컬렉션에서 용어 배포하는 법

2. Compression

Why compression? (in general)

IR 말고도 많은 분야에서 압축 기술을 쓴다.
일반적으로, 왜 압축을 하면 좋은 걸까?

  1. disk 용량 덜 씀 -> 돈을 아낀다.
  2. 더 많은 자료를 메모리에 보관 -> 속도 향상
  3. 디스크에서 메모리로 데이터 전송 속도 향상 -> 다시 속도 향상
  • 압축 데이터를 읽은 후 메모리 압축 해제를 하는 게, 압축 안 된 데이터 읽는 것보다 빠르다.
  1. 전제: 압축 해제 알고리즘은 빠르다.

Why compression in information retrieval?

그럼 IR에서는 왜 압축 기술을 쓰는 것일까?

  • 먼저, 딕셔너리를 위한 공간 고려

  • 딕셔너리 압축의 주요 동기: 메인 메모리에 보관할 수 있을 만큼 작게 만들기

  • postings file의 경우

  • 동기: 필요한 디스크 공간을 줄이고, 디스크에서 읽는 데 필요한 시간을 줄인다.
    ※ 대현 검색 엔진은 게시글의 상당 부분을 메모리에 보관한다.

딕셔너리와 postings에 대한 다양한 압축 방식을 고안할 것이다.

Lossy vs lossless compression

손실 압축 vs 무손실 압축

  1. 손실 압축: 일부 정보 버리기
  • 우리가 자주 사용하는 몇 가지 전처리 단계는 손실 압축이다.
  • downcasing, stop words, porter, 숫자 제거 등
  1. 무손실 압축: 모든 정보가 보존된다.
  • 인덱스 압축에서 주로 수행하는 작업

3. Term statistics

Model collection: The Reuters collection

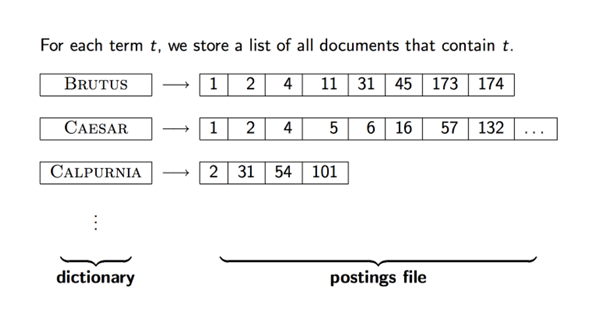
4장에서 이런 표를 본 적이 있었을 것이다.

Effect of preprocessing for Reuters

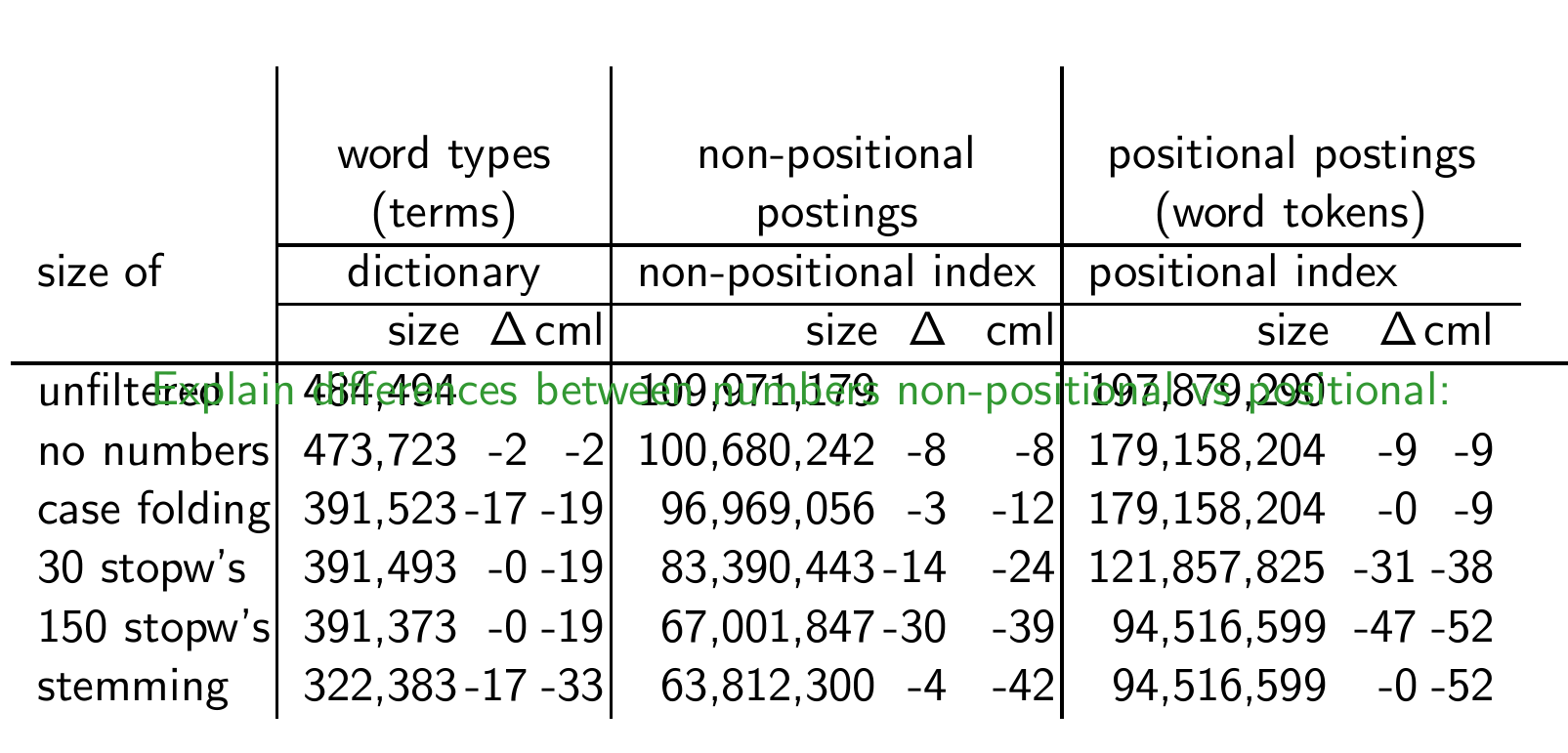
Reuter을 전처리하는 것의 효과는 어떤 게 있을까?
-> 크기가 엄청 줄어든다.

non-positional vs positional 차이?

How big is the term vocabulary?

즉, 얼마나 많은 words들이 term vocabulary에 있는가?
상한선이 있다고 가정해도 될까?
-> No. 길이가 20이면, 최소 7020 ≈ 1037개의 word가 있을 것이다.
그리고 이것은 컬렉션 크기에 따라 계속 늘어날 것이다.

Heaps’ law: M = kT^b

M=어휘의 크기, T=컬렉션에 있는 토큰 수

30 ≤ k ≤ 100, b ≈ 0.5

힙의 법칙은 로그-로그 공간에서 선형이다.

이는 로그-로그 공간에서 컬렉션 크기와 어휘 크기 사이의 가장 간단한 관계이다.

경험 법칙 (Empirical law)

Heaps' law for Reuters

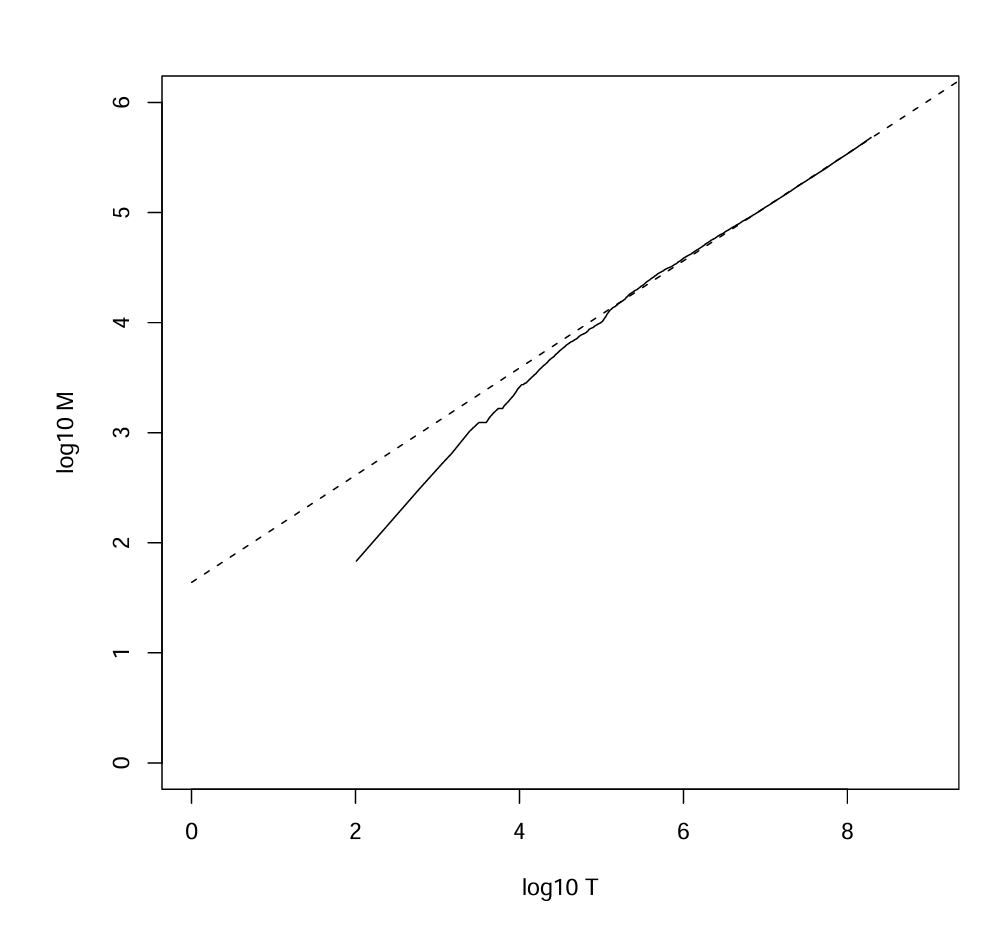
Heap's law는 문서 컬렉션 크기가 증가함에 따라 vocabulary의 크기가 어떻게 증가하는지를 모델링하는 경험적 법칙이다.
이 법칙에 따르면, 어휘집의 크기는 전체 토큰 수의 특정한 제곱근에 비례하여 증가한다.

Heap's law를 통해 큰 텍스트 데이터베이스에서 예상되는 어휘집의 크기를 추정할 수 있다.

Empirical fit for Reuters

Reuters 데이터에 대한 Heap's law의 적합성

Heap's law는 특정 크기의 컬렉션에 대한 vocabulary의 크기를 예측하는 데 사용된다.

Exercise

  1. 철자 오류를 포함시키는 것 vs 철자 오류를 자동으로 수정하는 것이 Heap's law에 미치는 영향
    -> 철자 오류를 포함시킬 경우 어휘 크기가 인위적으로 늘어날 것이기 때문에 자동으로 수정하는 것이 실제 언어 사용에 대한 더 근접한 측정치를 보일 것이다.

  2. 주어진 데이터를 바탕으로 M 계산하기
    -> K은 30, b는 0.5 나왔다.

Zipf's law

어휘의 증가를 특성화했다.

컬렉션에 얼마나 많은 frequent terms, infrequent terms가 포함되는지도 알고 싶다.

자연어에는 매우 빈번한 term이 조금 있고, 대부분은 매우 드물다.

Zipf의 법칙:

Zipf 법칙은 멱법칙(power law)의 한 예로 볼 수 있다.

멱법칙은 어떤 양이 다른 양의 거듭제곱에 비례하여 변하는 관계이다.

이미지에서 언급된 수식 cfi = c / i^k 에서는 이 관계를 나타내는 데 있어서 k는 -1이라고 명시되어 있습니다. 이는 Zipf의 법칙의 전형적인 형태로, 각 단어의 빈도(cfi)가 그 단어의 순위(i)의 역수에 비례한다는 것을 의미합니다.
수식 log(cfi) = log(c) + k * log(i)는 멱법칙 관계를 로그 스케일로 변환한 것입니다. 로그 변환을 사용하는 이유는 큰 범위에 걸쳐 분포하는 데이터를 보다 직선적으로 나타내고, 이로 인해 데이터의 경향을 보기 쉽게 만들기 위해서입니다.
이 경우 k가 -1일 때, 이 수식은 Zipf의 법칙을 로그-로그 플롯으로 표현할 수 있게 해줍니다. 이러한 플롯에서는 데이터가 직선에 가까울수록 멱법칙 관계를 잘 따르고 있다는 것을 나타냅니다.
따라서, cfi는 i에 따라 변하는 단어의 빈도를 나타내고, c는 상수로서 가장 빈번한 단어(1위 단어)의 빈도를 나타냅니다. 로그 변환을 취하면, 이 관계가 선형적인 형태로 표현될 수 있으며, 이는 데이터 분석이나 시각화에서 매우 유용합니다.

Zipf's law for Reuters

구체적인 수치까지 알 필요는 없다. 핵심 인사이트만 가져가자.
빈번한 용어는 적고 희귀한 용어는 많다.

4. Dictionary compression

Dictionary compression

딕셔너리는 postings file에 비하면 작다.
그런데 이걸 memory에 넣고 싶다.
또한, 다른 애플리케이션, 휴대폰, 온보드 컴퓨터, 빠른 시작도 고려해야 한다.

따라서 딕셔너리 압축은 중요하다.

Recall: Dictionary as array of fixed-width entries

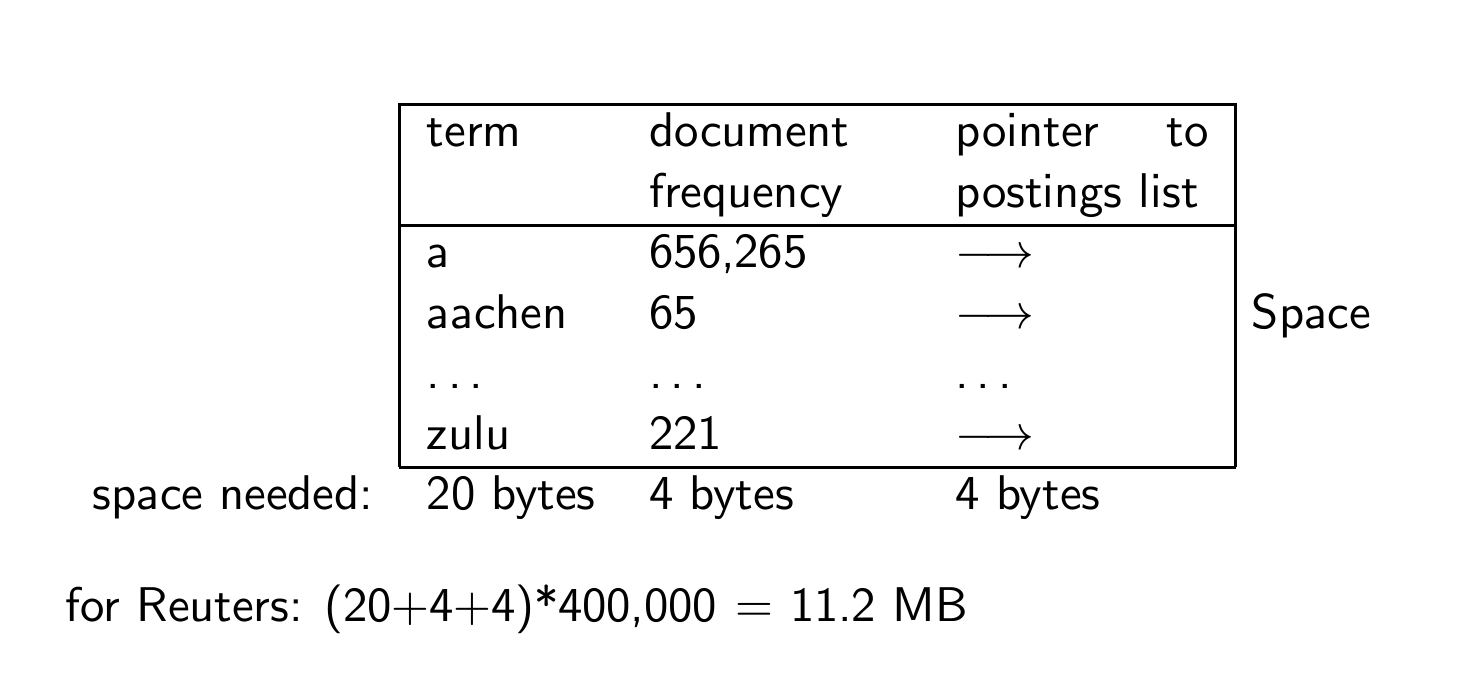
Reuters에서는 (20+4+4)*400000 gotj chd 11.2MB가 든다.
400000은 word type이다.

Fixed-width entries are bad.

term 열에 있는 대부분의 바이트가 낭비된다.
길이 1의 term에 20바이트를 할당한다.
우리는 hydrochlorofluorocarbons supercalifragilisticexpialidocious는 처리할 수도 없는데 말이다.
영어 용어의 평균 길이는 8자 정도이다.
한 term당 평균 8자를 어떻게 해야 쓸 수 있을까?

Dictionary as a string

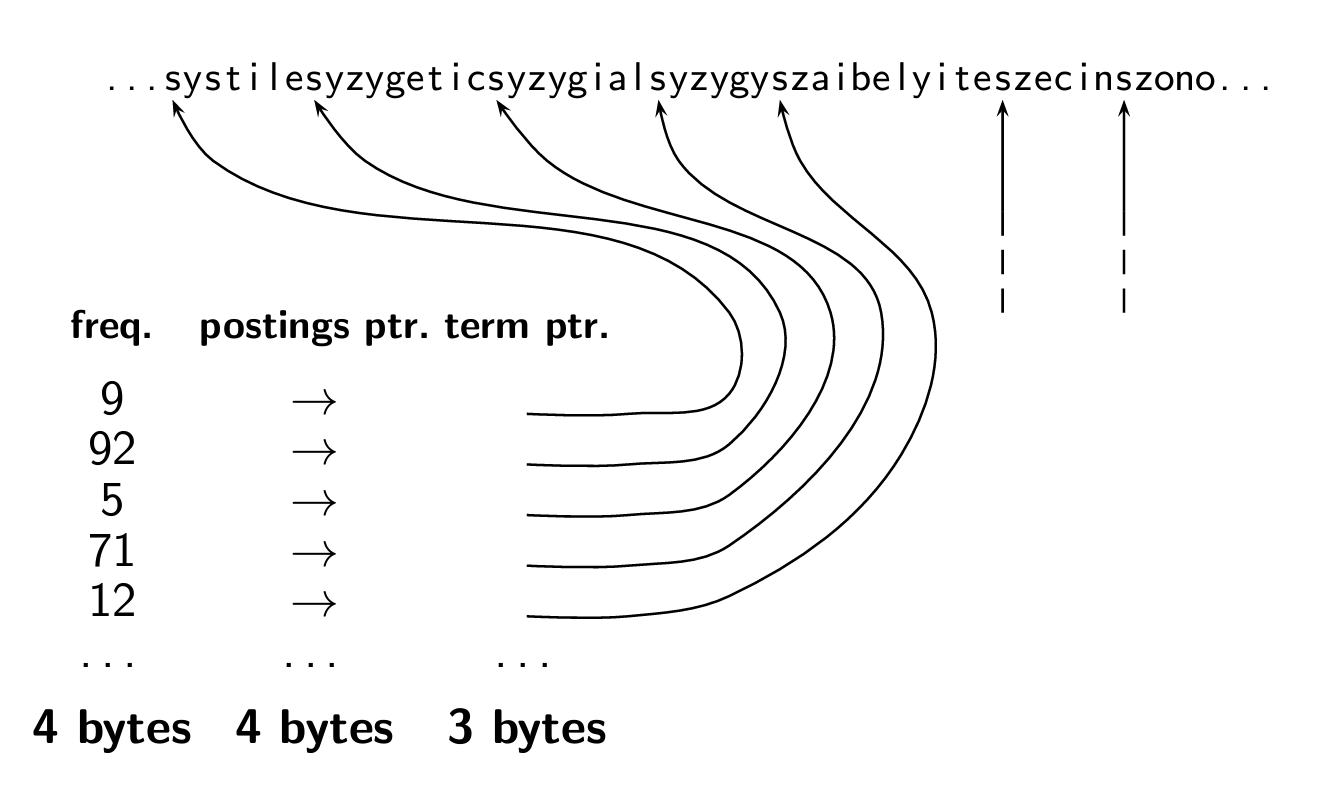
한 term당 20바이트씩 주는 게 아니라, 딕셔너리를 하나의 연속된 문자열로 표현한다.
각 단어는 문자열 내에서 고유의 위치를 가지며, 다른 필드와 함께 여러 바이트를 할당하여 각 단어에 대한 추가 정보를 제공한다.

  • Frequency: 단어가 콜렉션에서 발생하는 빈도 (4바이트)
  • Postings Pointer: 해당 단어가 등장하는 문서들의 목록 또는 위치를 가리키는 포인터 (4바이트)
  • Term Pointer: 단어가 문자열 내에서 시작하는 위치 가리키는 포인터 (3바이트)

Space for dictionary as a string

위처럼 만들면 저장 공간은 아래처럼 할당된다.

  • 4바이트: 각 단어의 빈도
  • 4바이트: 각 단어의 postings list 가리키는 포인터
  • 평균 8바이트: 실제 단어 저장
  • 3바이트: 딕셔너리 내의 위치 가리키는 포인터

log2(8400000)은 24비트 미만이므로, 3바이트로 8400000 위치를 해결할 수 있다.

결과적으로, 400,000개의 단어를 가진 딕셔너리는 대략 400,000*(4+4+3+8)=7.6MB 공간을 차지한다.

고정 너비 배열은 11.2MB였으므로 더 효율적으로 공간을 사용할 수 있게 됐다.

Dictionary as a string with blocking

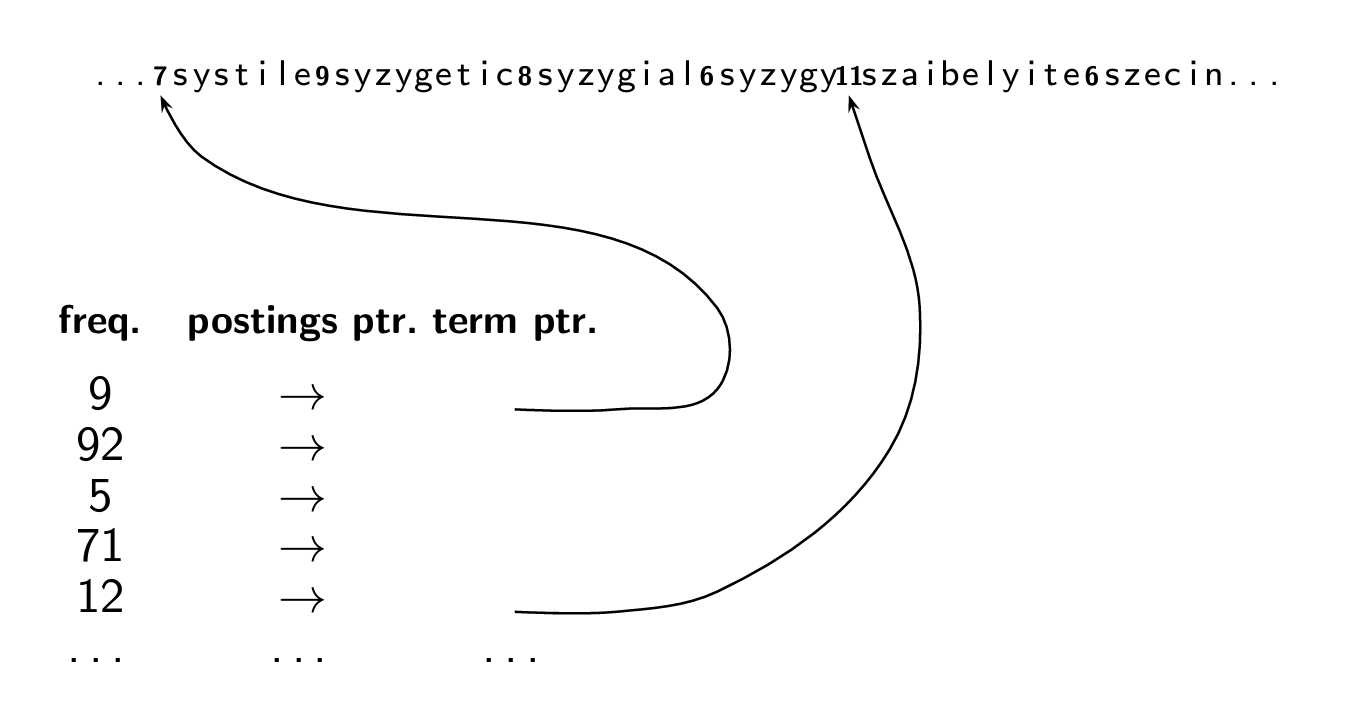
이번엔 blocking 기법을 사용하여 딕셔너리를 저장해보자.

blocking은 저장 공간을 절약하기 위해 사용하는데, 특정 수의 연속된 단어들(블록)을 그룹화하고 이들 간에만 포인터를 사용한다.

그림에서 "7systile9syzgyet..."에서 '7'은 'systile'이라는 단어가 7개의 문자를 가지고 있음을 나타낸다.

이 방법을 사용하면 각 단어의 시작점을 특정할 수 있으므로 모든 단어에 대한 개별 포인터를 저장할 필요가 없다.

  • Frequency: 단어의 빈도수
  • Postings Pointer: 문서 목록에 대한 포인터
  • Term Pointer: 블록 내 첫 번째 단어의 시작점을 가리키는 포인터

Space for dictionary as a string with blocking

아까보다 더 공간을 절약할 수 있다.

예시로, 블록 크기가 k=4라고 가정하자.
이전에는 포인터를 사용하기 위해, 각 단어에 3바이트씩 총 4*3바이트가 필요했다.
그러나 blocking을 사용하면 3바이트의 한 포인터만 필요하고, 각 단어의 길이를 나타내는데 추가로 4바이트가 필요하다.
즉, 블록 당 총 12바이트가 필요했으나 이제는 7바이트만 필요하므로 블록 당 5바이트를 절약할 수 있게 됐다.

각 블록 당 5바이트를 절약하므로, 5*(400000/4)해서 총 0.5MB를 절약한다.

결과적으로, 딕셔너리의 크기가 7.6MB에서 7.1MB로 줄어든다.

Lookup of a term without blocking

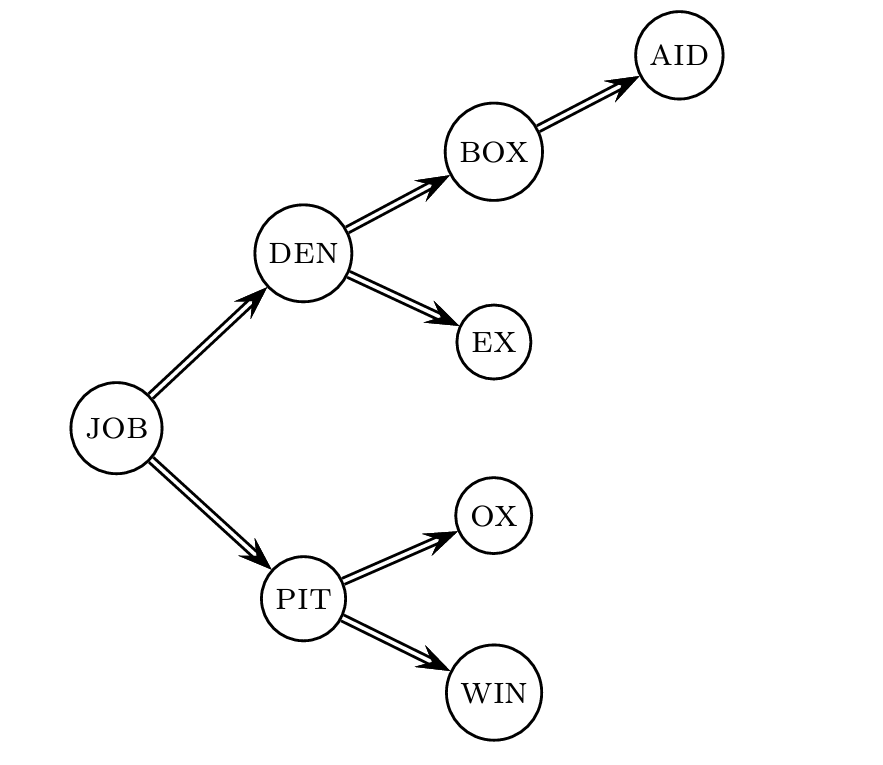
Lookup of a term with blocking: (slightly) slower

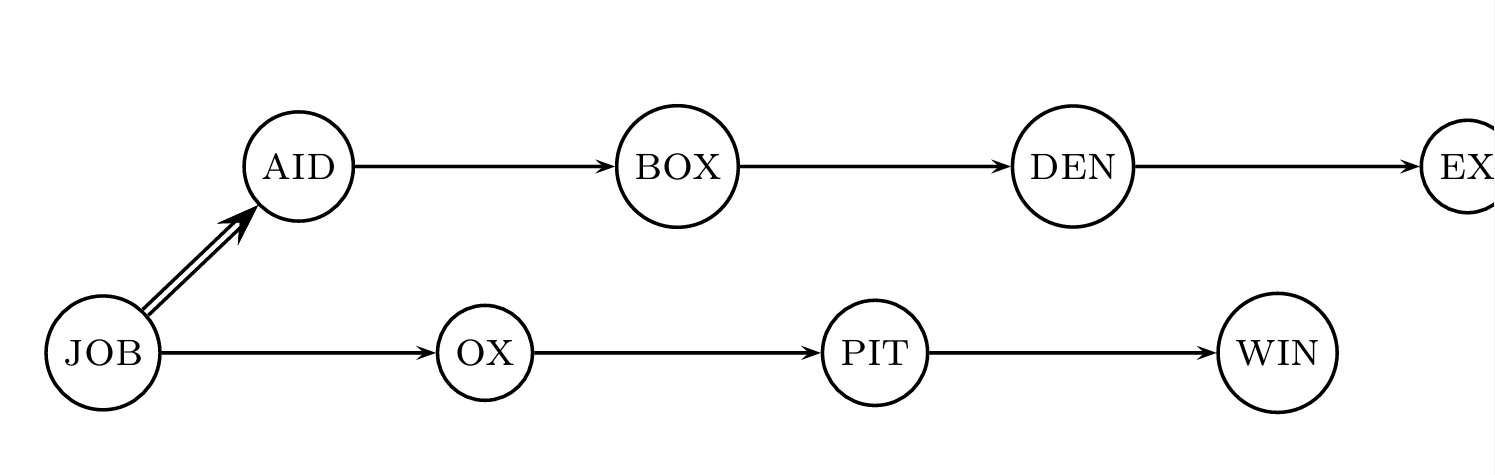
연속된 용어들을 블록으로 그룹화하고, 각 그룹의 시작 term만이 다음 블록의 시작 term을 가리키는 포인터를 가진다.
첫 번째 블록의 시작 용어부터 시작하여, 원하는 용어가 포함된 블록을 찾을 때까지 각 블록의 시작 용어들을 순차적으로 방문한다.

Front coding

Front Coding은 문자열 데이터를 압축하는 데 사용되는 기술 중 하나이다.
일련의 문자열들이 공유하는 공통된 prefix를 활용한다.

Dictionary compression for Reuters: Summary

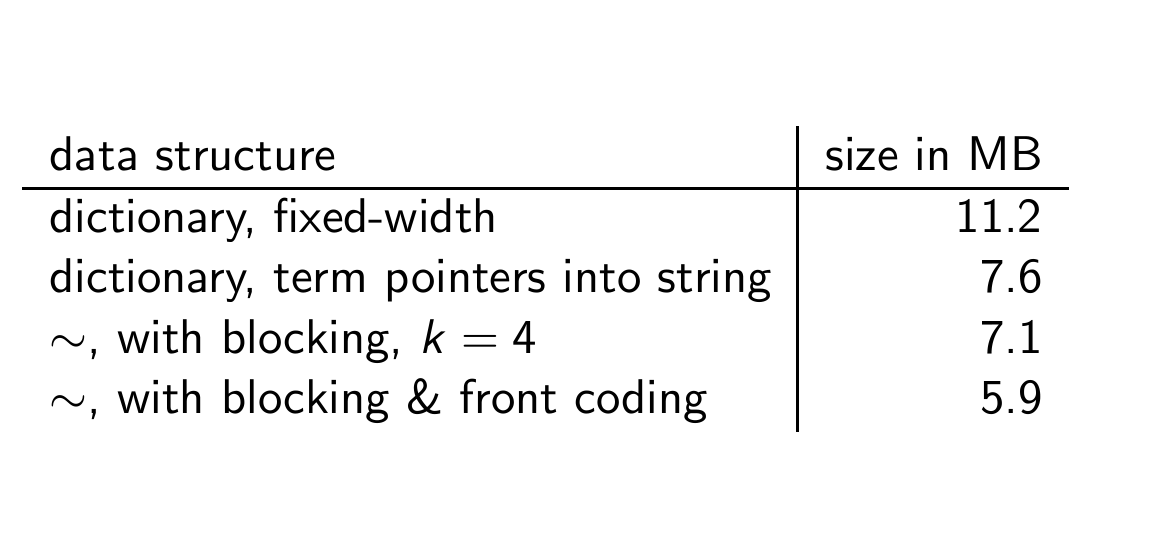
블록에 프론트 코딩 기법까지 쓰면 용량이 정말 많이 줄어든다.

Exercise

front coding에서 어떤 prefix들이 사용되어야 하는가? 그리고 그것의 tradeoff는 무엇인가?
=> 압축률과 검색 속도. 더 긴 공통 접두사를 사용하면 압축률이 높아질 수 있지만, 검색할 때마다 더 많은 문자를 비교해야 하므로 검색 속도가 느려질 수 있다.
더 많은 공간을 절약하고자 할 때는 더 많은 단어를 포함하는 접두사를 선택할 수 있지만, 이는 데이터를 처리하고 업데이트하는 데 더 많은 시간이 걸릴 수 있다.

  • Input: term 리스트 (= term vocabulary)
  • Output: front coding에서 사용될 prefix 목록

5. Postings compression

Postings compression

postings는 딕셔너리보다 10배 이상 더 크다.

핵심 사항은, 각 게시글을 간결하게 저장하는 것이다.

우리가 사용하는 posting은 docID다.

Reuters(800,000개의 문서)의 경우, 4바이트 정수를 사용할 때 docID당 32비트를 사용한다.
또는 log2 800,000 ≈ 19.6 < 20비트를 docID당 사용할 수 있다.
우리의 목표는 docID당 20비트보다 훨씬 적은 비트를 사용하는 것이다.

Key idea: Store gaps instead of docIDs

전체 docID를 저장하는 대신, 연속적인 docID 간의 gap을 저장한다.

예를 들어 'COMPUTER'라는 단어에 대한 postings list에는 283154, 283159, 283202와 같은 docID가 포함되어 있다.
Gap을 저장하면, 첫 번째 docID 283154를 전체로 저장한 다음, 그 다음 docID까지의 gap인 5와 43을 저장한다.

Gap 인코딩의 장점

  • 간격 크기: 자주 등장하는 용어의 경우 간격이 작다.
    즉, 인기 있는 단어가 있는 문서는 종종 가까이 있어서 작은 숫자로 간격을 나타낼 수 있다.
  • 비트 인코딩: 작은 간격은 적은 비트로 인코딩할 수 있다. 예를 들어, 20비트보다 적은 비트를 사용하여 효율적으로 간격을 인코딩할 수 있다.

Gap encoding

The 처럼 자주 쓰이는 단어는 작은 숫자로 간격을 나타낼 수 있다.

Variable length encoding

목표

  • 드문 용어는 20비트를 사용한다.
  • 매우 자주 등장하는 용어는 몇 개의 비트만 사용한다.

위 목표를 실행하기 위해서는, 각 gap의 크기에 따라 비트 수가 달라지는 인코딩 방식을 고안해야 한다.

Variable byte (VB) code

VB 코드: 압축 기법

많은 상업 및 연구 시스템에서 사용되며, 가변 길이 인코딩과 메모리 정렬 사이의 좋은 저기술(low-tech) 조합이다.

각 바이트의 상위 비트(맨 왼쪽)는 continuation bit로 지정되며, 이 비트는 추가 바이트가 뒤따라오는지 여부를 나타낸다.

인코딩 방법

  • 단일 바이트로 충분한 경우: gap 값이 7비트 이내에 들어맞으면, 해당 숫자를 7비트로 이진 인코딩하고 continuation bit를 1로 설정하여 이것이 마지막 비트임을 나타낸다.
  • 여러 바이트가 필요한 경우: 낮은 순서의 7비트를 먼저 인코딩하고, continuation bit를 0으로 설정한 다음,더 높은 순서의 비트를 인코딩하기 위해 하나 이상의 추가 바이트를 사용한다.
    각 추가 바이트도 동일한 방법을 사용하여 인코딩되며, 마지막 바이트만 continuation bit가 1이 된다.

VB code examples

예시를 보자.
5는 gap이 7비트 내로 들어맞은 경우기 때문에 그냥 저렇게 쓰면 된다.

214577같은 경우 7비트를 넘기 때문에, 위에서 얘기한 인코딩 방법을 따라야 한다.

  1. 214577을 2진수로 변환한다.
  2. 7비트씩 끊는다.
  3. 마지막 바이트에는 1을 붙인다.

VB code encoding algorithm

바이트를 계산한다.

VB code decoding algorithm

디코딩한다.

Other variable codes

바이트 대신 다른 정렬 단위를 사용할 수 도 있다.
32비트(words), 16비트, 4비트(nibbles) 등

가변 바이트 정렬은 작은 간격이 많은 경우 공간을 낭비하게 되므로 니블이 더 효과적이다.

다양한 수의 공백을 하나의 연구에 효율적으로 패킹하는 단어 정렬 코드에 대한 연구가 있다.

Gamma codes for gap encoding

bitlevel code로 내려가서 더 압축할 수도 있다.
가장 대표적인 예시가 Gamma code이다.
gamma 코드를 도입하기 위해선 unary code가 필요하다.

🔔 Unary Code?
그냥 숫자 크기만큼 1 적고 마지막에 0달면 끝이다.

Gamma code

Gamma 코드는 간격 또는 숫자를 인코딩하는 비손실 압축 기법이다.

Gamma 코드는 숫자를 두 부분으로 나눈다.

  • length: 오프셋의 길이. 101의 경우 -> 3
  • offset: 숫자를 이진 형태로 표현했을 때, 선행 을 제외한 나머지 부분.
    ex) 1101의 오프셋은 101
  • 길이와 오프셋을 연결하여 인코딩한다.
    -> 1110 + 101 => 1110101

Gamma code examples

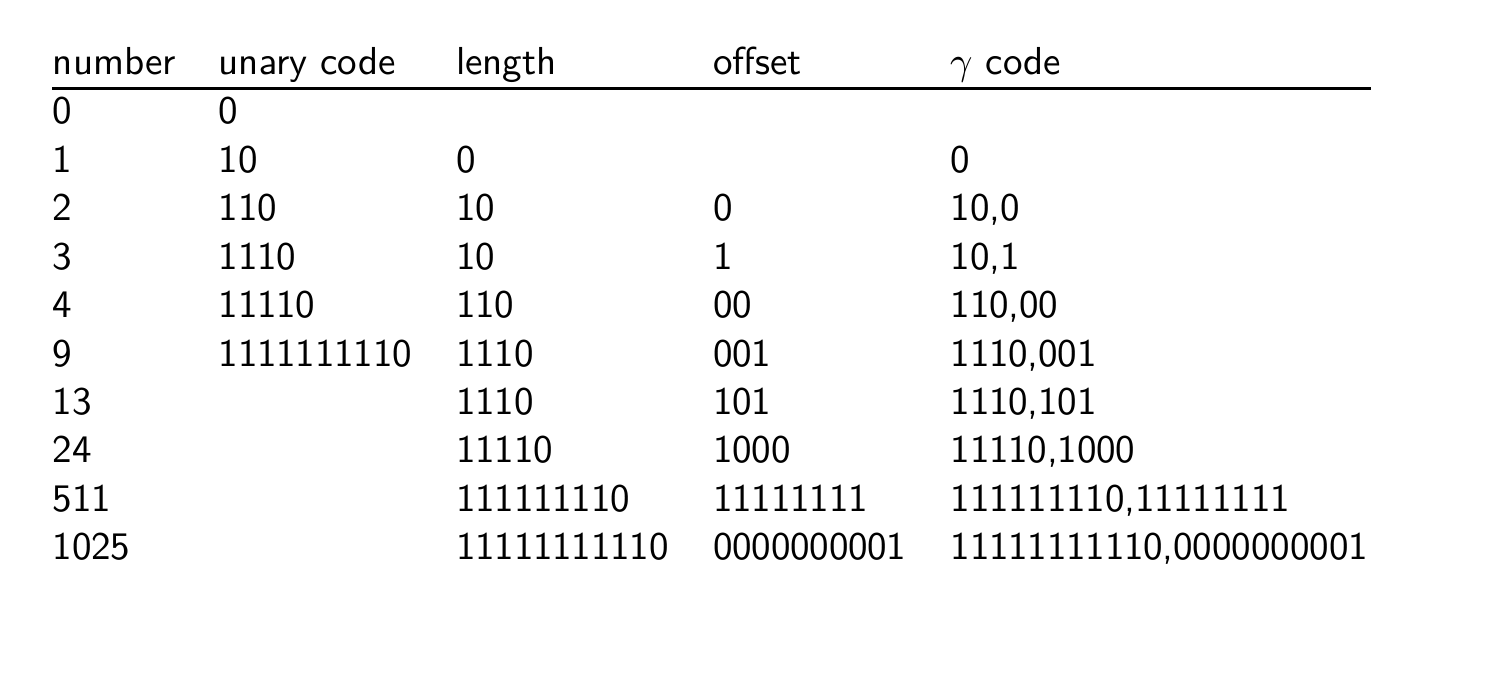
Exercise

130에 대해

  • variable byte code 계산
  • gamma code 계산

Length of gamma code

offset 길이는 log2 G 비트이다.
length 길이는 log2 G + 1 비트이다.

그래서 전체 코드의 길이는 2 * log2 G + 1 비트이다.

-> 감마 코드의 길이는 항상 홀수이다.

감마 코드는 최적의 인코딩 길이 log2G의 2승 이내이다.
(gap G의 빈도가 log2 G에 비례한다고 가정하면 대략 참이다.)

Gamma code: Properties

  • prefix-free(접두사 자유): Gamma 코드는 유효한 코드 단어가 다른 어떤 유효한 코드의 접두사가 아니게 된다.

  • 최적화: 인코딩은 3배 이내에서 최적화되며, 추가적인 가정하에 2배 이내에서 최적화될 수 있다.

  • 보편적 사용 가능: 어떤 분포의 간격에서도 사용 가능하다.

  • parameter-free(파라미터-자유): 인코딩해야 할 데이터에 따라 조정할 파라미터가 없다.

Gamma codes: Alignment

Gamma 코드는 정렬 문제에서도 효율적이다.

  1. 단어 경계: 컴퓨터는 8/16/32비트 등의 단어 경계를 가지고 있는데, 이런 단위로 데이터를 가장 효과적으로 처리한다.
  2. 비트 단위의 압축과 조작: 비트 단위로 데이터를 압축하고 조작하는 것은 시스템에 따라 느릴 수 있다.
  3. 가변 바이트 인코딩: 가변 바이트 인코딩은 이러한 단어 경계에 맞춰 정렬되기 때문에 더 효율적일 수 있다.
  4. 간단함: 가변 바이트 인코딩은 개념적으로 더 단순하고 추가적인 공간 비용이 거의 들지 않음에도 불구하고 효유렂ㄱ이다.

Gamma 코드는 작은 숫자에 대해 매우 공간 효율적이다.
가변 바이트 코드는 인코딩과 디코딩 속도에서 이점을 가질 수 있다.

Compression of Reuters

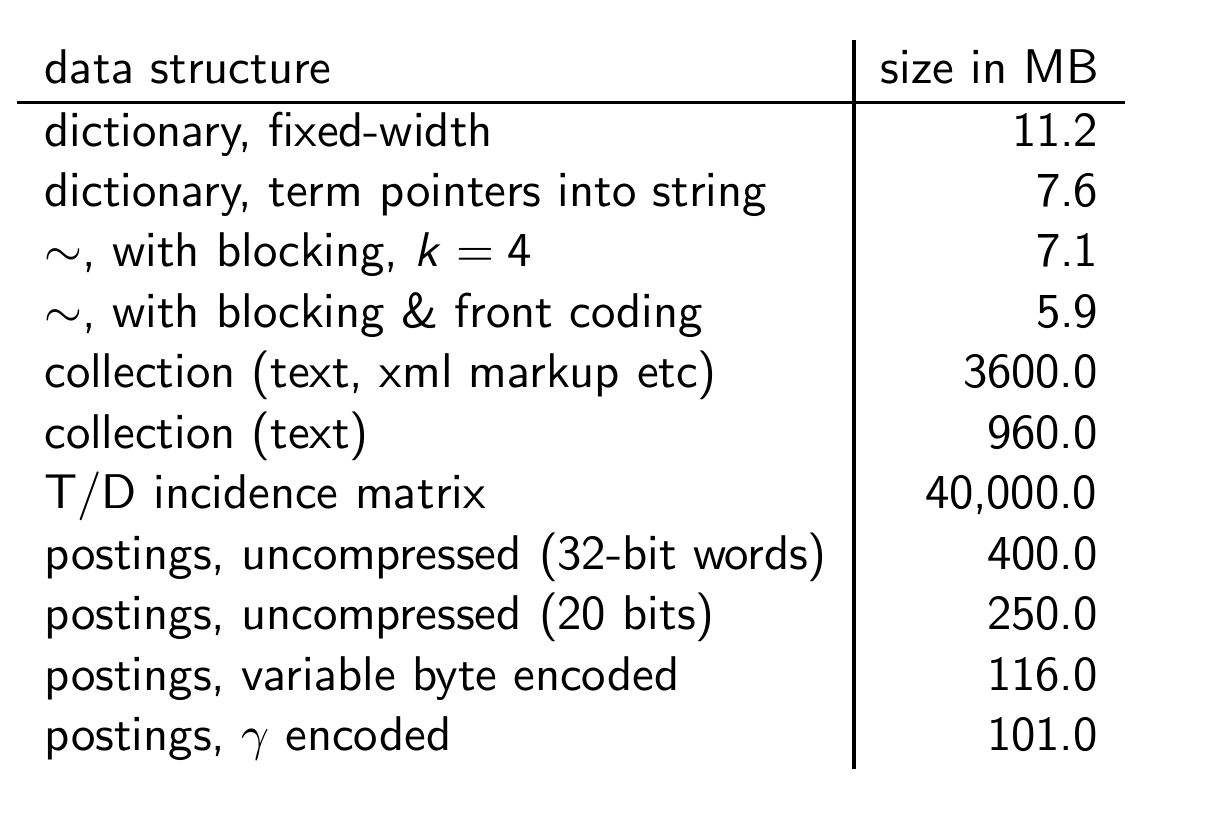
variable byte, 감마코드를 쓰니까 정말 많이 압축되었음을 확인할 수 있다.

Term-document incidence matrix

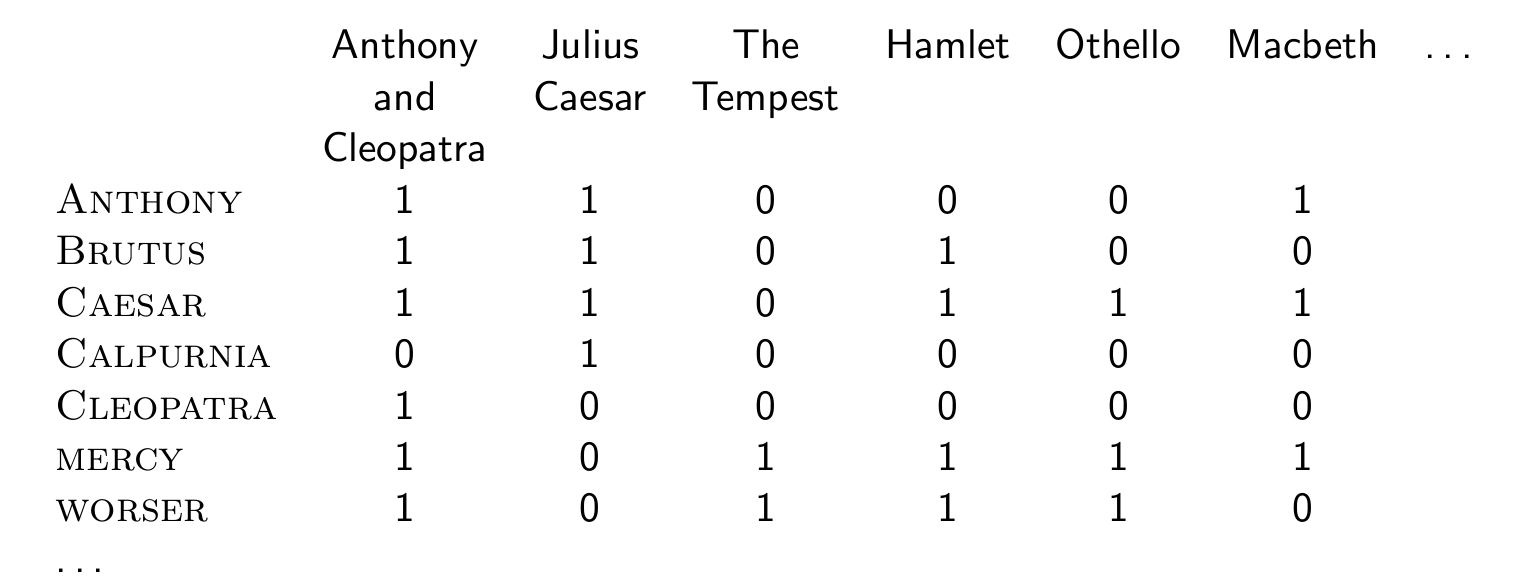
1장에서 했었다.

Summary

이제 공간 효율성이 매우 높은, boolean retrieval을 위한 인덱스를ㄹ 만들 수 있다.
컬렉션에 있는 전체 텍스트 크기의 10~15%에 불과하다.

하지만 위치 및 빈도 정보를 무시했기 때문에, 실제로는 공간 절약 효과가 계산한 것보다는 적다.

※ 추가로 공부할 점

  • Heap 법칙
  • Zipf 법칙
  • 딕셔너리 압축 계산
  • Postings 압축 계산
  • 가변 압축
profile
hoho
이전 포스트

[Information Retrieval] 4. Index Construction

0개의 댓글