http://cislmu.org 와 학교 수업을 토대로 정리합니다.
1. Recap
Dictionary as array of fixed-width entries

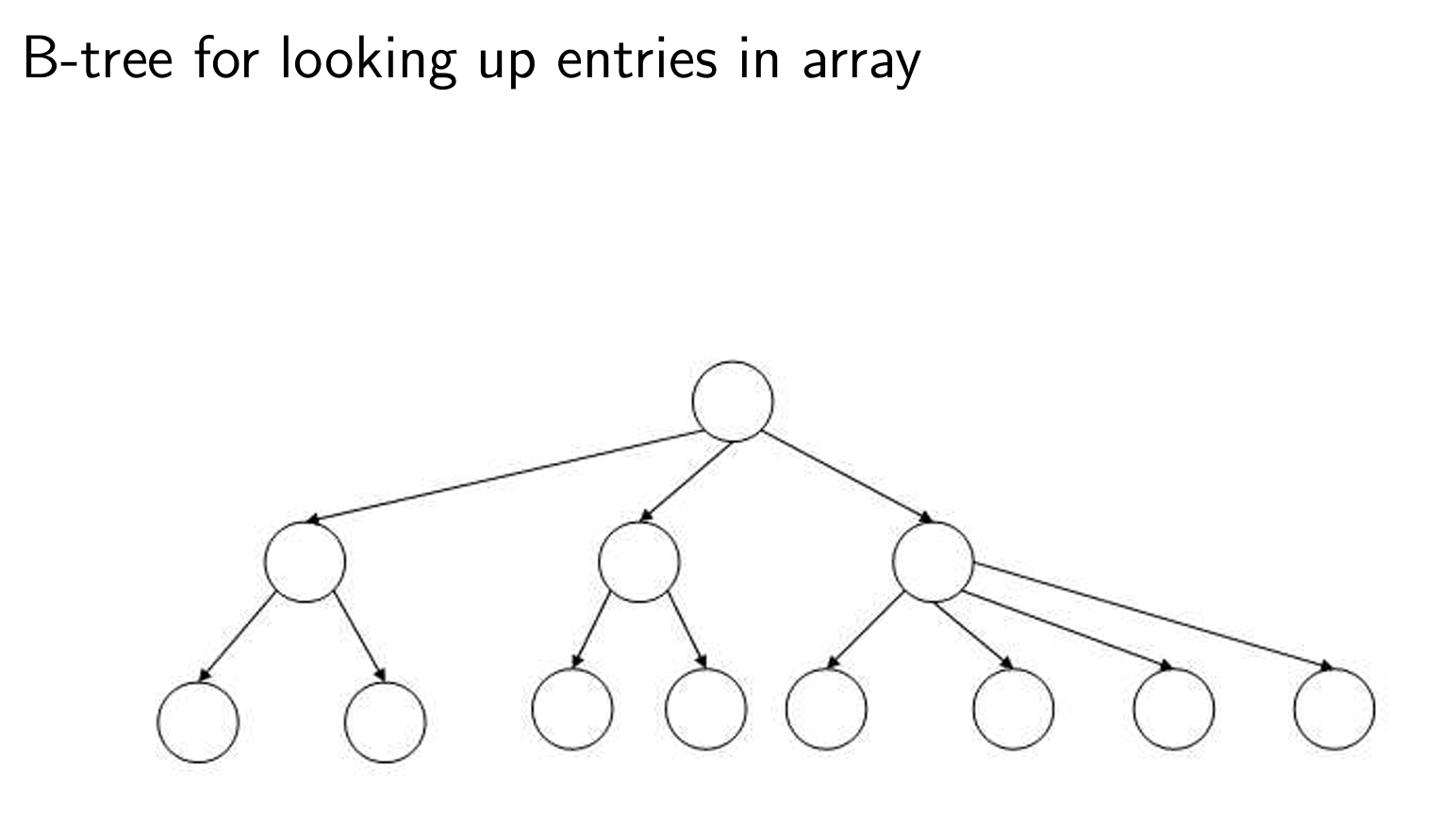
B-tree for looking up entries in array
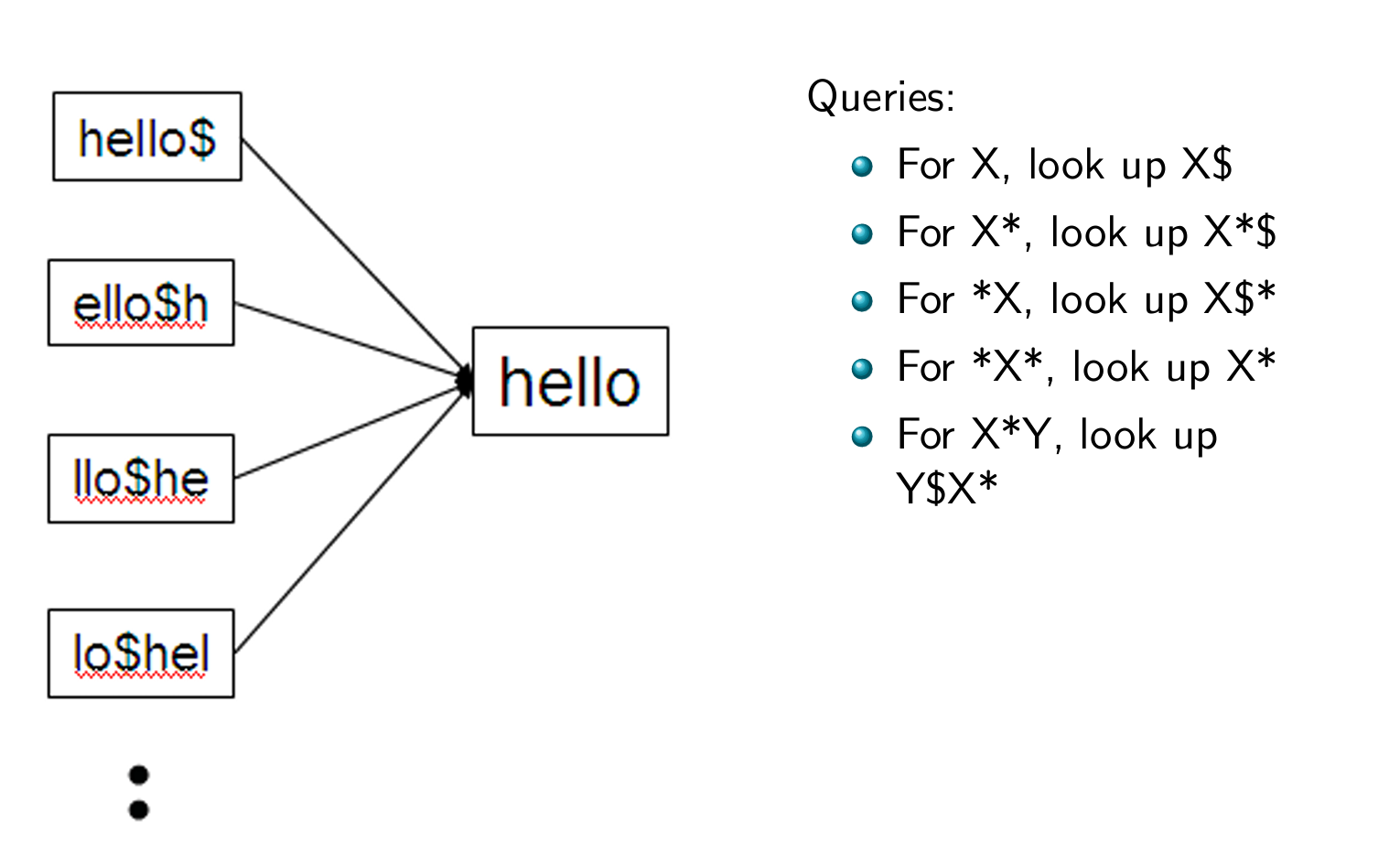
Wildcard queries using a permuterm index
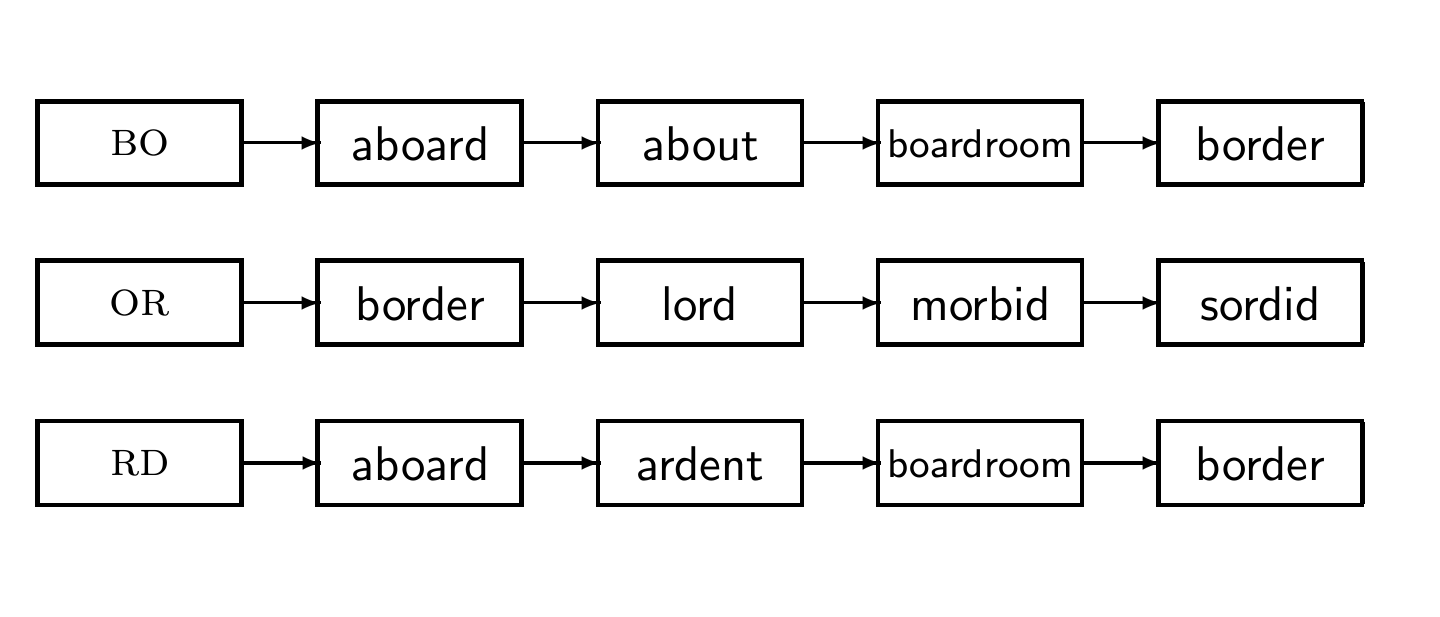
k-gram indexes for spelling correction: bordroom
Levenshtein distance for spelling correction

Exercise: Understand Peter Norvig's spelling corrector

Take-away
4장에서 배울 핵심 개념은 아래와 같다.
- 두 index construction 알고리즘들: BSBI (간단함), SPIMI (현실적임)
- Distributed index construction: MapReduce
- Dynamic index construction: 컬렉션이 변경될 때 인덱스를 최신 상태로 유지하는 방법
2. Introduction
Hardware basics
정보 검색의 많은 설계 과정은 HW 제약 조건에 따라 이루어진다.
정보 검색을 설계하면서 제일 먼저, 필요한 하드웨어 기본 사항을 검토해야 한다.
- 메모리에서의 데이터 액세스 속도가 디스크보다 약 10배 정도 빠르다.
- 디스크 탐색은 idle 시간을 가진다. 디스크 헤드가 위치를 잡는 동안에는 데이터 전송이 이루어지지 않는다.
- 디스크에서 메모리로의 전송 시간을 최적화하기 위해서는, 작은 chunk들보다 하나의 큰 chunk를 전송하는 것이 더 빠르다.
- 디스크 I/O는 블록 단위(block-based)로 이루어진다. 전체 블록을 읽고 쓰는 것이 더 작은 chunk를 다루는 것보다 효율적이다. 블록 크기는 일반적으로 8KB~256KB 사이이다.
- IR 시스템에서 사용되는 서버들은 일반적으로 수 GB의 메인 메모리와 수 TB의 디스크 공간을 가지고 있다.
- 장애 허용(fault tolerance)은 비용이 많이 든다. 여러 대의 일반 장비를 사용하는 것이 하나의 장애 허용 장비를 사용하는 것보다 더 경제적이다.
🔔 왜 하나의 큰 chunk를 전송하는 게 여러 개의 작은 chunk를 전송하는 것보다 빠를까?
=> 작은 chunk들을 여러 번 읽을 때마다 디스크 헤드를 이동시켜야 하므로 seek time이 반복적으로 발생하는데, 하나의 큰 chunk를 읽을 때는 seek time이 한 번만 발생한다.
Some stats (ca. 2008)

정보 검색 시스템에서 사용되는 HW의 주요 특성들에 대한 일반적인 값들
RCV1 collection
RCV1: 정보 검색 및 텍스트 분류 연구에 사용되는 벤치마크 데이터셋
확장 가능한 index 구축 알고리즘을 적용하는 예시로서 Reuters RCV1 컬렉션을 사용할 것이다.
RCV1은 1995~1996년 Reuters에서 배포한 영어 뉴스 기사들을 수집한 것이다.
A Reuters RCV1 document

이런 영어 뉴스 기사들을 모아둔 것이다.
Reuters RCV1 statistics

term의 평균 빈도는? 4.5
term 당 바이트 수는 7.5인데, 왜 word type 당 바이트 수는 4.5인가? => 각 용어가 여러 문서에서 반복적으로 등장하기 떄문
positional posting은 몇 개인가? =>
Claude가 계산해주었다.
전체 non-positional posting의 수 (T) = 1억 개 (100,000,000)
문서의 수 (N) = 800,000
문서 당 평균 토큰 수 (L) = 200
positional posting의 수는 각 문서 내에서 용어의 위치 정보까지 포함하므로, 대략 문서 당 평균 토큰 수에 비례할 것입니다.
positional posting의 수 = non-positional posting의 수 (T) × 문서 당 평균 토큰 수 (L)
= 100,000,000 × 200
= 20,000,000,000 (200억 개)
따라서, positional posting의 수는 대략 200억 개 정도로 예상할 수 있습니다. 이는 non-positional posting에 비해 용어 위치 정보를 추가로 저장해야 하므로 인덱스의 크기가 상당히 커짐을 의미합니다.
🔔 Non-positional posting vs Positional posting
전자는 특정 term을 포함한 문서의 ID만을 반환한다.
후자는 ID와 함께 문서 내에서의 위치 정보까지 저장한다.
Exercise
저 알고리즘이 매우 큰 컬렉션으로 확장되지 않는 이유는 무엇인가?
3가지 정도의 이유가 있다.
-
인덱스 크기의 급격한 증가
: 문서 수가 증가함에 따라 inverted index의 크기도 빠르게 증가한다.
특히 positional posting을 사용할 경우, 인덱스 크기는 non-positional posting에 비해 문서 당 평균 토큰 수에 비례하여 증가한다. -
질의 처리 시간 증가: 인덱스 크기가 커짐에 따라 질의 처리 시간도 증가한다.
-
인덱스 구축 시간 증가: 문서 수가 많아질수록 인덱스를 구축하는 데 걸리는 시간도 증가한다.
3. BSBI algorithm
Goal: construct the inverted index
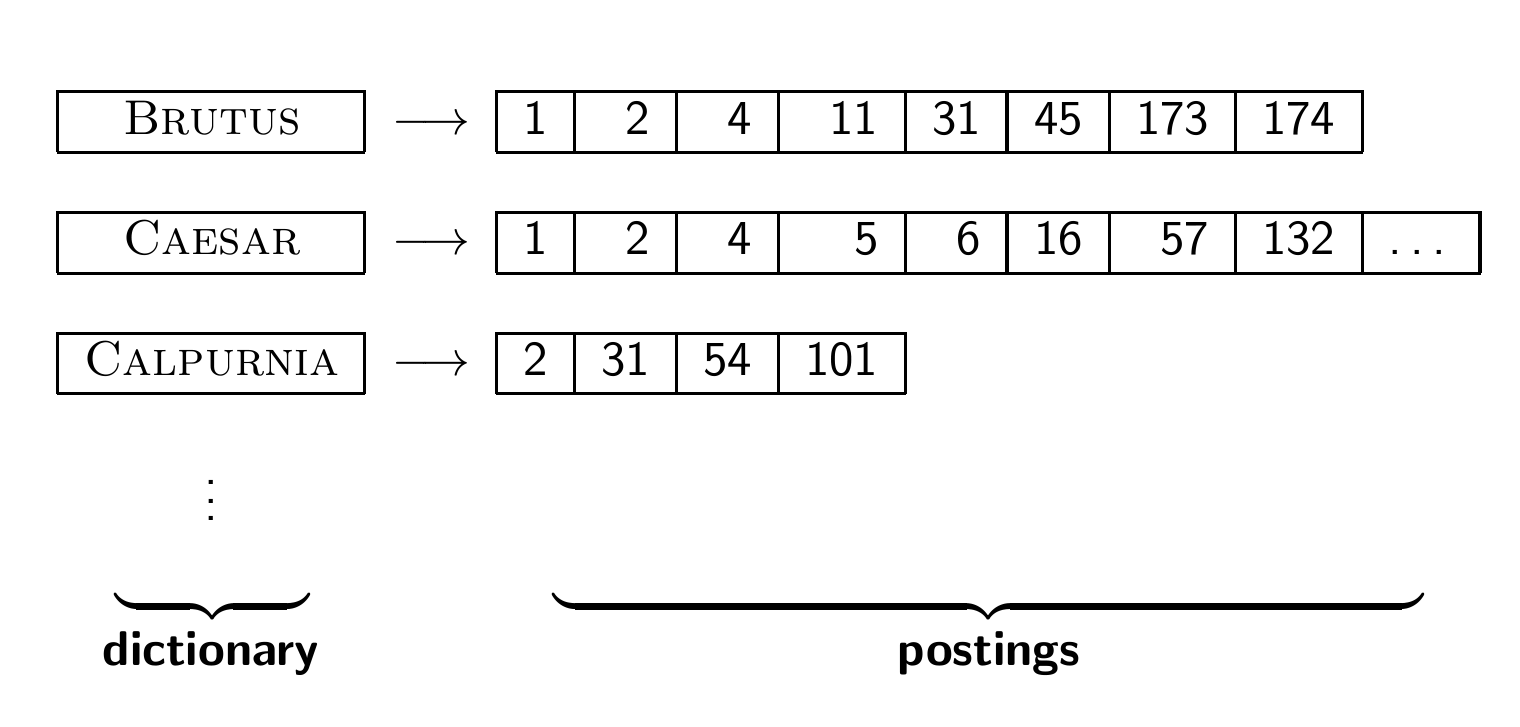
1장에서부터 계속 봤던 inverted index이다.
BSBI 알고리즘을 공부하여 inverted index를 구축하는 것이 목표이다.
Index construction in IIR1: Sort postings in memory
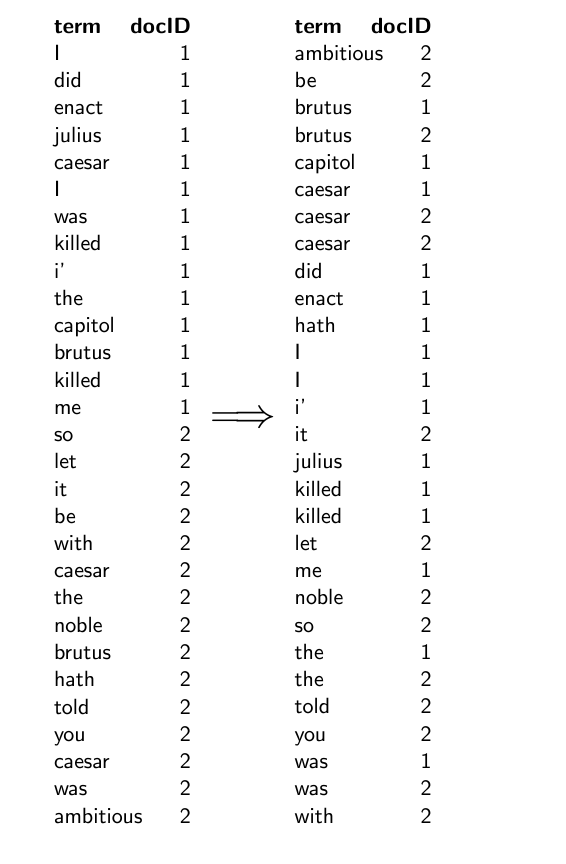
리스트를 만들면 그만인 게 아니라, 정렬을 무조건 해야 한다.
Sort-based index construction
index를 만들 때, 문서를 한 번에 하나씩 파싱한다.
그리고 어떤 term에 대한 최종 postings는 전체 문서 세트를 처리하기 전까지는 완전하지 못하다. (어떤 용어에 대한 모든 출현 정보를 알 수 없기 때문)
모든 게시물을 메모리에 보관한 다음 마지막에 메모리 내에서 정렬할 수 있을까?
-> 대규모 컬렉션이면 당연히 불가능하다.
그래서 중간 결과를 디스크에 저장해야 한다.
Same algorithm for disk?
메모리 대신 디스크를 쓰면, 위같은 index construction 알고리즘을 똑같이 사용할 수 있을까?
이것도 안된다. 왜냐하면 매우 큰 레코드 세트를 디스크에서 정렬하는 건 너무 느리기 때문이다. (디스크 검색 횟수가 너무 많다.)
따라서 외부 정렬 알고리즘이 필요하다.
"External" sorting algorithm (using few disk seeks)
외부 정렬 알고리즘은 대량의 데이터를 정렬할 때 사용되며, 메모리에 한 번에 로드할 수 없을 만큼 큰 데이터를 정렬해야 할 때 쓰인다.
예를 들어, T = 100,000,000 개의 non-positional postings를 정렬해야 한다고 하자. 각각의 posting은 12 bytes의 크기를 가진다. (termID 4 + docID 4 + term frequency 4)
그리고 저 1억 개를 나누어 담을 block을 정의해야 한다.
각각의 block은 10,000,000 개의 posting으로 구성된다.
이는 메모리에 쉽게 로드할 수 있는 양이고, RCV1에 대해 총 10개의 블록이 있다고 한다.
알고리즘의 기본 아이디어는 아래와 같다.
각 블록에 대해 아래 단계를 수행한다.
1. postings를 메모리에 축적한다.
2. 메모리에서 postings를 정렬한다.
3. 정렬된 block을 디스크에 쓴다.
그 후 이 블록들을 하나의 긴 정렬된 순서로 병합한다.
Merging two blocks
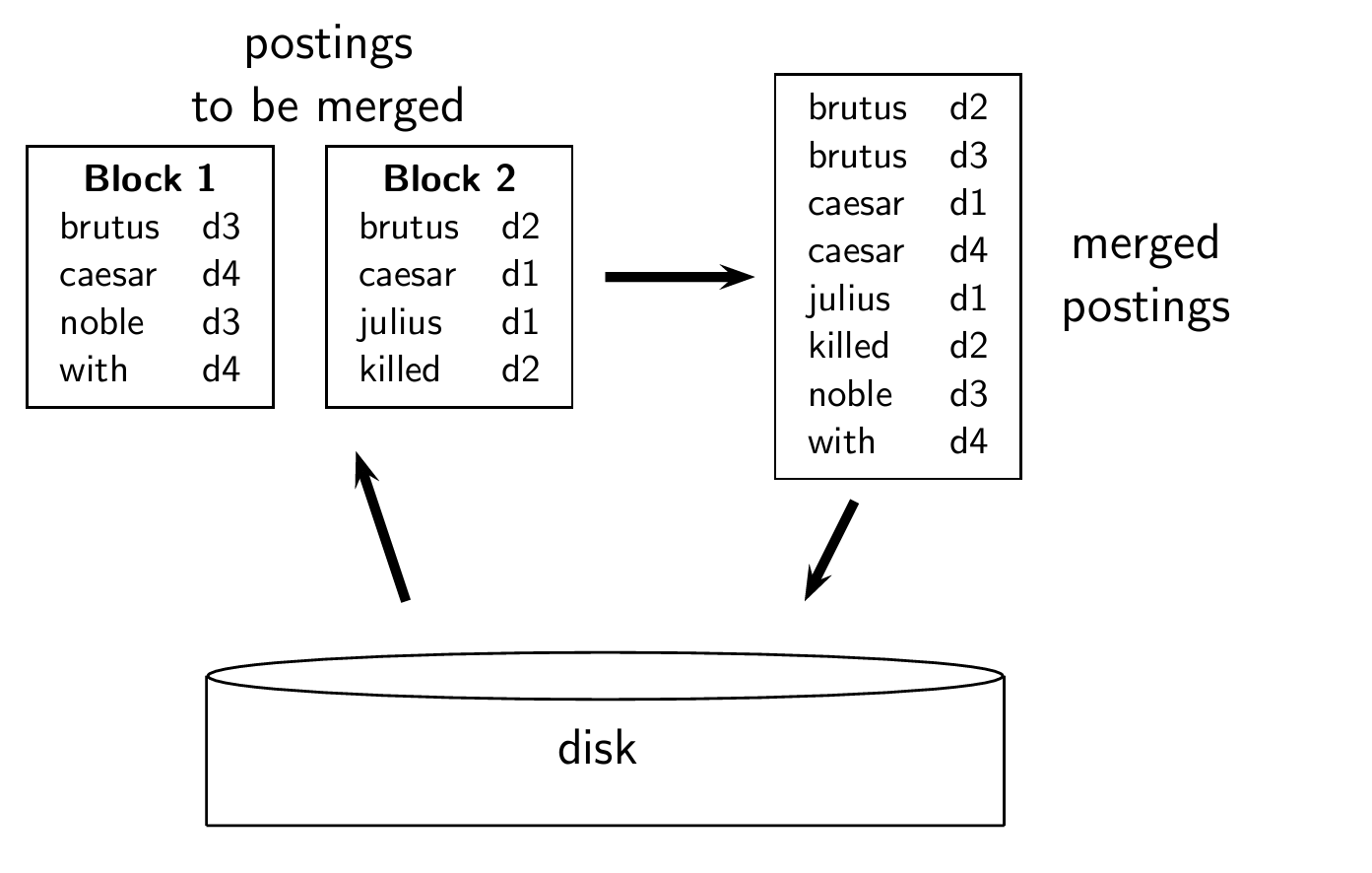
각 블록들을 메모리상에서 정렬한 후, 병합하여 disk에 쓴다.
Blocked Sort-Based Indexing

알고리즘은 사진과 같다.
각 블록에 대해 BSBI-INVERT를 수행하고, DISK에 쓰는 작업을 반복한 후, 정렬된 블록을 병합한다.
4. SPIMI algorithm
Problem with sort-based algorithm
그런데 BSBI에도 문제가 있다.
딕셔너리를 메모리에 유지해야 한다는 가정이 있어야 한다.
term-termID 매핑을 구현하려면 동적으로 확장 가능한 사전이 필요하다.
사실, 우리는 termID, docID postings 대신 term, docID postings를 활용하고 있다.
그런데 이렇게 하면 중간 파일이 정말 커지게 된다.
=> 확장은 하지만, 매우 느린 인덱스 구성 방법을 사용하게 된다.
Single-pass in-memory indexing
줄여서 SPIMI라고 부른다.
핵심 아이디어가 2가지 있다.
1. 각 블록에 대해 별도의 사전을 생성하면, 블록 간 termID 매핑을 유지할 필요가 없다.
2. 정렬하지 않는다. 게시글 목록에 게시글이 발생하는 대로 누적한다.
이 두 가지 아이디어로 각 블록에 대해 완전한 inverted index를 생성할 수 있다.
그런 다음 이러한 개별 인덱스를 하나의 큰 인덱스로 병합할 수 있다.
여기까지는 무슨 소리인지 싶다.
SPIMI-Invert

알고리즘은 위와 같다.
- index 정보를 담을 NEW FILE을 생성한다.
- term과 postings list를 매핑하는 데 사용할 NEW HASH table을 생성한다.
- 메모리가 충분한 동안 아래 과정을 반복한다.
- 토큰 스트림에서 다음 토큰을 가져온다.
- 해당 토큰이 해시 테이블(이하 딕셔너리)에 없으면, 이를 딕셔너리에 추가하고 해당 용어의 새로운 postings list를 생성한다.
- 해당 토큰이 이미 해시 테이블에 있으면, 해당 용어의 기존 postings list를 가져온다.
- postings list가 가득 차면, 크기를 두 배로 늘린다.
- postings list에 문서 ID를 추가한다.
- 모든 토큰을 처리한 후, 해시 테이블에 있는 용어들을 정렬한다.
- 정렬된 용어와 posting list를 디스크에 쓰기 위한 블록으로 저장한다.
- output_file을 반환한다.
여기서 블록을 병합하는 과정은 BSBI와도 유사하다.
SPIMI: Compression
Compression(압축)은 SPIMI를 더욱 효율적으로 만든다.
- Compression of terms
- Compression of postings
자세한 건 5장에서 다룬다.
5. Distributed indexing
Distributed indexing
웹 스케일 인덱싱의 경우, 분산 컴퓨터 클러스터를 사용해야 한다.
개별 컴퓨터는 결함이 발생하기 쉽다. -> 예기치 않게 속도가 느려지거나 실패할 수 있다.
이러한 컴퓨터의 풀을 어떻게 활용할 수 있을까?
=> 인덱싱 작업을 지시하는 마스터 머신을 유지한다.
이는 안전한 것으로 간주된다.
인덱싱을 parallel tasks(병렬 작업) 세트로 나눈다.
마스터 머신은 풀에서 idle machine(유휴 머신)에 각 작업을 할당한다.
Google data centers (2007 estimates; Gartner)
예시로 구글 데이터 센터를 들어보자.
구글 데이터 센터에는 상용 머신들이 있다.
그리고 이러한 데이터 센터는 전 세계에 분산되어 있다.
1백만 대의 서버와 3백만 개의 프로세서/코어가 존재한다고 한다. 지금은 2024년이니 당연히 배로 있을 것이다.
구글은 매 분기마다 100,000대의 서버를 설치한다고 한다.
이는 연간 2억~2억 5천만 달러의 지출을 차지한다고 하고, 전 세계 컴퓨팅 용량의 10%를 차지한다.
1000개의 노드가 있는 무중단 시스템에서 각 노드의 가동률이 99.9%인 경우, 시스템의 가동률은 얼마인가? (고장을 허용하지 않는다고 할 때.)
-> 37%이다. 99.9^1000 하면 0.37이 나온다.
서버가 1백만 대 설치되어 있는 경우, 3년마다 한 대의 서버가 고장난다고 할 때, 시스템 장애 간격은 얼마나 되는가?
-> 2분 미만이다.
이번에도 클로드가 계산해주었다.
서버의 수명이 3년이라는 것은 한 대의 서버가 고장 나는 데 평균 3년이 걸린다는 의미입니다.
100만 대의 서버가 있으므로, 전체 시스템에서는 (1,000,000 / 3) 대의 서버가 매년 고장 납니다.
연간 고장 나는 서버 수 = 1,000,000 / 3 = 333,333대
일 년은 약 525,600분입니다. 따라서 서버 고장 간격은 다음과 같이 계산할 수 있습니다.
서버 고장 간격 = 525,600분 / 333,333대 ≈ 1.58분
따라서 100만 대의 서버가 설치된 경우, 평균적으로 2분 미만의 간격으로 서버 고장이 발생하게 됩니다.
Parallel tasks
두 세트의 parallel task를 정의하고 이를 해결하기 위해 두 가지 유형의 머신을 배포할 것이다.
- parser
- inverter
우선 입력 문서 컬렉션을 분할로 나눈다.
(BSBI/SPIMI의 블록에 해당)
각 split(분할)은 문서의 하위 집합이다.
Parsers
-
Master의 역할:
마스터 머신은 한 split을 하나의 유휴 상태 parser 머신에 할당한다. -
Parser의 처리 과정:
할당받은 Parser(구문 분석기)는 한 번에 문서 하나를 읽고, 그 문서 내에서 (term, docID) 쌍을 생성한다. 이 쌍은 검색 색인에 사용될 수 있는 기본 데이터 요소이다. -
Parser의 출력 분할:
생성된 (term, docID) 쌍은 'j'개의 용어 파티션으로 작성된다.
각 파티션은 특정 범위의 용어의 첫 글자를 기준으로 분할된다.
예를 들어 j=3이라고 하면, a-f, g-p, q-z 이렇게 3 개의 파티션으로 나누어진다.
Inverters
parser에 의해 생성된 term-partition 쌍을 수집하고, 특정 용어 파티션에 대해 이들을 정렬하고, postings lists로 작성한다.
한 term partition은 특정 알파벳 범위의 용어들을 의미한다. (a-f 등)
- (term, docID) 쌍 수집
한 용어 파티션에 대해 모음. 예를 들어 한 inverter는 a-f 파티션에 속하는 쌍만 담당하여 받는다. - 정렬
수집된 (term, docID) 쌍을 용어별로 정리함. - 게시글 목록 작성
정렬된 쌍들을 기반으로 게시물 목록을 작성함. 게시물 목록은 각 용어가 문서 세트 내에서 출현한 위치들의 리스트임.
Data flow
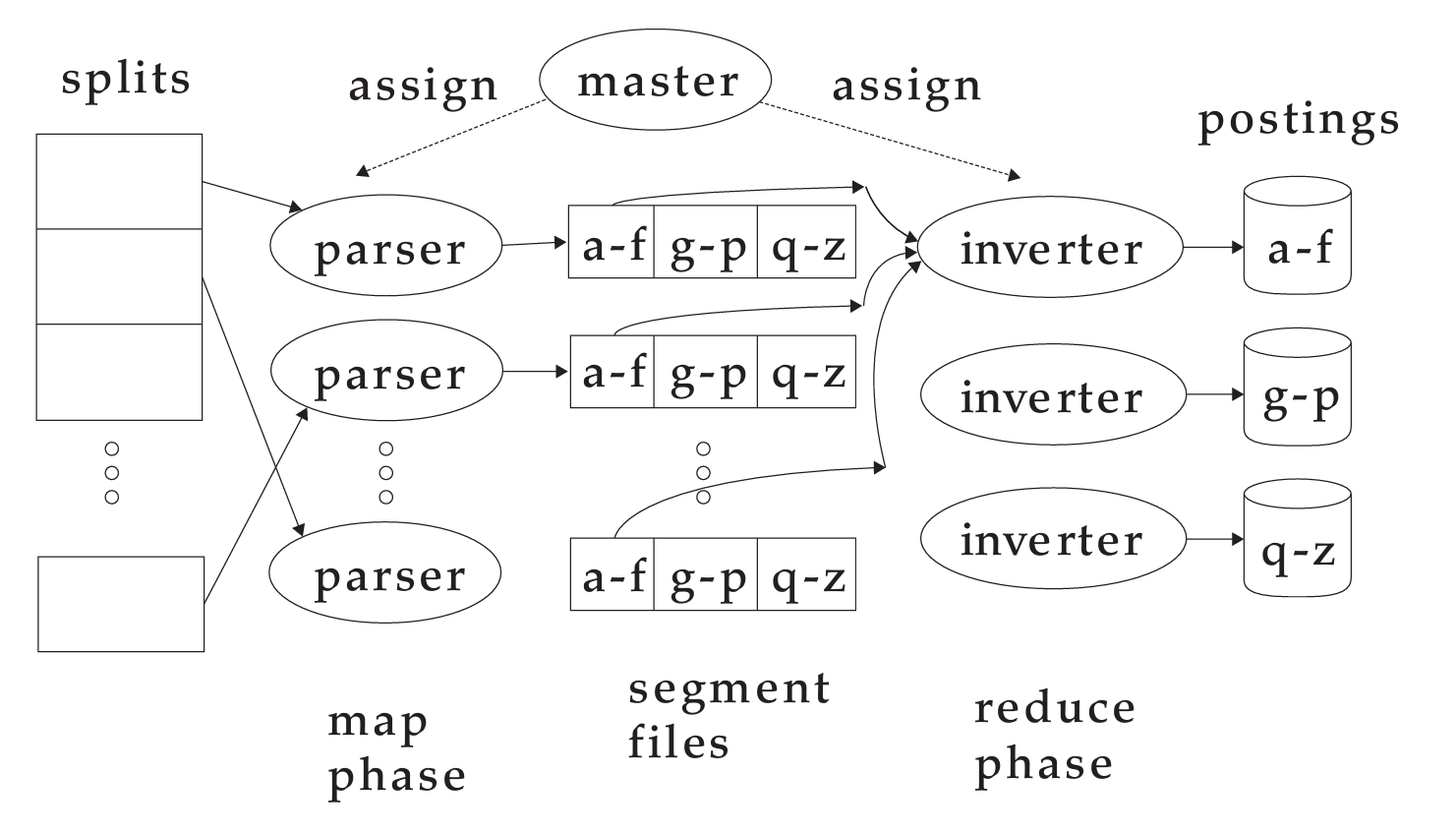
MapReduce
지금까지 설명한 index construction 알고리즘은 MapReduce의 인스턴스이다.
MepReduce는 분산 컴퓨팅을 위한 강력하고 개념적으로 간단한 프레임워크이다. 배포 시 코드를 더 작성할 필요도 없다.
당장 Google indexing system(2002년경)의 각 단계도 MapReduce로 구현되었다.
그리고 Index construction 말고, term-partitioned 인덱스를 document-partitioned 인덱스로 변환하는 단계도 있다.
왜 document-partitioned index가 더 나을까?
Index construction in MapReduce

MapReduce는 map, reduce 함수로 구성된다.
MapReduce 색인 구축의 과정:
Map 함수: Parser에 해당
입력으로 웹 컬렉션(문서들의 집합)을 받습니다.
각 문서를 처리하며 (용어, 문서ID) 쌍을 생성합니다.
예를 들어, 문서 d1에서 "C CAME", 문서 d2에서 "C DIED"라는 텍스트가 있다면, 이를 ((C, d2), (DIED, d2), (C, d1), (CAME, d1))와 같이 (용어, 문서ID) 쌍으로 매핑합니다.
Shuffling:
Map 함수의 출력이 셔플링 과정을 거쳐 같은 용어를 가진 쌍들이 reduce 함수로 전달되도록 합니다.
Reduce 함수: Inverter에 해당
map 함수의 출력에서 같은 용어를 키로 가진 (용어, 문서ID) 쌍의 리스트를 받습니다.
이 리스트를 용어별로 정렬하고, 각 용어에 대한 게시물 목록(postings lists)으로 변환합니다.
예를 들어, ((C, (d2, d1)), (DIED, (d2)), (CAME, (d1)))과 같은 출력을 생성합니다. 여기서 C는 두 문서 d1, d2에서 발견되었고, DIED는 d2에서, CAME는 d1에서 발견되었습니다.
예시에서:
"C"라는 용어는 두 문서 d1, d2에 나타났으며, 이에 대한 postings list는 (d2, d1)이 됩니다.
"DIED"라는 용어는 문서 d2에 나타났으며, 이에 대한 postings list는 (d2)입니다.
"CAME"라는 용어는 문서 d1에 나타났으며, 이에 대한 postings list는 (d1)입니다.
Exercise
- Master가 Parser에게 제공하는 작업 설명
=> 작업을 처리할 문서의 위치, 데이터 블록에 대한 정보
=> 문서를 처리하여 (term, docID) 쌍을 추출해야 하는 작업 범위나 파티션에 대한 세부 사항 - Parser가 Master에게 작업 완료 후 보고하는 정보
=> 처리된 문서의 (term, docID) 쌍
=> 처리한 문서 수, 용어의 수 같은 통계 정보 - Master가 Inverter에게 주는 작업
=> 처리할 용어 파티션에 대한 정보 (a-f 등)
=> 정렬하고 postings list로 만들어야 하는 (term, docID) 쌍들 - Inverter가 Master에게 작업 완료 후 보고하는 내용
=> 생성 및 정렬된 postings list의 상세 내용
=> 처리된 term의 수와 postings list가 쓰여진 파일이나 데이터 위치에 대한 정보
6. Dynamic indexing
Dynamic indexing
지금까지는 컬렉션이 정적이라고 가정하였다.
그런데 사실 컬렉션은 정적인 경우가 거의 없다.
문서들이 삽입, 삭제, 수정되는 경우가 많기 때문이다.
즉, 딕셔너리와 postings lists는 동적으로 수정되어야 한다.
Dynamic indexing: Simplest approach
가장 간단한 접근법은 아래와 같다.
- 큰 메인 인덱스 유지
- 새 문서를 작은 보조 인덱스에 추가: 새로 들어오는 문서들은 메모리 내의 작은 auxiliary index(보조 인덱스)에 추가한다. 메인 인덱스보다 훨씬 빠르게 업데이트될 수 있다.
- 두 인덱스에서 검색하고 결과 병합: 검색을 수행할 땐 메인 인덱스와 보조 인덱스 모두에서 검색을 수행하고, 두 결과를 병합하여 최종 결과를 제공한다.
- 삭제 처리
- 문서가 삭제될 때, 삭제된 문서에 대해 invalidation bit-vector (무효화 비트 벡터)를 사용한다. 이 벡터는 삭제된 문서의 식별자를 표시한다.
- 인덱스에서 반환된 문서 목록을 필터링할 때, 이 비트 벡터를 사용하여 삭제된 문서를 결과에서 제외한다.
Issue with auxiliary and main index
메인 인덱스와 보조 인덱스 간에는 당연히 문제가 생긴다.
잦은 병합도 문제가 될 수 있고,
병합 기간 동안의 낮은 검색 성능도 문제가 있다.
이를 해결하기 위해 Logarithmic merge라는, 좀 더 복잡한 것을 도입한다.
Logarithmic merge
로그라믹 결합은 index를 효율적으로 관리하는 방법 중 하나이다.
-
비용 분산: index 병합의 비용을 시간에 걸쳐 분산하므로, 단일 병합 작업으로 인한 시스템 부담을 줄일 수 있다.
-
색인 시리즈 유지: 여러 개의 색인을 유지하고, 각 색인은 이전 색인보다 크기가 두 배인 시리즈를 형성한다.
-
메모리 내 최소 색인 유지: 가장 작은 색인(Z0)을 메모리에 유지하여 빠른 업데이트와 접근을 가능하게 한다.
-
만약 Z0이 너무 크면, 디스크에 I0 이런 식으로 저장한다.
-
이미 디스크에 I0가 존재한다면, Z0와 I0를 병합하여 I1을 만든다.

LMERGEADDTOKEN
Z0에 새 토큰을 병합합니다. Z0는 메모리 내의 인덱스입니다.
만약 Z0의 크기가 특정 임계값 n에 도달하면, 다음 단계로 넘어갑니다.
무한 루프를 시작하며, 모든 인덱스 Ii에 대해 다음 작업을 수행합니다.
만약 현재 인덱스 Ii가 존재한다면 (즉, indexes 집합에 있다면),
현재 인덱스 Ii와 Zi를 병합하여 새로운 임시 인덱스 Zi+1를 생성합니다. 이 인덱스는 디스크 상에 저장됩니다.
Zi+1가 생성되었으므로, 이 인덱스를 indexes 집합에서 제거합니다.
만약 현재 인덱스 Ii가 존재하지 않는다면 (즉, 처음 병합하는 경우),
Ii를 현재 메모리 내 인덱스 Zi로 대체합니다.
Ii를 indexes 집합에 추가합니다.
병합을 중단하고 루프를 탈출합니다.
Z0를 비웁니다 (모든 토큰을 처리했으므로).
LOGARITHMICMERGE
Z0를 비웁니다; 이것은 메모리 내 색인입니다.
indexes 집합을 비웁니다; 이것은 디스크 상의 모든 색인을 추적합니다.
계속해서 진행되는 메인 루프를 시작합니다.
LMergeAddToken 함수를 호출합니다; 이 함수는 새로운 토큰을 처리하고 필요한 병합을 수행합니다.
이 알고리즘은 메모리 내의 인덱스가 커질 때마다 디스크에 저장된 색인과 병합하여, 색인의 크기가 지수적으로 증가하는 것을 방지하고, 인덱스의 크기가 관리 가능한 수준으로 유지된다.
이 방식은 인덱스의 병합 비용을 시간에 걸쳐 분산시키고, 시스템의 응답성을 유지하는데 도움을 준다.
Binary numbers: I3I2I1I0 = 2^32^22^1*2^0

Logarithmic merge
- 색인의 개수는 postings의 총 수 T에 대해 O(log T)로 제한된다.
- 쿼리를 처리할 때 O(log T) 개의 색인을 병합해야 한다.
- 시간 복잡도는 O(T log T)이다. T 개의 게시물 각각이 평균적으로 O(log T)번 병합되기 때문이다.
- 보조 색인(auxiliary index0의 구축 시간은 O(T^2)가 될 수 있다.
왜냐하면 각 게시물이 병합 과정에서 여러 번 조작될 수 있기 때문이다.
예를 들어 보조 색인이 크기 a를 가지고 있다면 사진같은 결론에 도달할 수도 있다.
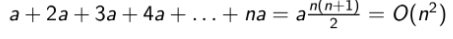
그러므로 logarithmic merge가 보조 인덱스 방식보다 훨씬 더 효율적이다.
Dynamic indexing at large search engines
거대한 검색 엔진에서 동적 인덱싱은 어떻게 될까?
- 종종 조합되어 사용된다.
- 잦은 incremental changes(증분 변경) 이 있다.
- 가끔씩 전체를 재구축해야하는데, 크기가 커질수록 더 어려워진다. Google은 전체 재구축이 아예 불가능할 수도 있다.
Building positional indexes
중간 데이터 구조가 크다는 점을 제외하면 기본적으로 동일한 문제이다.
※ 추가로 공부할 점
- RCV1 활용한 미니 프로젝트 해보기
- Logarithmic merge 완벽 숙지
