TIL - Tree, Graph, BST
저번시간에 이어서 오늘은 비선형구조에 해당하는 Tree, Graph에 대하여 학습한다.
1. Graph
[정의]
여러개의 점(정점)들이 간선들로 복잡하게 연결되어 있는 관계를 표현한 자료구조이다.
[특징]
루트 노드가 없으며, 자식-부모 관계가 존재하지 않는다.
사이클이 존재할 수 있다.
복잡한 네트워크 망과 같은 모습이다.
[어디에]
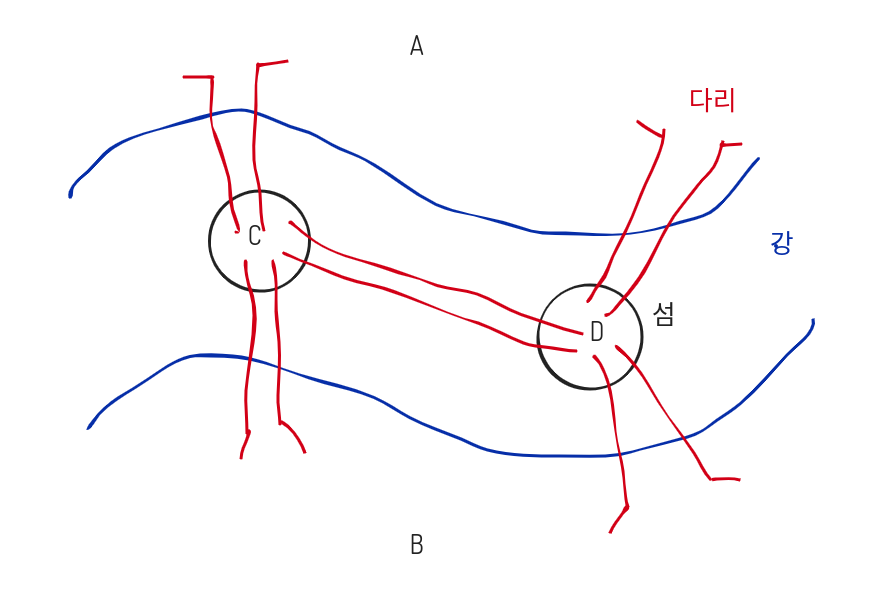
두 지역(A,B)과 두 개의 섬(C,D) 사이로 강물이 흐르고 이 때 구분된 4개의 지역을 잇는 5개의 다리가 있다고 가정해보자. 이 형태를 그래프에 적용시키면 4개의 지역을 정점(vertex), 5개의 다리를 간선(edge)으로 표현할 수 있다.
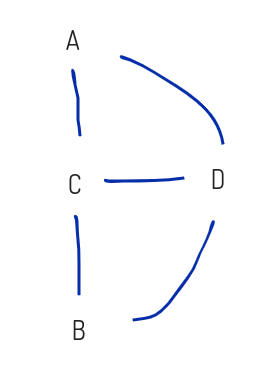
[종류]
1) 무향그래프
간선의 방향이 없는 그래프이다.
위에서 예제로 들었던 그래프와 같은 형태이다.
2) 유향그래프
간선의 방향이 있는 그래프이다.
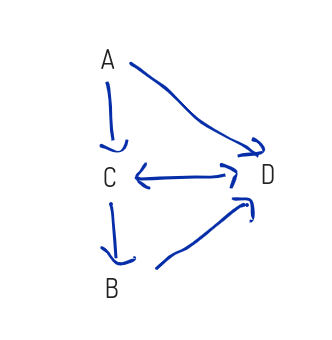
3) 가중치 그래프
정점을 연결하는 간선에 가중치를 할당한 그래프이다.
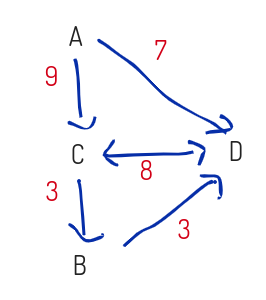
여기서 가중치란, 두 정점사이의 거리, 두 정점을 이동하는 데 걸리는 시간과 같은 정보가 될 수 있다.
[순회방법]
1) DFS (Depth-First Search)
깊이 우선 탐색이라고 한다.
하나의 경로를 끝까지 탐색한 후 찾지 못했다면 다음 경로로 넘어가 탐색하는 방법이다.
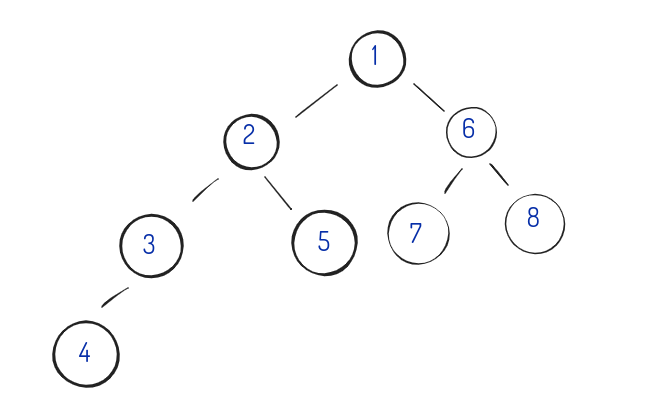
위와 같은 그래프에서 7을 찾는다고 생각했을 때
1 -> 2 -> 3 -> 4 -> 5 ->6 ->7 순서대로 찾는다.
2) BFS (Breadth-First Search)
너비 우선 탐색이라고 한다.
루트에서 가까운 지점부터 탐색을 한 후 찾지 못했다면 다음으로 떨어져있는 경로를 탐색하는 방법이다.
DFS에서와 같은 그래프에서 7을 찾는다고 생각했을 때
1 -> 2 -> 6 -> 3 -> 5 -> 7 순서대로 찾는다.
2. Tree
[정의]
노드와 각각의 노드를 연결시켜 주는 선분인 가지로 형성된 그래프이다.
[특징]
오직 하나의 루트 노드를 가지고있으며 자식-부모 관계가 존재한다.
사이클이 존재할 수 없다.
계층형 구조를 띄고 있다.
[어디에]
몇 주전 우리가 만들었던 카페 메뉴판도 트리 구조로 되어있다.

음식 카테고리 안에 빵, 케이크 등 여러개의 음식이 있고 또 그 안에 음식의 종류 들이 들어가있다.
모두 하나의 카테고리에서 시작되어 가지처럼 뻗어나가는 형태로 되어있다.
이 형태를 우리는 트리구조라고 한다.
[종류]
1) 이진트리
자식 노드가 최대 두 개인 노드들로 구성된 트리를 말한다.
2) 이진 탐색 트리
이진 트리에 탐색조건이 더해진 트리이다.
모든 왼쪽 자식들은 루트나 부모보다 작은 값이고 모든 오른쪽 자식들은 루트나 부모보다 큰 값이라는 조건을 가지고 있다.
하지만 이진 탐색 트리는 균형 잡힌 트리가 아닐 때 입력되는 값의 순서에 따라 한쪽으로 노드가 몰릴 가능성이 있다. 그렇게되면 트리의 높이는 점점 커지고 그에 따라 검색에 오랜 시간이 걸릴 가능성이 있다. 이 때문에 균형 이진 탐색 트리 라는 것이 나왔다.
3) 균형 이진 탐색 트리
이진 탐색 트리의 문제점을 보완하기 위해 나온 트리이다.
왼쪽 노드와 오른쪽 노드의 높이 차이가 1 이하이다.
이를 유지하기 위해 삽입과 삭제마다 트리의 구조를 재조정하는 과정을 거친다.
[순회방법]
모든 방법은 루트를 기준으로 진행한다. 또한 왼쪽노드를 먼저 순회한 후 오른쪽 노드를 순회한다.
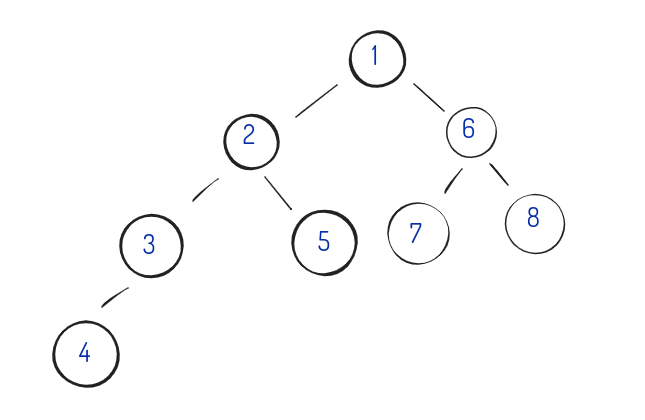
1) 전위 순회
루트를 가장 먼저 순회하는 방법이다. => Root - Left - Right
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8
2) 중위 순회
루트를 중간에 순회하는 방법이다. => Left - Root - Right
4 -> 3 -> 2 -> 5 -> 1 -> 7 -> 6 -> 8
3) 후위 순회
루트를 나중에 순회하는 방법이다. => Left - Right - Root
4 -> 3 -> 5 -> 2 -> 7 -> 8 -> 6 -> 1
오늘은 Tree, Graph와 그 특징에 대하여 공부하였다.
내일은 이를 바탕으로 알고리즘 문제를 푼다.
벌써부터 어려울거같은 느낌이 들지만... 화이팅!
오늘은 여기까지!!