나는 프로그래머스에서 문제를 많이 풀었다. 프로그래머스는 딱히 알고리즘 분류가 되어있지 않은데...아무거나 골라잡아 풀다보니 구현,그래프 문제만 왕창 푼 것 같다. 아무튼 최근에는 웰노운이지만 코테에는 잘 안나와서(나오긴 하지만 구현,그래프보단 비중 적음) 소홀해진 알고리즘을 볼려고 한다. 평소에 알고리즘은 눈으로 슥 보고 음~그렇군 하고 넘어가는데..아무래도 이렇게 하니까 기억에서 증발되는 경우가 많은 것 같다. 그나마 블로그에 적으면 장기기억이 되는 듯하고, 오늘 볼 배낭 문제는 유명한 문젠데 척 보고 뭔소리야?가 절로 나왔던 문제이기 때문에...반성하며 블로그에 정리해본다.
직접 풀어보자.
백준 12865을 보며 공부해보자. 아주 클래식한 배낭 문제이다. 참고로 배낭에 넣을 물품을 쪼갤 수 있는 경우에는 그리디로 풀 수 있는데, 이 문제의 경우에는 물품을 쪼갤 수 없으므로(0-1 배낭문제) dp로 풀어야 한다.
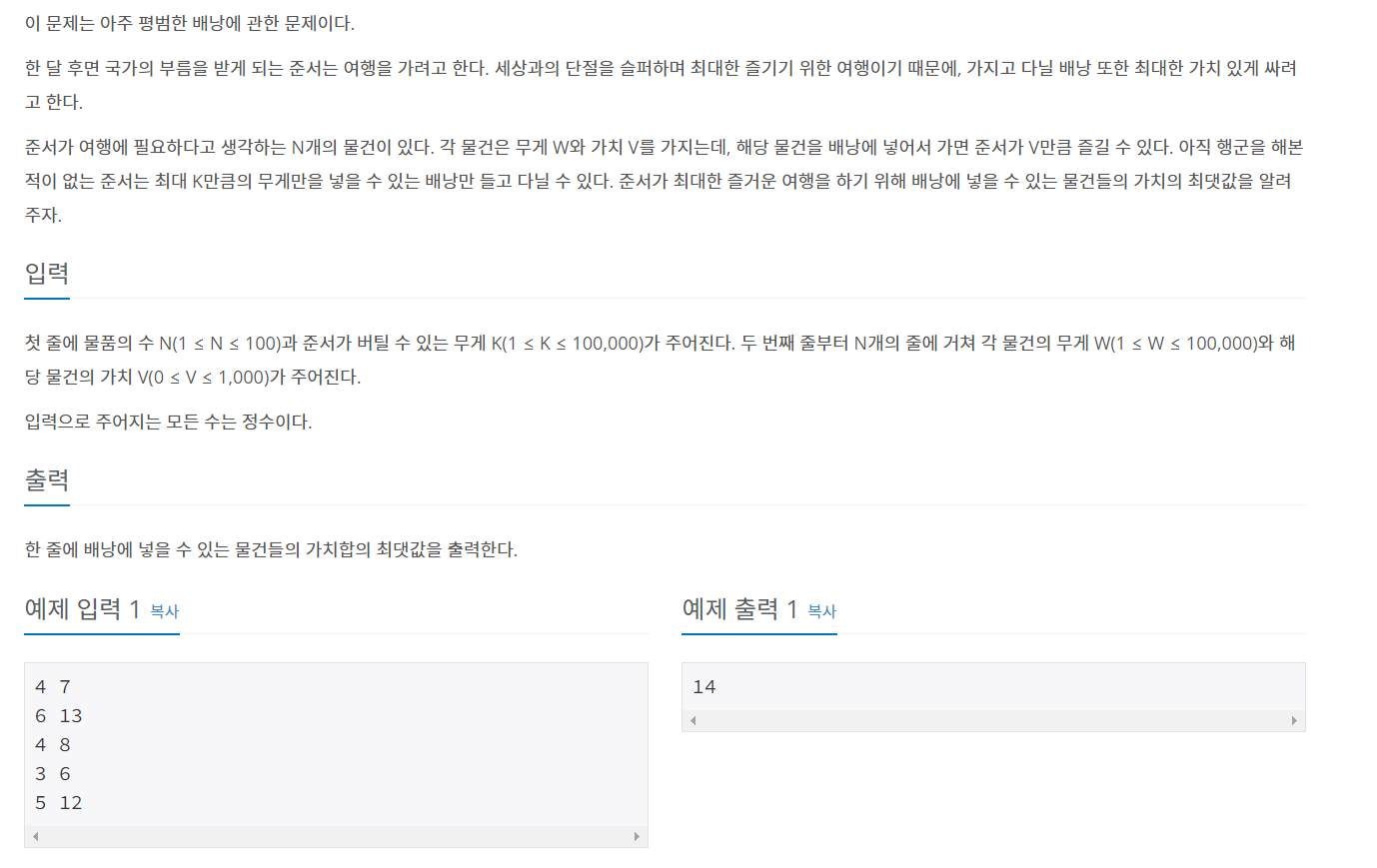
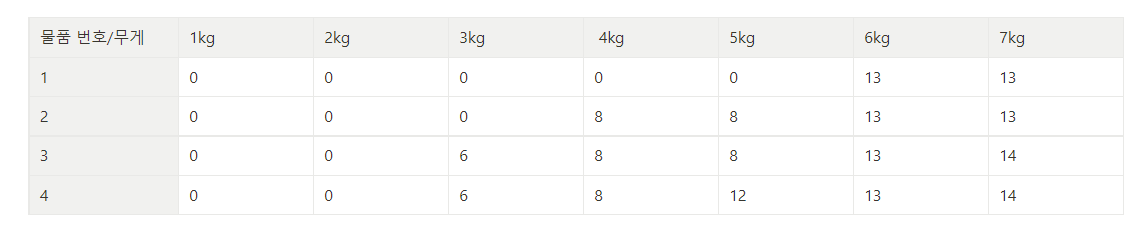
잘 알려진 문제다 보니 검색하면 풀이법이 많이 나온다. 이런 그래프가 많이 나온다. 이 그래프가 어떻게 나왔는지 알아보자.
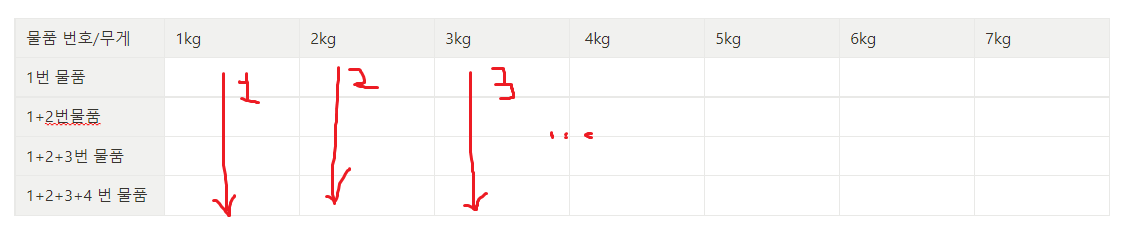
먼저 물품번호의 뜻은 다음과 같다. i번째 물품을 추가했을때 어떻게 되느냐...를 의미한다고 보면 된다. 세로 순서로, 무게가 작은 순으로 채워 나간다. (위 그림에 표시한 순서대로)
추가할 i번째 물품이 무게 제한 w보다 무겁다면 그냥 dp[i-1]를 가져오면 될 것이다.(바로 위의 값) 그렇지 않다면,
- i번째 보석을 일단 넣고, 무게제한w에서 i무게를 뺐을때의 무게 k에서 서의 최적값을 테이블에서 가져와서 더하기
- i번째 보석을 넣지 않고, dp[i-1]의 값 (바로 위의 값)을 가져오기
둘 중에서 더 가치가 큰 경우를 선택하면 될 것 이다.

한 칸을 잡고 예를 들면 다음과 같다. 13과 14를 비교하면 14가 더 크므로 14를 채워 넣는다.

위 그래프 채워넣는 로직을 점화식으로 세우면 다음과 같다.
n,k=list(map(int,input().split()))
items=[(0,0)]
W=[0]
V=[0]
for i in range(n):
w,v=list(map(int,input().split())) #무게,가치
W.append(w)
V.append(v)
dp=[[0]*(k+1) for _ in range(n+1)]
for item in range(1,n+1):
for kg in range(1,k+1):
if W[item]>kg:
dp[item][kg]=dp[item-1][kg]
else:
dp[item][kg]=max(dp[item-1][kg], V[item]+dp[item-1][kg-W[item]])
print(dp[n][k])참고: https://st-lab.tistory.com/141
https://velog.io/@lre12/%EB%B0%B1%EC%A4%80-12865%EB%B2%88-%ED%8F%89%EB%B2%94%ED%95%9C-%EB%B0%B0%EB%82%AD

