📌 문제 058) K번째 최단 경로 찾기
시간 제한 2초, 플래티넘, 백준 1854번
봄캠프를 마친 김진영 조교는 여러 도시를 돌며 여행을 다닐 계획이다. 그런데 김 조교는, '느림의 미학'을 중요시하는 사람이라 항상 최단경로로만 이동하는 것은 별로 좋아하지 않는다. 하지만 너무 시간이 오래 걸리는 경로도 그리 매력적인 것만은 아니어서, 적당한 타협안인 'k번째 최단경로'를 구하길 원한다. 그를 돕기 위한 프로그램을 작성해 보자.
입력
첫째 줄에 n, m, k가 주어진다. (1 ≤ n ≤ 1,000, 0 ≤ m ≤ 2,000,000, 1 ≤ k ≤ 100) n과 m은 각각 김 조교가 여행을 고려하고 있는 도시들의 개수와, 도시 간에 존재하는 도로의 수이다.
이어지는 m개의 줄에는 각각 도로의 정보를 제공하는 세 개의 정수 a, b, c가 포함되어 있다. 이것은 a번 도시에서 b번 도시로 갈 때는 c의 시간이 걸린다는 의미이다. (1 ≤ a, b ≤ n, 1 ≤ c ≤ 1,000)
도시의 번호는 1번부터 n번까지 연속하여 붙어 있으며, 1번 도시는 시작도시이다. 두 도로의 시작점과 도착점이 모두 같은 경우는 없다.5 10 2 # 도시 수, 도로 수, K 1 2 2 1 3 7 1 4 5 1 5 6 2 4 2 2 3 4 3 4 6 3 5 8 5 2 4 5 4 1
출력
n개의 줄을 출력한다. i번째 줄에 1번 도시에서 i번 도시로 가는 k번째 최단경로의 소요시간을 출력한다.
경로의 소요시간은 경로 위에 있는 도로들을 따라 이동하는데 필요한 시간들의 합이다.
i번 도시에서 i번 도시로 가는 최단경로는 0이지만, 일반적인 k번째 최단경로는 0이 아닐 수 있음에 유의한다. 또, k번째 최단경로가 존재하지 않으면 -1을 출력한다. 최단경로에 같은 정점이 여러 번 포함되어도 된다.-1 10 7 5 14
1단계 문제 분석
- 시작점과 도착점이 주어지고 이 목적지까지 가는 K번째 최단 경로를 구하는 문제이다.
- 도시(노드)의 개수는 1,000개, 도로(에지)의 수는 2,000,000이면서 시간 제약이 2초이므로 다익스트라 알고리즘으로 접근하자.
- 이 문제에서 가장 고민되는 부분은 최단 경로가 아니라 K번째 최단 경로라는 것이다.
[K번째 최단 경로 해결 방법]
- 최단 경로를 표현하는 리스트를 K개의 row를 갖는 2차원 리스트 형태로 변경하고자 한다.
- 기존 다익스트라 로직에서 사용한 노드를 방문 리스트에 체크해 두고, 다음 도착 시 해당 노드를 다시 사용하지 않도록 설정하는 부분은 삭제해야 한다. K번째 경로를 찾기 위해서는 노드를 여러 번 쓰는 경우가 생기기 때문이다.
- 주어진 예제 데이터 기반으로 그래프를 그린다. 도시는 노드로, 도로는 에지로 나타낸다.
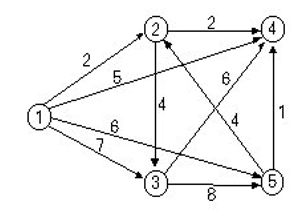
- 변수를 선언하고, 그래프 데이터를 받는 부분은 모두 다익스트라 알고리즘 준비 과정과 동일하다.
- 유일하게 다른 점은 최단 거리 리스트를 1차원이 아닌 K개의 row를 갖는 2차원 리스트로 선언한다는 것이다. 최단 거리 리스트는 최초 시작 노드의 첫 번째 경로는 0, 그 외의 경로는 모두 무한대로 초기화한다. 그 후, 다음에서 설명하는 규칙을 토대로 거리 리스트를 채운다.
[최단 거리 리스트 채우기 규칙]
1) 우선순위 큐에서 연결된 노드와 가중치 데이터를 가져온다.
2) 연결 노드의 K번째 경로와 신규 경로를 비교해 신규 경로가 더 작을 때 업데이트한다. 이때, 경로가 업데이트되는 경우 거리 배열을 오름차순으로 정렬하고 우선순위 큐에 연결 노드를 추가한다.
3) 1~2번 과정을 우선순위 큐가 비워질 때까지 반복한다. K번째 경로를 찾기 위해 노드를 여러 번 방문하는 경우가 있으므로 기존 다익스트라의 방문 노드를 체크하여 재사용하지 않는 로직은 구현하지 않는다.
- 최단 거리 리스트를 탐색하면서 K번째 경로가 무한대면 -1을 출력하고, 그 외에는 해당 경로 값을 출력한다.
2단계 슈도 코드
N(노드 개수), M(에지 개수) K(몇 번째 최단 경로를 구해야 하는지 나타내는 변수)
W(그래프 정보 저장 인접 리스트)
distance(거리 저장 리스트) # 충분히 큰 수로 초기화
for 에지 개수만큼 반복:
인접 리스트에 에지 정보 저장
우선순위 큐에 시작 노드 저장 # 1번 노드 거리 0으로 저장
시작 도시 최단 거리 저장 # 시작점이기 때문에 0으로 저장
# 다익스트라 수행
while 큐가 빌 때까지:
우선순위 큐에서 데이터 가져오기 (거리, 노드)
for 현재 노드에서 연결된 에지 탐색:
새로운 총 거리 = 현재 노드의 거리 + 에지 가중치
if 새로운 노드의 K번째 최단거리 > 새로운 총 거리:
새로운 노드의 K번째 최단 거리를 새로운 총 거리로 변경하고 거리 순으로 정렬
우선순위 큐에 새로운 데이터 추가 (거리, 노드)
for 노드 개수:
# 다음은 최초 값이라면 K번째 거리가 없다는 뜻
if 각 노드의 거리 리스트에 K번째 값이 최초 설정 값:
-1 출력
else: K번째 값 출력3단계 코드 구현
import sys
import heapq
input = sys.stdin.readline
N, M, K = map(int, input().split())
W = [[] for _ in range(N + 1)]
# 거리 리스트를 충분히 큰 값으로 초기화
distance = [[sys.maxsize] * K for _ in range(N+1)]
for _ in range(M):
a, b, c = map(int, input().split())
W[a].append((b, c))
pq = [(0, 1)] # 가중치 우선이기 때문에 가중치, 목표 노드 순서로 저장
distance[1][0] = 0
while pq: # 변형된 다익스트라 수행
cost, node = heapq.heappop(pq)
for nNode, nCost in W[node]:
sCost = cost + nCost
if distance[nNode][K-1] > sCost:
distance[nNode][K-1] = sCost
distance[nNode].sort()
heapq.heappush(pq, [sCost, nNode])
for i in range(1, N+1):
if distance[i][K-1] == sys.maxsize:
print(-1)
else:
print(distance[i][K-1])
