이 글은 [파이썬과 케라스로 배우는 강화학습]을 기반으로 작성되었습니다.

시작하며

2021년 여름, 활동중인 데이터 사이언스 학회에서 강화학습을 공부를 시작합니다. 세션을 통해 습득한 내용 + 나름대로 의미있게, 재미있게 읽은 책의 내용을 두달간 기록합니다.

글을 쓰는 사람은 강화학습 선수지식이 '전혀' 없는 상태로 강화학습에 입문했습니다. 앞으로 관련 포스팅을 이어가며 부족한 부분이 많이 보일텐데, 부족한 머리를 싸매가며 이해한 바를 토대로 작성한 것이니 내용상 지적할 점이 많더라도 양해 부탁드립니다😘

강화학습의 개념

행동심리학과 강화학습, 머신러닝과 강화학습에 대하여

강화학습의 개념을 이해하려면 먼저 행동심리학과 강화학습의 연관성, 그리고 ML과 강화학습의 연관성에 대해 이해해야 합니다.

행동심리학과 강화학습

1930년대 행동주의 심리학자 '스키너'는 '강화'라는 개념을 처음으로 제시합니다. 스키너는 쥐 실험을 통해 '쥐는 지렛대를 누르면 먹이를 먹을 수 있다는 것을 "학습"한다는 것'을 확인합니다. 지렛대와 먹이 사이의 상관관계를 모르던 쥐는 우연히 상자 안에 있는 지렛대를 누른 이후 보상(먹이)이 나오는 것을 확인하고 점점 지렛대를 자주 누르게 됩니다. 즉 쥐는 보상을 통해 행동과 행동의 결과를 연결할 수 있게 된다는 것입니다. 일종의 시행착오 학습이죠.

📌 스키너의 [조작적 조건화]에 대해서 자세히 알아보고 싶다면 클릭하세요! 본문에서는 다루지 않습니다.

머신러닝과 강화학습

머신러닝은 인공지능의 한 범주로서 컴퓨터가 그 스스로 학습하게 하는 알고리즘을 개발하는 분야입니다. 즉, 미리 프로그램 되어 있는 대로 작동하는 것이 아니고, 주어진 데이터를 토대로 스스로 성능을 높여가는 것을 말합니다. 머신러닝은 3가지 범주로 나눌 수 있습니다.

1. 지도학습

• 지도 학습은 정답이 있는 데이터를 활용해 컴퓨터를 학습시키는 것입니다. 입력 값과 입력값에 대한 Label(정답)을 주고, 컴퓨터는 자신이 낸 답과 정답의 차이를 감소시키는 방향으로 학습합니다.

2. 비지도학습

• 비지도 학습은 라벨이 없는 데이터를 통해 학습합니다. 데이터의 비슷한 특징 패턴을 찾아내고 군집화를 시도하여 새로운 데이터에 대한 결과를 예측합니다.

3. 강화학습

• 강화학습은 지도 학습, 비지도학습과는 성격이 다릅니다. 강화학습은 보상을 통해 학습하며, 보상은 컴퓨터가 선택한 행동에 대한 반응입니다. 즉, 이 보상은 지도 학습에서처럼 직접적인 정답은 아니지만, 컴퓨터에게는 간접적인 정답의 역할을 합니다. 지도학습에서 정답 데이터와의 오차를 줄여나가는 방식으로 학습하는 것처럼, 강화학습에서는 행동의 결과로 나타나는 보상을 통해 학습합니다. 가장 좋은 보상을 얻기 위해서!

📌 기계학습 machine learning, 지도학습 Supervised Learning, 비지도학습 Unsupervised Learning에 대해서 자세히 알아보고 싶다면 클릭하세요! 본문에서는 다루지 않습니다.

스스로 학습하는 컴퓨터, 에이전트 agent

이러한 강화학습을 통해 스스로 학습하는 컴퓨터, 즉 스키너 실험의 쥐처럼 '행동'하고 '보상'을 통해 학습하는 주체를 앞으로 에이전트(agent)라고 칭하겠습니다.

에이전트(행동 주체)는 환경에 대한 사전 지식이 없는 상태에서 학습을 합니다. 스키너의 쥐 실험에서 쥐가 지렛대와 먹이 사이의 상관관계를 몰랐던 것처럼 말이죠. 에이전트는 자신이 놓인 환경에서 오로지 자신의 상태(state)를 인식하고 행동(action)합니다. 그러면 환경은 보상(reward)과 에이전트의 행동으로 인해 변화한 다음 상태를 반환합니다. 에이전트는 반복적인 행동과 그로 인한 보상을 통해 어떤 행동이 더 좋은 행동인지를 학습하게 됩니다.

강화학습 문제

순차적 행동 결정 문제

그렇다면 강화학습은 어떠한 문제 상황에 적용해야 할까요? 강화학습은 '순차적 행동 결정 문제' 상황에 적용됩니다. 우리는 아무리 간단한 상황에서라도, 성공적으로 특정 태스크를 마치기 위해서는 몇 가지 의사결정을 순차적으로 해 주어야 합니다. 순차적 행동 결정의 상황에서는 어떤 행동(의사결정)을 하게 되면, 그로 인해 현 상황이 바뀌고, 바뀐 상황에서 행동(의사결정)을 하면, 또 다시 다음 상황이 바뀝니다. 즉 행동이 다음 상황에 영향을 주며, 순차적으로 행동을 잘 선택해야 하는 문제를 순차적 행동 결정 문제라고 합니다.

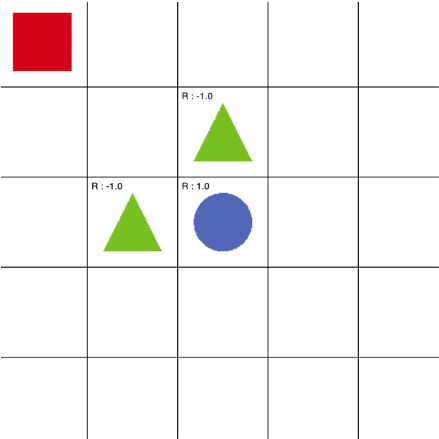
빨간 네모는 초록 세모를 피해 파란 동그라미에 도달해야 합니다. 이와 같은 상황에서, 빨간 네모가 한 칸씩 어느 방향으로 움직일지 의사결정을 할 수 있다면, 이것이 대표적인 순차적 행동 결정 문제에 해당합니다. 빨간 네모가 방향을 정해 한 칸을 움직이게 되면, 행동에 따라 현 상황이 바뀌고, 바뀐 상황에서 또 파란 동그라미에 도달하기 위해 의사결정을 해야하는 상황이기 때문입니다.

그렇다면, 순차적 행동 결정 문제를 어떻게 수학적으로 표현할 수 있을까요?

에이전트(컴퓨터)를 '강화학습'시켜 순차적 행동 결정 문제를 해결하려면, 순차적 행동 결정 문제를 수학적으로 표현하는 것이 가장 중요합니다. 당연하게도, 문제가 수학적으로 표현되지 않는다면 에이전트(컴퓨터)는 행동을 최적화할수도, 문제를 해결할 수도 없을 것입니다.

이 때 순차적으로 행동을 결정하는 문제를 수학적으로 정의할 때 사용하는 방법이 바로 MDP(Markov Decision Process) 입니다. MDP의 방식으로 문제를 정의하게 되면, 컴퓨터는 순차적 행동 결정 문제에 접근할 수 있게 됩니다. MDP와 벨만방정식에 대해서는 다음 포스팅에서 다룹니다.

순차적 행동 결정 문제의 구성 요소

에이전트를 강화학습 시키기 위해, 순차적 행동 결정 문제를 정의해봅시다. 순차적 행동 결정 문제는 총 4가지의 구성 요소로 정의할 수 있습니다.

1. 상태 state
2. 행동 action
3. 보상 reward
4. 정책 policy

• 상태 state
  현재 시점에서 상황이 어떤지를 나타내는 값의 집합입니다. 정확히 말하면, 에이전트가 관찰 가능한 상태의 집합 입니다. 상태에는 에이전트의 정적 요소 뿐만 아니라 동적 요소(ex 움직이는 속도, 가속도 등) 역시 당연하게 포함됨을 주의해야 합니다. 또한 상태는 시간에 따라 변화하게 됩니다.

• 행동 action
  에이전트가 취할 수 있는 행동의 집합입니다.

• 보상 reward
  에이전트가 학습을 할 수 있게 하는 유일한 정보로서, 에이전트가 한 '행동'에 대해 환경이 제공하는 피드백입니다. 보상을 통해 에이전트는 자신의 행동을 평가할 수 있습니다. 보상은 에이전트에 속하지 '않는' 환경의 일부이며, 따라서 에이전트는 어떤 상태와 행동에서 얼마의 보상이 나올지 미리 알 수 없습니다.

• 정책 policy
  순차적 행동 결정 문제에 있어 구해야 할 '답'입니다. 에이전트가 처한 모든 상태에 대해 어떤 행동을 해야하는지 정해놓은 것이 바로 정책입니다. 가장 좋은 정책을 최적 정책(optimal policy)이라고 하며, 최적 정책에 따라 행동한 에이전트는 보상의 합을 최대로 받습니다.

5x5 grid world 문제로 예를 들어 봅시다.

상태는 빨간 네모의 위치를 의미합니다. 상태집합은 다음과 같이 표현할 수 있습니다.
S= { (1,1),(2,1),(1,2),⋯, (5,5) }

행동은 빨간 네모가 어느 방향으로 한 칸 이동할지를 의미합니다. 행동 집합은 다음과 같이 표현할 수 있습니다.
A = {상, 하, 좌, 우}

보상은 양과 음으로 설정되어 있습니다. 예시에서는 초록 세모에 도달하면 -1.0의 reward가, 파란 동그라미에 도달하면 +1.0의 reward를 받게 됩니다.

다음 포스팅

에이전트를 강화학습 시키기 위해서는 이러한 '순차적 행동 결정 문제'를 수학적으로 정의해야 한다고 했습니다. 다음 포스팅에서는 순차적 행동 결정 문제를 수학적으로 정의할 때 사용하는 방법인 MDP(Markov Decision Process) 에 대해 포스팅 하겠습니다. MDP는 앞서 설명한 상태, 행동을 포함하여 보상 함수, 상태 변환 확률, 할인율까지 총 5개의 구성 요소로 이루어져 있습니다.

순차적 행동 결정 문제를 수학적으로 정의한 MDP, 에이전트가 어떤 정책이 더 좋은 정책인지 판단하는 기준인 가치함수, 현재 상태의 가치함수와 다음 상태 가치함수의 관계식인 벨만 방정식까지 다음 포스팅에서 다루도록 하겠습니다.