이 글은 [파이썬과 케라스로 배우는 강화학습]을 기반으로 작성되었습니다.

시작하며

지난 포스팅 에서는 강화학습의 개념과 순차적 행동 결정 문제에 대해 다루었습니다. 이번 포스팅에서는 MDP(Markov Decision Process)와 벨만방정식에 대해 다루겠습니다.

MDP의 구성요소

강화학습이 풀고자 하는 문제는 '순차적 행동 결정 문제'입니다. 강화학습이 풀고자 하는 이 순차적 행동 결정 문제는 MDP로 정의할 수 있습니다. 순차적 행동 결정 문제를 MDP로 전환해야, 가치함수를 벨만 방정식으로 계산해 최적 정책을 찾을 수 있습니다. 즉 순차적 행동 결정 문제의 답을 찾을 수 있습니다.

MDP를 통해 우리는 순차적 행동 결정 문제를 수학적으로 정의할 수 있습니다. 문제의 정의는 에이전트가 학습을 하는데에 있어 가장 중요한 단계라고 할 수 있습니다. 그럼 이렇게나 중요한 MDP의 구성요소에는 무엇이 있는지 알아봅시다!

상태

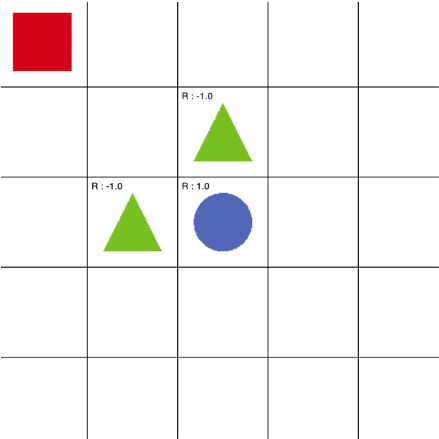
상태 S는 에이전트가 관찰 가능한 상태의 집합입니다. 위 그림과 같은 5x5 grid world 문제에서 상태는 모든 격자의 위치로서 총 25개가 있을 것입니다. 빨간색 네모가 에이전트인데, 에이전트가 그림과 같은 위치에 있다면 에이전트의 상태는 (1,1)이 됩니다. 그리고 5x5 grid world의 상태 집합은 S={(1,1),(1,2),(1,3),…,(5,5)} 가 됩니다.

에이전트는 시간에 따라 움직이며 25개의 상태 집합 안에 있는 상태들을 탐험하게 되며, 시간 t에서의 상태 S가 (1,2)라면 St = (1,2) 로 표현합니다.

행동

행동 A는 에이전트가 상태 St에서 할 수 있는 가능한 행동의 집합입니다. grid world 문제에서 행동의 집합은 A={up, down, left, right}으로 표현할 수 있으며, 시간 t에 에이전트가 특정한 행동 a를 했다면 At = a와 같이 표현할 수 있습니다.

보상함수

보상 R은 에이전트가 학습할 수 있는 유일한 정보입니다. 시간 t에서 상태가 s이고 행동이 a일 때, 에이전트가 받을 보상은 다음과 같은 수식으로 표현합니다.

r(s,a) = E [ Rt+1 | St = s , At = a ]
(상태가 St=s이고 그 상태에서의 행동이 At=a일 때(조건문, |로 표현), 받을 보상에 대한 기댓값 E.

보상 함수 r(s,a)는 상태 s에서 행동 a를 했을 때의 보상의 기대값을 수치로 반환합니다. 기댓값이란 일종의 평균이며 어떤 정확한 값이 아니라 나오게 될 숫자에 대한 예상입니다. 환경에 따라서 같은 상태에서 같은 행동을 취하더라도 다른 보상을 줄 수도 있으므로 보상함수는 기댓값으로 표현합니다.

또한 보상함수에서 중요한 것은 시점인데, 수식에서도 파악할 수 있듯 에이전트가 어떤 상태에서 행동한 것은 t시점인데(St, At) 보상을 받는 것은 t+1시점이라는 것입니다.(Rt+1)

이는 보상을 에이전트가 t시점에서 이미 알고 있는 것이 아니고, 행동을 한 후에 환경이 알려주는 것이기 때문입니다. 에이전트는 환경으로부터 하나의 시간 단위가 지난 다음에 보상을 받으며, 이 단위를 타임스텝이라고 합니다.

상태 변환 확률

에이전트가 행동을 취한다고 해서 모두 상태가 행동에 따라 그대로 변하는 것은 아닙니다. 에이전트가 상태 s에서 어떤 행동 a를 했을 때, 도달하는 다음 타임 스텝의 상태를 s'라고 합시다. s'는 상태 s에서 a를 했을 때 도달 할 수 있는 다음 상태를 의미합니다. 하지만 에이전트는 s'에 도달하지 못할 수도 있습니다. 앞으로 가는 행동 a를 취할 때, 바람이 불 수도 있고 넘어질 수도 있씁니다. 이처럼 상태의 변화에는 확률적 요인이 고려되어야만 합니다.

상태변환 확률은 다음과 같은 수식으로 표현할 수 있습니다.
Pass' = P [ St+1 = s' | St = s , At = a ]
(상태가 St=s이고 그 상태에서의 행동이 At=a일 때(조건문, |로 표현), 다음 시점 t+1에서 상태 s'에 도달할 확률)

이 값 역시 에이전트가 알지 못하는 값으로서 '환경'의 일부입니다. 상태변환확률은 환경의 모델 이라고도 합니다. 다이나믹 프로그래밍에서는 상태변환확률과 같이 에이전트가 알지 못하는 값들을 모두 알고 있어야만 계산이 가능합니다. 즉, 모델 프리하지 못합니다. 따라서 현실의 문제에 다이나믹 프로그래밍을 적용하기에는 어려움이 있습니다. 현실에서 우리가 문제를 풀 때에 상태변확확률 따위를 모두 알고있기는 힘들기 때문입니다. 이와 관련해서는 다음 포스팅에서 더 자세히 소개하겠습니다.

할인율

에이전트는 항상 현재에 판단을 내리기 때문에 현재에 가까운 보상일수록 더 큰 가치를 가지게 정의해야 합니다. '할인율' 개념을 도입해서 우리는 이를 수학적으로 표현합니다.

할인율은 γ로 표기하며, 0과 1사이의 값입니다. 시간 t로부터 k 시간이 지난 후에 보상 Rt+k을 받는다고 하면, 해당 보상은 γk-1만큼 할인됩니다. 할인율을 고려한 미래 보상의 현재 가치에 대한 수식은 다음과 같습니다.

γk-1Rt+k

0과 1사이의 값 γ를 k-1번 곱해줌에 따라 t+k 시점의 보상이 할인됩니다. k값이 커질 수록, (현재 시점으로부터 시간이 많이 지난 보상일수록) 보상의 값은 할인율 γ에 따라 줄어들게 됩니다.

정책

정책은 모든 상태에서 에이전트가 할 행동을 말합니다. 정책은 π로 표기합니다. 정책을 수식으로 나타내면 다음과 같습니다.

π(a|s) = P [ At = a | St = s ]
(시간 t에 에이전트가 상태 s에 있을 때 가능한 모든 행동 중에 a를 할 확률)

정책은 각 상태마다 어떤 행동을 할지 알려주며, 에이전트는 학습해 나가며 수많은 정책 중에서 최적 정책을 학습합니다. 최적 정책은 하나의 상태s 에서 하나의 행동a 만을 선택합니다.

가치함수

에이전트는 특정한 상태에서 앞으로 받을 보상들을 고려해서 선택을 할 수 있습니다. 현재 시점에서 앞으로 받을 보상들의 합을 계산하는 개념이 바로 가치함수입니다.

상태 가치함수

현재 시점에서 앞으로 받을 보상들의 합을 계산해 봅시다. 단순히 보상들을 더하면 다음과 같을 것입니다.

Rt+1 + Rt+2 + Rt+3 + Rt+4 + Rt+5 + Rt+6 + ...

그런데 MDP에서 우리는 할인율이라는 개념을 배웠습니다. 현재시점과 미래시점의 보상은 다르기 때문에, 보상을 받는 시점이 현재로부터 얼마나 먼가에 따라서 우리는 할인율 γk-1를 곱해줘야 합니다. 할인율을 고려한 미래 보상의 현재 가치는 다음과 같습니다. 또한 이를 반환값이라고 하며, G로 표기합니다.

Gt = Rt+1 + γRt+2 + γ2Rt+3 + γ3Rt+4 + γ4Rt+5 + γ5Rt+6 + ...

반환값이라는 것은 에이전트가 실제로 환경을 탐험하며 받은 보상들의 합입니다. 즉, 확률값이 아닌 실제의 값입니다. 에이전트는 행동을 하고 환경으로부터 보상을 받는, 그 상호작용을 반복해서 하고 마지막 상태가 됩니다. 마지막 상태가 되면 그 때 반환값을 계산할 수 있게 됩니다. 이 때 이렇게 유한한 에이전트와 환경의 상호작용을 에피소드라고 부릅니다.

그리드월드 예제에서는 처음 (1,1) 상태에서 시작하여 파란색 동그라미에 다다라 보상 1.0을 받으면 게임이 끝나므로 그 게임이 끝날 때 까지의 과정을 에피소드라고 할 수 있는 것입니다. 그리고 에이전트가 에피소드가 끝난 후에 얼마의 보상을 받았는지 계산하는 것이 바로 반환값 Gt = Rt+1 + γRt+2 + γ2Rt+3 + γ3Rt+4 + γ4Rt+5 + γ5Rt+6 + ... 입니다.

반환값으로 우리는 "각 상태의 가치"를 알 수 있습니다. 특정 상태에서의 반환값, 즉 특정 상태부터 미래 보상들의 합을 현재 가치로 계산한 반환값은 그 상태의 '가치'라고도 할 수 있을 것입니다. 그러나 반환값은 앞서 말씀드렸듯 확률값이 아닌 실제값입니다. 그러나 특정 상태의 반환값은 매 에피소드마다 다를 수 있으므로, 우리는 반환값에 대한 기댓값(평균)으로 특정 상태의 가치를 판단할 수 있습니다. 이를 상태가치함수하며 v(s)로 표기 합니다.

v(s) = E [ Gt | St = s ]

t시점에서의 상태가 s일 때, 앞으로 받을 보상들의 합인 반환값의 기댓값이 바로 상태 s의 가치를 나타내는 가치함수식입니다. Gt = Rt+1 + γRt+2 + γ2Rt+3 + γ3Rt+4 + ... 이므로, 대입하면 아래와 같이 변형할 수 있습니다.

v(s) = E [ Rt+1 + γRt+2 + γ2Rt+3 + γ3Rt+4 + ... | St = s ]

γ로 미래 시점의 보상 R들을 묶어주면 다음과 같이 변형할 수 있습니다.

v(s) = E [ Rt+1 + γ(Rt+2 + γRt+3 + γ2Rt+4 + ...) | St = s ]

Rt+2 + γRt+3 + γ2Rt+4 + ... 는 t+1시점의 반환값입니다. 따라서 아래와 같이 변형할 수 있습니다.

v(s) = E [ Rt+1 + γGt+1 | St = s ]

그런데 사실 이를 반환값 Gt+1으로 표현하기는 했지만, 사실 에이전트가 실제로 받은 보상이 아닙니다. 즉, 반환값은 실제값인데, 수식에서 뜻하고 있는 것은 앞으로 받을 것이라 예상하는 보상이며 기댓값입니다. 따라서 앞으로 받을 보상에 대한 기댓값인 가치함수로 표현하는게 보다 적절합니다. 반환값에 기댓값을 씌워 가치함수로 변형하면 다음과 같은 수식이 완성됩니다.

v(s) = E [ Rt+1 + γv(St+1) | St = s ]

그런데 에이전트가 앞으로 받을 보상에 대해 생각할 때는 늘 "정책"을 고려해주고 정책에 따라서 기댓값을 계산해주어야 합니다. 따라서 이 정책 π를 표기하면 더욱 완벽한 수식이 됩니다.

vπ(s) = Eπ [ Rt+1 + γvπ(St+1) | St = s ]

이 식은 현재 상태의 가치함수 v(s)와 다음 상태의 가치함수 v(St+1)의 관계를 방정식으로써 표현하고 있습니다. 이를 벨만 기대 방정식이라고 하며, 이 벨만 방정식을 어떻게 풀어가느냐의 문제가 바로 강화학습의 과제입니다.

행동 가치함수(큐함수)

앞서 설명한 상태가치함수는 해당 상태의 가치를 앞으로 받을 보상들의 합인 반환값의 기댓값으로 '상태의 가치'를 표현한 함수였습니다. 행동가치함수는 각 행동에 대한 가치를 알려주는 함수입니다. 이는 어떤 상태에서 어떤 행동이 얼마나 좋은지 알려주는 값입니다. 행동가치함수는 큐함수라고하며, 상태, 행동이라는 두 가지 변수를 가지며 qπ(s,a)로 나타냅니다. 큐함수를 상태 가치함수와 같이 수식으로 나타내면 다음과 같습니다.

qπ(s,a) = Eπ [ Rt+1 + γqπ(St+1, At+1) | St = s, At = a ]

상태 가치함수식과 다른 점은 수식에 변수로서 행동 A가 들어간다는 점이며, 현재 상태의 큐함수 qπ(s,a)와 다음 상태의 가치함수 qπ(St+1, At+1)의 관계는 상태 가치함수식과 같습니다. 이를 q함수의 벨만 기대방정식이라고 합니다.

그렇다면 큐함수와 상태 가치함수의 관계를 알아봅시다. 행동 가치함수(큐함수)는 어떠한 상태에서 어떠한 행동을 하는 것의 가치를 알려주는 함수이고, 상태 가치함수는 해당 상태의 가치를 알려주는 함수입니다. 따라서 가치함수와 큐함수 사이에는 관계식이 존재합니다.

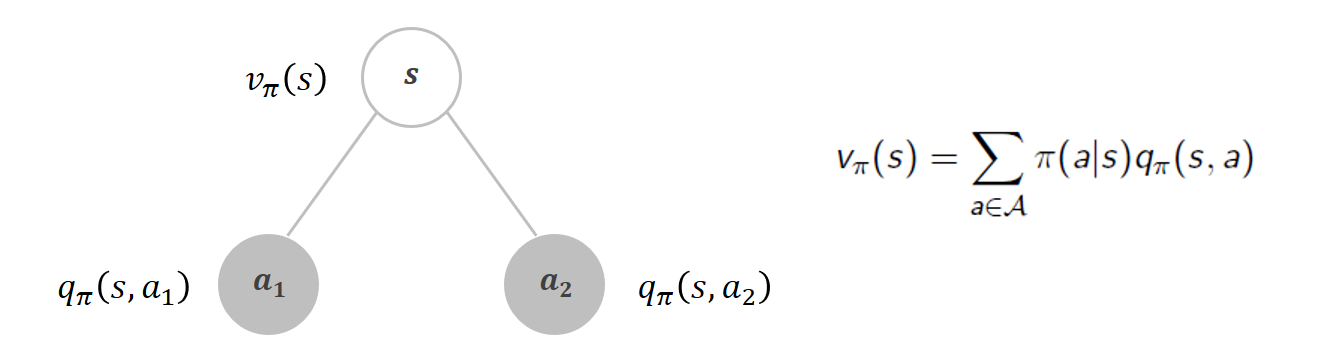
가치함수와 큐함수의 관계는 위와 같습니다. 상태 s에서 a1과 a2 두 가지 행동이 가능하다고 했을 때, a1 행동을 하는 것의 가치인 qπ(s, a1)과 a2 행동을 하는 것의 가치인 qπ(s, a2)의 합이 바로 상태가치함수 vπ(s) 입니다. 그런데 이 때, qπ(s, a)에는 해당 행동을 할 확률을 곱해주어야 합니다. 즉, vπ(s)가 해당 상태에서 가능한 행동들의 행동가치함수의 합이라고 할 때, a1, a2에 각각 a1을 택할 확률과 a2를 택할 확률을 곱해준다면 올바른 수식이 될 것입니다. 이를 수식으로 표현하면 오른쪽과 같습니다.

이 때 qπ(s, a) 앞에 곱해주고 있는 π(a|s)는 앞서 MDP의 구성요소에서 언급한 정책의 값입니다.

π(a|s) = P [ At = a | St = s ]
(시간 t에 에이전트가 상태 s에 있을 때 가능한 모든 행동 중에 a를 할 확률)

즉, 상태에서의 가능한 각 행동의 가치에 그 상태에서 그 행동을 할 확률을 곱해준 값을 모두 더해주게 되면 상태 가치가 되는 것입니다.

벨만 방정식

벨만 기대 방정식

vπ(s) = Eπ [ Rt+1 + γvπ(St+1) | St = s ]

앞서 상태가치함수를 설명할 때, 정책을 고려한 상태가치함수의 표현인 이 식은 현재 상태의 가치함수 v(s)와 다음 상태의 가치함수 v(St+1)의 관계를 방정식으로써 표현하고 있으며, 이를 벨만 방정식이라고 한다고 이야기 했습니다. 또한 이 벨만 방정식을 어떻게 풀어가느냐의 문제가 바로 강화학습의 과제 라고 이야기 했습니다. 벨만 방정식을 풀기 위해서는 위 수식을 계산 가능한 형태로 변형해야 할 것입니다. 컴퓨터(에이전트)가 계산 가능한 형태로 위 벨만 방정식이 의미하는 바를 변형해 봅시다.

최우선 과제는 기댓값을 어떻게 계산할지를 변형하는 것입니다. 기댓값에는 큐함수와 상태가치함수 사이의 관계를 표현할 때 곱해주었던 "어떠한 행동을 할 확률"(정책값 π(a|s))과 그 행동을 했을 때 어떤 상태 s'로 가게 되는 확률(상태변환확률 Pass') 둘을 고려해야 합니다. 이 둘을 고려한 계산 가능한 벨만 방정식의 형태는 다음과 같습니다.

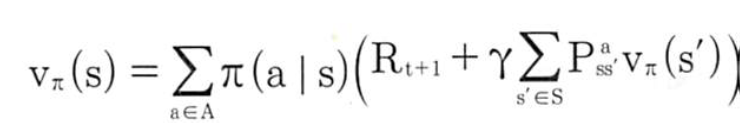
즉, 각 행동에 대해 그 행동을 할 확률을 고려해주고(π(a|s)), 각 행동을 했을 때 받을 보상과(Rt+1) γ로 할인된 다음 상태의 가치함수와 상태 변환 확률의 곱을 고려하는 것입니다.

벨만 최적 방정식

최적 정책이란 모든 정책에 대해 가장 큰 가치함수를 주는 정책입니다. 최적의 가치함수와 최적의 큐함수는 다음과 같이 수식으로 표현할 수 있습니다.

최적의 가치함수 : v*(s) = max[vπ(s)]

최적의 큐함수 : q*(s,a) = max[qπ(s,a)]

현재 상태의 가치함수가 최적이라고 가정해봅시다. 현재 상태의 가치함수가 최적이라는 것은 에이전트가 가장 좋은 행동을 선택한다는 것이고, 따라서 최적의 큐함수 중에 max를 취하는 것이 최적의 가치함수가 됩니다. 따라서 최적 가치함수 v*(s)는 다음과 같습니다.

max[q*(s,a) | St = s, At = a]

큐함수를 가치함수로 고쳐봅시다. 이를 벨만 최적 방정식이라고 부릅니다.

maxE[Rt+1 + γv*(St+1) | St = s, At = a]

큐함수에 해서도 벨만 최적 방정식을 표현할 수 있습니다. 최적 정책을 따라가고 있을 때 현재의 큐함수는 다음 상태에서 선택 가능한 행동 중에서 가장 높은 값의 큐함수를 한번 할인하고 보상을 더한 값과 같을 것입니다. q*(s,a)는 다음과 같습니다.

E[Rt+1 + γmaxq*(St+1,a') | St = s, At = a]

여기서 a'는 바로 다음 상태에서 선택 가능한 행동 중 가장 가치가 높은 행동을 의미합니다. 이 벨만 기대 방정식과 벨만 최적 방정식으로 순차적 의사결정 문제를 풀어낼 수 있는데, 이 문제를 모델에 대해 알고 있다는 가정하에 '계산'해 내어 푸는 방법이 바로 다이나믹 프로그래밍입니다. 다이나믹 프로그래밍에 대해서는 다음 포스팅에서 다루겠습니다.

다음 포스팅

다음 포스팅에서는 다이나믹 프로그래밍과 그 한계에 대해 포스팅합니다.