Section 5_Sprint 3

JIYOUNG KIM·2022년 4월 11일

section5 코드스테이츠

Codestates AIB

목록 보기

15/15

Day 1

Hash Table

해시테이블 관련 용어

해시테이블
- 해시함수를 사용해서 특정 해시값을 알아내고(→ 검색) 그 해시값을 인덱스로 변환하여 키값과 데이터를 저장하는 자료구조
- 해시함수
  - 데이터를 효율적으로 관리하기 위한 목적으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수
  - 해시함수의 계산으로 산출된 값을 해시값이라 함
  - 입력값이 같다면 동일한 출력값을 받아야 함
- 탐색, 삽입, 삭제 속도가 빠름 → O(1)
- 파이썬에서는 딕셔너리 로 구현
해싱 : 해시함수를 사용해서 인덱스를 구성하는 과정
- 데이터 → 해시함수에 의해 분류 → 분류된 데이터 해시테이블 안에 들어가는 과정
- (장점) 데이터 양에 영향을 덜 받고 성능이 빠름(← 키를 통해 값을 검색)
- 이중해싱과 해시의 해시의 차이

해시탐색법의 특징

해시탐색 : 데이터의 내용과 저장한 곳의 요소를 미리 연결해 둠으로써 극히 짧은 시간안에 탐색할 수 있도록 고안된 알고리즘
- 효율적으로 배열을 사용하기 위해 데이터에 일정한 계산을 실시해 결과값과 같은 인덱스를 가진 요소에 보관하는 방법
- 나중에 데이터를 탐색하기 쉽도록 데이터를 보관하는 단계에서 사전준비를 해두는 것
- Linear probing, Quadratic probing, Double hashing
  - https://ict-nroo.tistory.com/76
  - https://velog.io/@jaeyunn_15/DataStructure-%ED%95%B4%EC%8B%9C-%EC%B6%A9%EB%8F%8C%EA%B3%BC-%ED%95%B4%EA%B2%B0-%EB%B0%A9%EB%B2%95 (이중해시)

해시테이블 성능

탐색, 삽입, 삭제 → 평균 O(1)
- 상수시간 : 해시테이블의 크기에 상관없이 항상 똑같은 시간이 걸림
단점
- 순서가 있는 배열에는 어울리지 않음
  - 순서와 상관없이 키를 통해 해시를 찾아 저장하기 때문
- 공간 효율성이 떨어짐
  - 데이터가 저장되기 전에 미리 저장공간 확보해 놓아야 함
- 해시함수의 의존도 높음

해시 충돌

키가 들어갈 자리가 없는 경우에 발생
대처방법
- 체이닝 : 해당 인덱스에 이미 값이 있으면 그 뒤에 체인으로 연결
  
  (장점)
  - 한정된 저장소를 효율적으로 사용 가능 → 상대적으로 적은 메모리 사용
  - 메모리 공간을 미리 잡아 놓을 필요가 없음
  (단점)
  - 한 해시에 자료들이 계속 연결된다면 (= 쏠림현상) 검색 효율 ↓
  - 외부 저장공간을 사용하고, 여기에서 추가로 작업을 해야함
- 오픈어드레싱 : 리니어 프로빙(선형탐사)
  - 탐사를 진행하면서 빈 공간을 찾아 해결
    - 체이닝과 달리 저장공간 정해져있음
    - 파이썬의 경우 내부적으로 오픈어드레싱 방식 활용
    - 빈 공간이 없는 경우 시간 오래걸림 → 로드팩터를 작게 설정해 성능 저하 문제 해결
  - (질문) 충돌시 테이블 리사이징하는데 그때 값을 재계산해서 데이터를 넣어주는지 → 재계산해서 리사이징
    - https://courses.csail.mit.edu/6.006/spring11/rec/rec07.pdf
    - 해시테이블 크기 조정은 새 크기에 매핑할 새 해시함수를 선택하고 새 크기의 해시테이블을 만들고, 이전 테이블의 요소를 반복하고 새 테이블에 삽입하는 작업으로 구성
  (장점)
  - 또 다른 저장공간 없이 해시테이블 내에서 데이터 저장 및 처리 가능 → 또 다른 저장공간에서의 추가작업 X
  (단점)
  - 해시함수의 성능에 전체 해시테이블의 성능의 좌지우지됨
  - 데이터의 길이가 늘어나면 그에 해당하는 저장소 마련 필요(테이블 리사이징)

로드팩터 = 적재율

적재율 : $\frac {실제 사용하는 키 개수} {테이블의 크기}$
로드팩터를 수치로해서 테이블 리사이징을 자동적으로 해주는 형태
더 낮은 로드팩터 = 더 적은 충돌가능성 = 고성능
오픈어드레싱을 사용하면 최대 로드팩터는 1
체이닝을 사용하면 로드팩터(<= 1)는 오픈어드레싱보다 좋은 성능을 보임

Day 2

Graph

개념

그래프는 vert(노드, 정점)와 edge(간선) 으로 연결된 자료구조로 object간의 관계 표현에 유용
그래프와 트리의 차이점
- 정의
  - 그래프 : 노드와 그 노드를 연결하는 간선을 하나로 모아놓은 자료 구조
  - 트리 : 그래프의 한 종류인 DAG의 한 종류
- 방향성
  - 그래프 : 방향그래프, 무방향 그래프 모두 존재
  - 트리 : 방향그래프
- 루트노드
  - 그래프 : 루트노드의 개념 없음
  - 트리 : 한 개의 루트노드만 존재
- 부모-자식
  - 그래프 : 없음
  - 트리 : 부모-자식 관계 존재
- 그래프는 노드간의 관계, 트리는 노드간의 계층을 표현
directed edge(방향성 간선) : 그래프가 한쪽 방향(one-way)으로 설명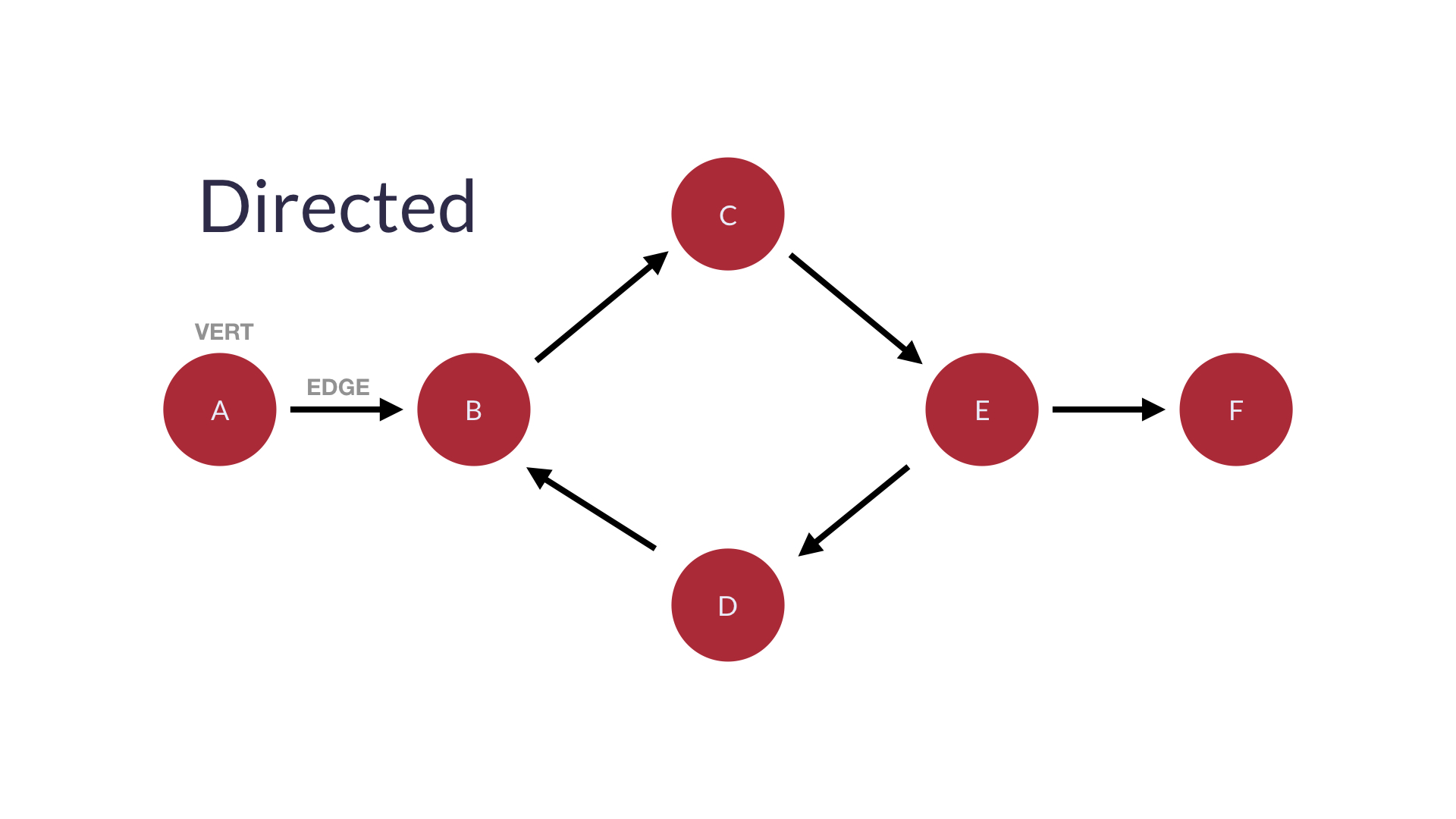
- bidirectional edge(양방향 간선)
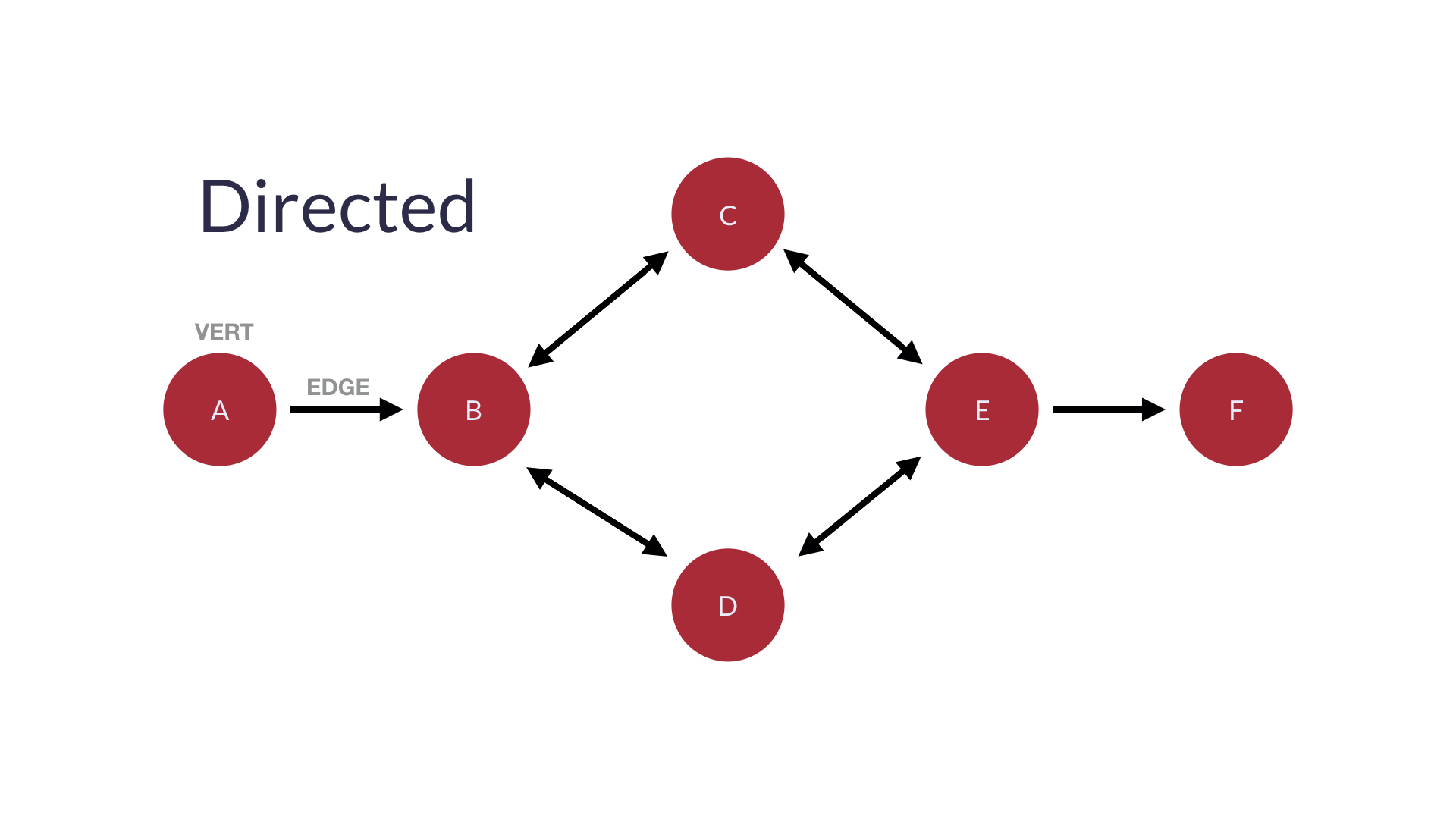
undirected edge(무방향성 간선) : 방향이 따로 지정되어 있지 않음, 서로 상호교환함
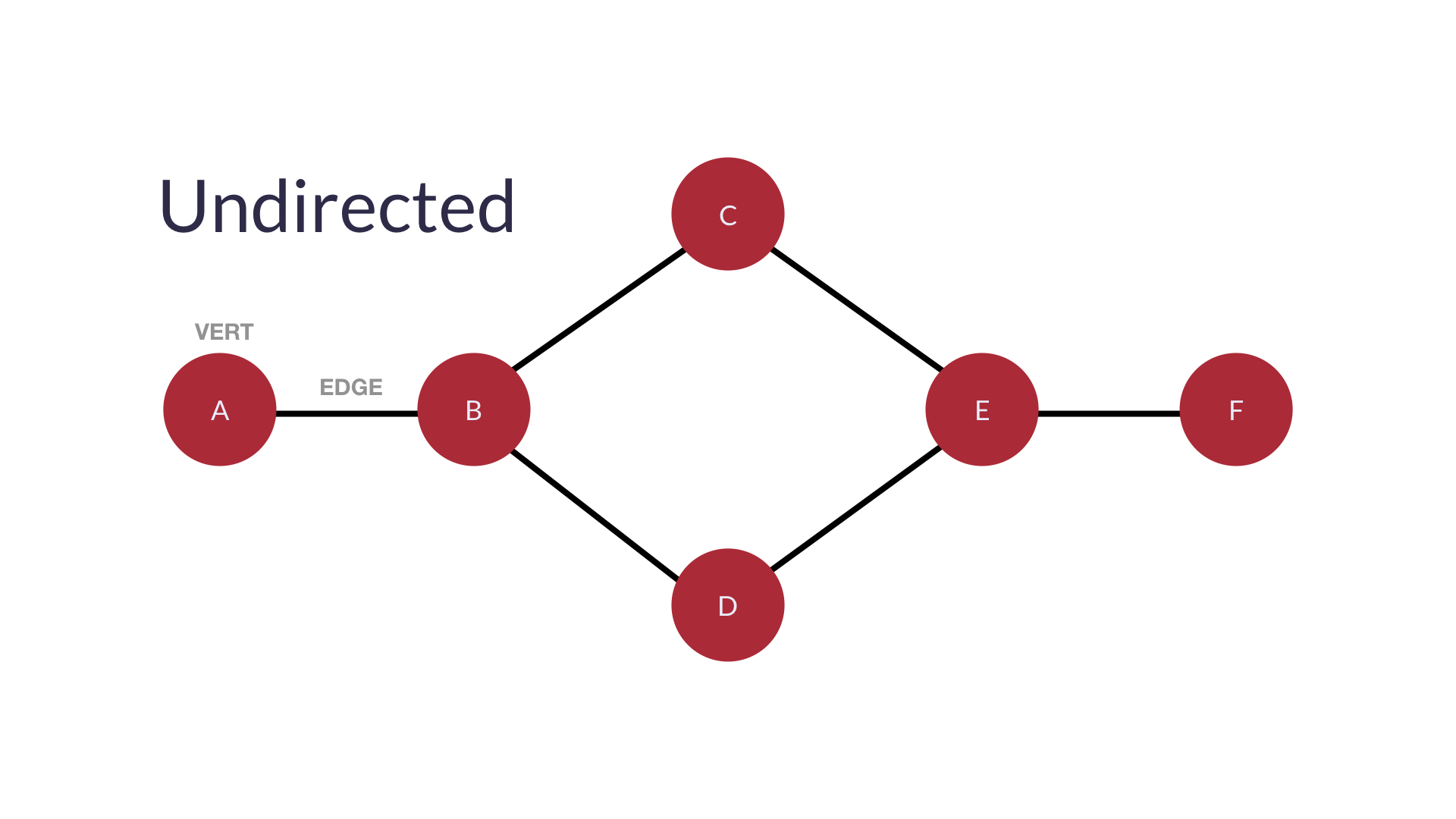
- 상호교환 : 화살표로 연결된 노드들이 서로 노드정보를 공유하는 것
인접(adjacent)
- 무방향성 그래프에서 정점 u,v에 대하여 간선(u,v)이 있으면 정점 u는 정점 v에 인접하다고 함(역도 성립)
- 방향성 그래프에서 정점 u,v에 대하여 간선(u,v)이 있으면 정점 v는 정점 u에 인접하다고 함(역은 성립하지 않음)
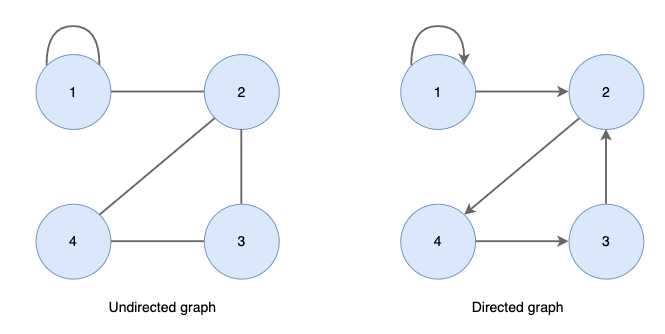
  - 두 그래프 다 정점 2는 정점 1에 인접
  - 무방향성 그래프에서 정점 1은 정점 2에 인접하나 방향성 그래프는 아님
부속(incident)
- 무방향 그래프에서 정점 u,v에 대하여 간선(u,v)이 있으면 간선(u,v)은 정점 u와 v에 부족한다 함

그래프의 유형

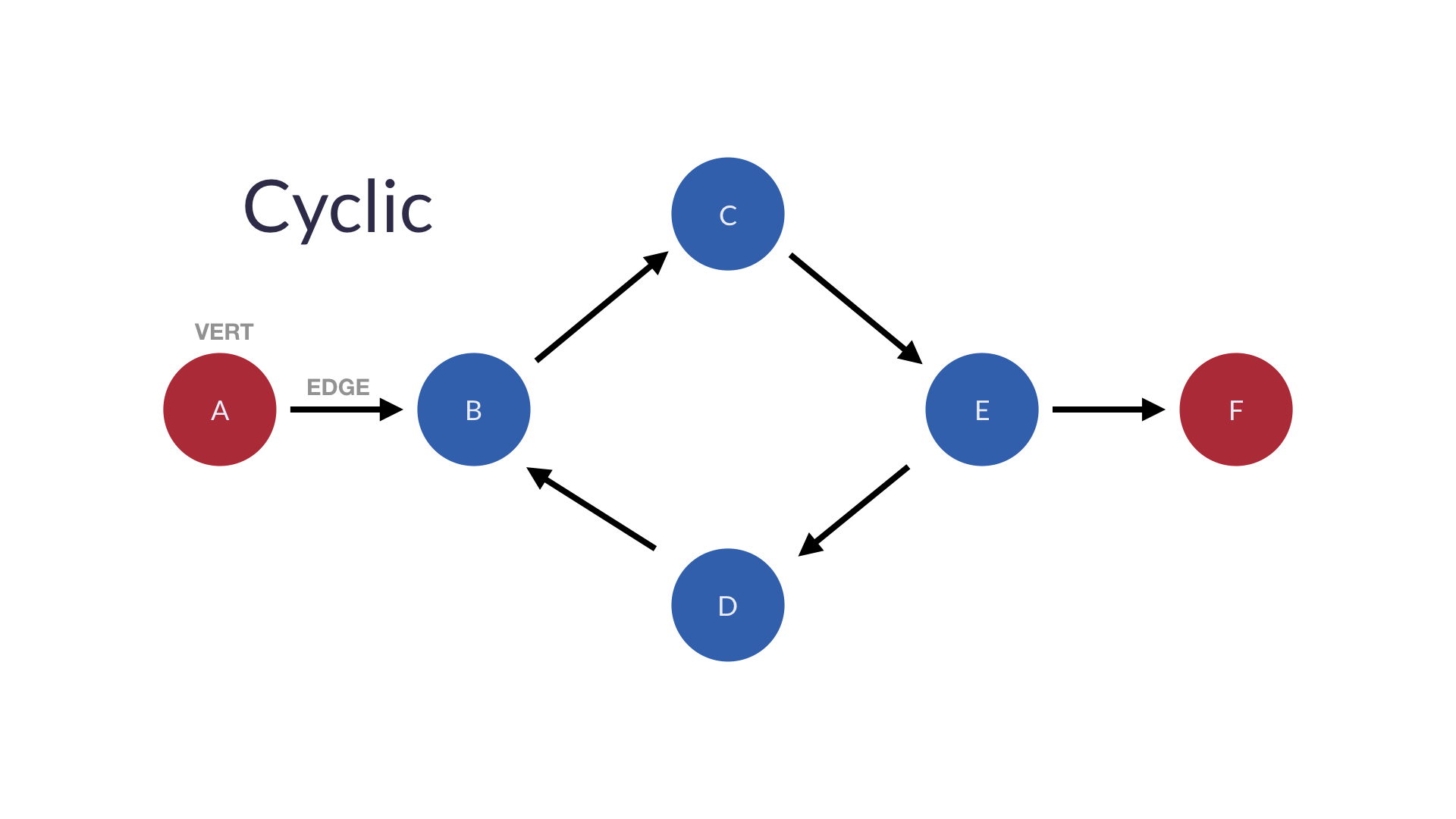
Cyclic graphs(순환 그래프) : 순환(루프)를 형성할 수 있는 경우
- 방문한 노드에 다시 방문
- undirected 그래프
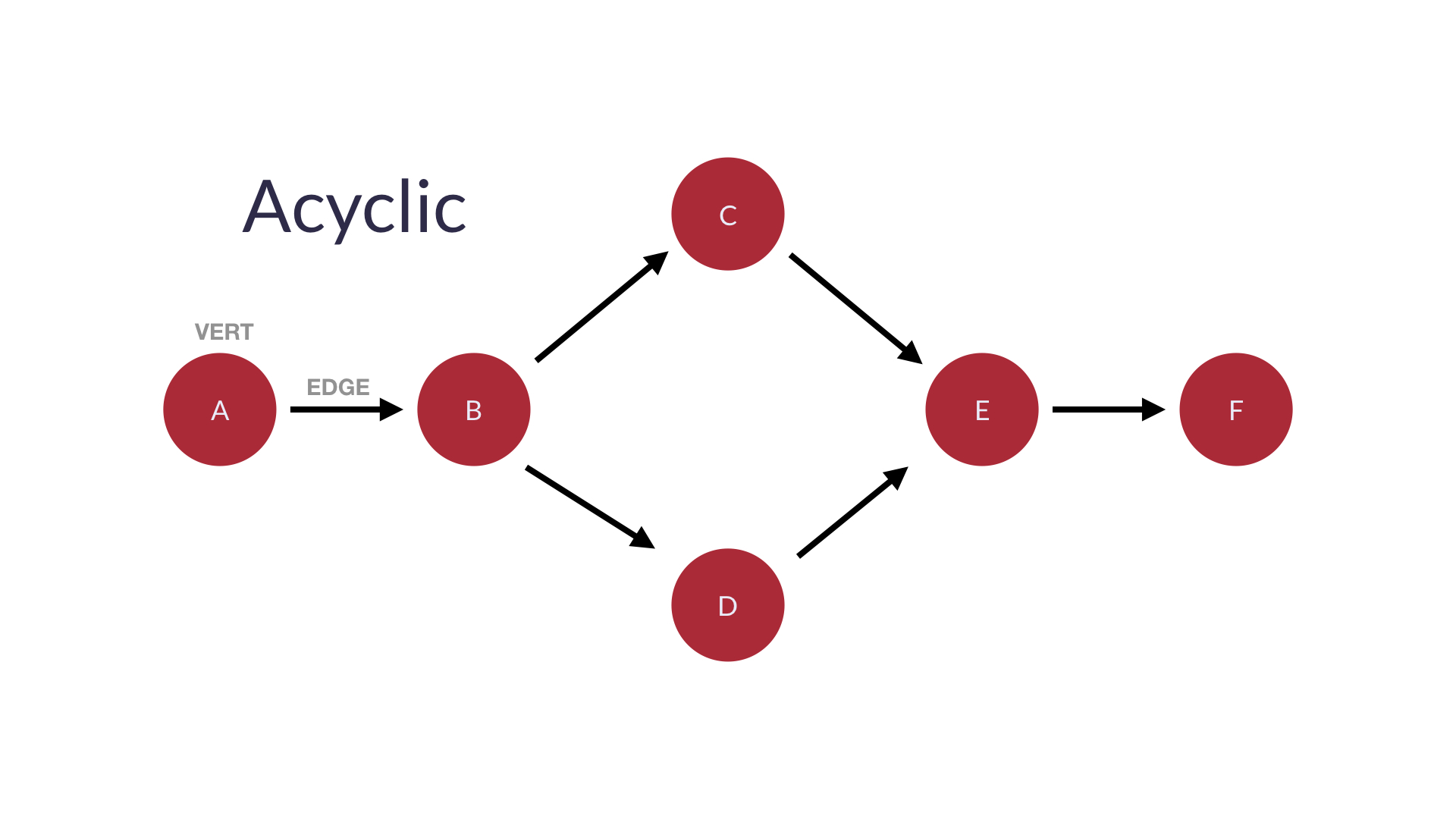
Acyclic graphs(비순환 그래프)
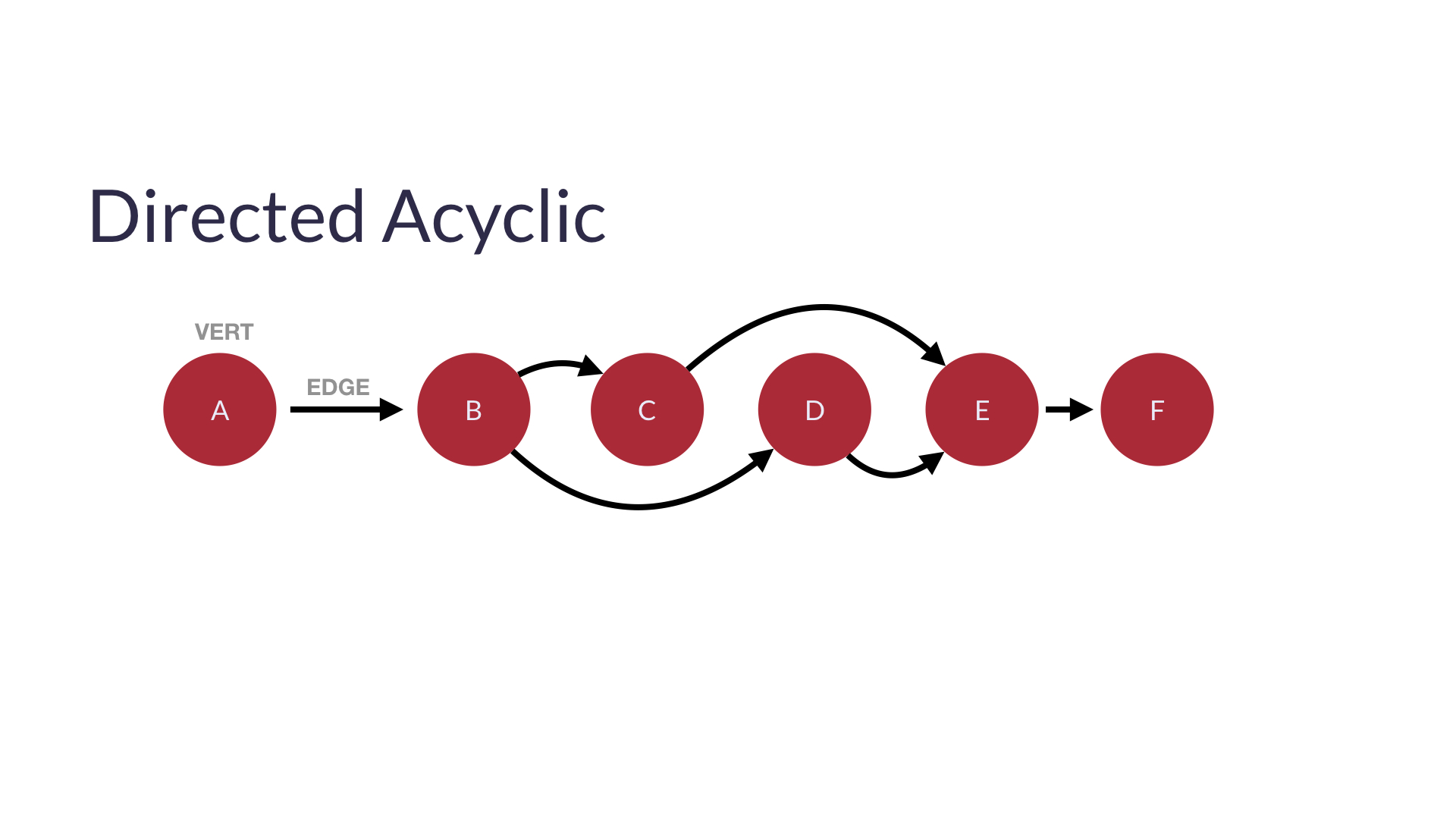
Directed acyclic graphs(DAGs, 방향성 비순환그래프)
- 순환되지 않고 특정한 단방향 그래프
- 선형(단방향)으로 정렬 가능
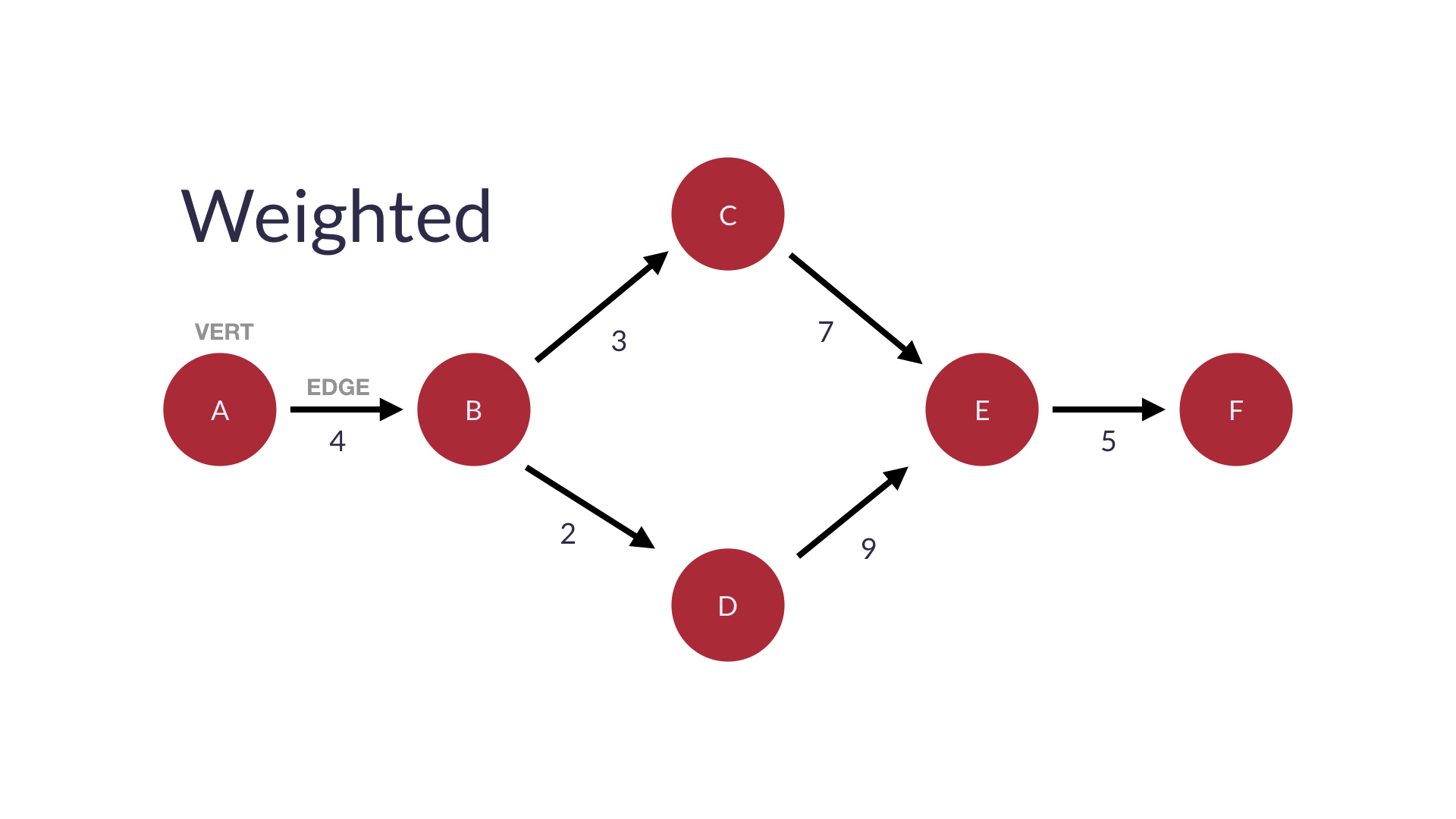
Weighted graphs(가중 그래프)
- 각 edge의 가중치에 할당된 특정값을 호출
- 가중치는 서로 다른 그래프에서 서로 다른 데이터를 나타냄
- 경로의 총 가중치가 높을 수록 경로이동시간(비용)이 길어짐

그래프를 나타내는 방법

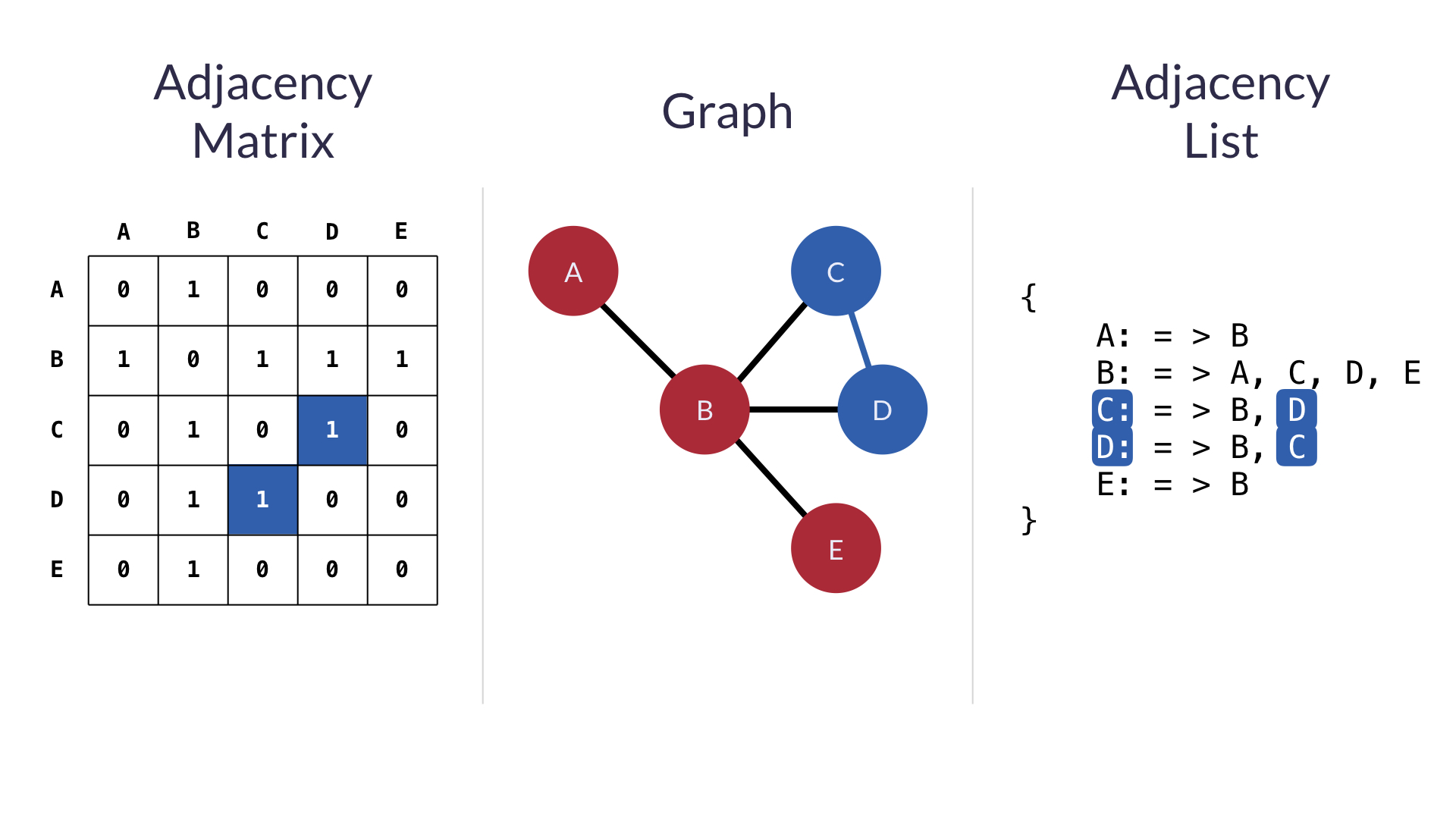
인접리스트(adjacency lists)

전체 노드 목록을 저장

class Graph:
    def __init__(self):
        self.vertices = {
                         "A": {"B"},   # 여기서 {"B"}가 set의 형태이다.
                         "B": {"C", "D"}, # {"B" : {}}의 형태는 딕셔너리
                         "C": {"E"},     # 즉, 딕셔너리 안에 set이 있는 것이다.
                         "D": {"F", "G"},
                         "E": {"C"},
                         "F": {"C"},
                         "G": {"A", "F"}
                     }

vertices(정점)은 O(1) 상수시간에 각 edge에 접근 가능
(단점) 특정 노드간의 연결관계를 확인하기 위해서는 반복문이 활용되어야 함 → 시간복잡도 O(n) 이상

인접행렬(adjacency matrices)

class Graph:
    def __init__(self):
        self.edges = [[0,1,0,0,0,0,0],
                      [0,0,1,1,0,0,0],
                      [0,0,0,0,1,0,0],
                      [0,0,0,0,0,1,1],
                      [0,0,1,0,0,0,0],
                      [0,0,1,0,0,0,0],
                      [1,0,0,0,0,1,0]]

edge weights(간선가중치) 알 수 있음
0 은 관계없음을, 다른 값은 edge label 혹은 edge weight를 나타냄
(장점) 구현이 쉬움
(단점)
- 노드 값과 해당 인덱스 사이에 연관성 없음
- 특정 노드에 방문한 노드들을 알기 위해서는 모든 노드 확인해야 함 → 시간복잡도 O(n)

인접리스트와 인접행렬 모두 구현 → vertex 및 edge클래스를 포함하여 더 많은 정보 파악 가능
시간복잡도
- 노드개수가 n이고 edge 개수가 m일 때,
- 메모리에서
  - 인접리스트 O(n+m)
  - 인접행렬 O(n^2)
- u와 v라는 edge가 존재하는 지
  - 인접리스트 : graph[u].search(v) → 최악 O(n)
    - 각 노드가 가질 수 있는 최대 edge의 개수가 n 이기 때문
  - 인접행렬 : if graph[u][v] == 1 → O(1)
- u에 인접한 모든 노드 v에 대해 특정 액션을 취해라
  - 인접리스트 : for each edge in graph[u] → O(인접한 노드 수)
  - 인접행렬 : for v in range(1, n+1) → O(n)
- 새로운 엣지(u,v) 삽입
  - 인접리스트 : O(1)
  - 인접행렬 : graph[u][v] = 1 or 가중치 → O(1)
- 기존 엣지 삭제
  - 인접리스트 : graph[u].search[v] → remove → 최악 O(n)
  - 인접행렬 : graph[u][v] = 0 → O(1)

순회(traversal)

그래프 또는 트리처럼 연결된 구조에서 노드를 한번씩 탐색하는 개념
방향에 따라 탐색방법 달라짐
아직 방문하지 않은 노드의 순회 순서 중요
탐색 알고리즘 : DFS, BFS → Day 3
트리의 순회
- 전위순회(preorder traverse) : 루트 노드 → 왼쪽 노드 → 오른쪽 노드
- 중위순회(indorder traverse) : 왼쪽 노드 → 루트 노드 → 오른쪽 노드
- 후위순회(postorder traverse) : 왼쪽 노드 → 오른쪽 노드 → 루트 노트

Day 3

BFS와 DFS

순회(방문)하면서 탐색하는 탐색 알고리즘, 그래프 탐색 알고리즘
→ 출발지 노드와 그래프/트리 구조에 따라 탐색하는 순서와 노드가 달라질 수 있음

(목적) 모든 또는 특정 정점을 1번씩 방문하기 위한 것
두 방법 모두 각각의 노드에 방문했는지 안했는지 체크하는 배열 필요

개념

BFS(Breadth First Search, 너비 우선 탐색)
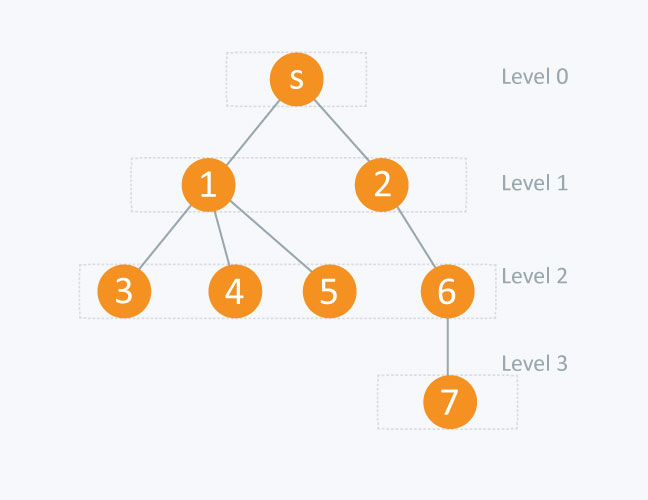
- 루트 노드에서부터 시작해서 인접한 노드를 먼저 탐색하는 방법
- 큐 개념 사용(FIFO)
  - 재귀호출은 사용하지 않음 → 인접한 노드에 대해 먼저 탐색하기 때문
- S → 1 → 2 → 3 → 4 → 5 → 6 → 7
- 노드가 적은 경우 최단경로 탐색할 때 유용
- 노드가 많아지는 경우 메모리 저장공간이 증가
- 장점
  - 너비를 우선으로 탐색하기 때문에 답이 되는 경로가 여러 개인 경우에도 최단 경로임을 보장
  - 최단경로가 존재한다면 어느 한 경로가 무한히 깊어진다 해도 최단 경로를 반드시 찾을 수 있음
  - 노드 수가 적고 깊이가 얕은 해가 존재할 때 유리
- 단점
  - 재귀호출을 사용하는 DFS와 달리 큐를 이용해 다음에 탐색할 노드들을 저장하기 때문에 노드의 수가 많을 수록 필요없는 노드들까지 저장해야 하기 때문에 더 큰 저장공간 필요
  - 노드의 수가 늘어나면 탐색해야 하는 노드가 많아지기 때문에 비효율적
DFS(Depth First Search, 깊이 우선 탐색)
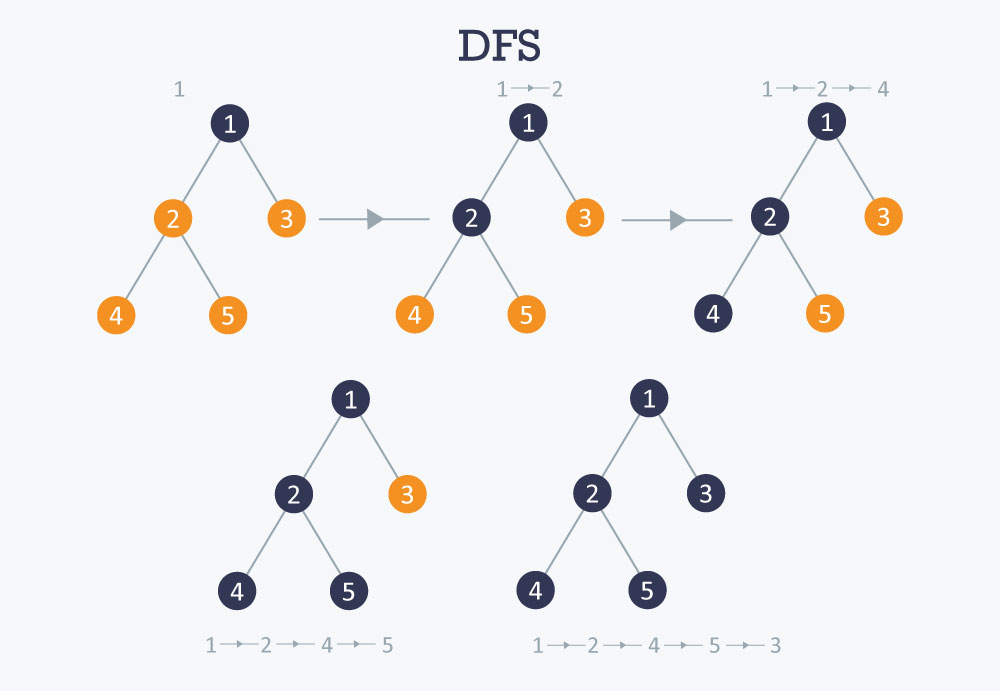
- 마지막 노드까지 방문한 다음 역추적해서 방문하지 않은 노드를 방문
- 스택 개념 사용(LIFO), 재귀함수 사용
- 1 → 2 → 4 → 5 → 3
- 다른 경로를 역추적(backtracking)하고 탐색하기 전에 가능한 그래프를 분할
- 재귀적으로 아래에서부터 탐색하지 않은 정점이 있는지 확인
- 모든 노드를 방문하는 경우 사용
  - 최단 경로를 찾지 못하고 시간이 오래 걸릴 수 있음
- 경로의 특징을 저장해두어야 하는 문제인 경우 사용
- 장점
  - BFS에 비해 저장공간의 필요성이 적음 → backtracking을 해야하는 노드들만 저장해주면 됨
  - 찾아야하는 노드가 깊은 단계에 있을 수록 그 노드가 좌측에 있을 수록 BFS 보다 유리
- 단점
  - 답이 아닌 경로가 매우 깊다면 그 경로에 깊이 빠질 우려가 있음 → 무한반복 에러가 발생할 확률이 높아짐
  - 찾은 해가 최단 경로라는 보장 없음

소스코드

# 시작 정점을 방문
# 시작 정점에 인접한 모든 정점들을 우선 방문
# 더 이상 방문할 정점 없으면 한 depth내려가서
# 다시 인접한 모든 정점들 우선 반복

(처음) 시작 정점을 큐에 삽입하고 방문처리한다.
1) 큐에서 하나의 노드를 꺼냄
2) 꺼낸 노드와 인접한 노드 중에 방문하지 않은 노드를 큐에 삽입하고 방문처리한다.
1, 2과정을 큐가 비어있을 때까지 반복한다.

# 스택
# 시작 정점을 방문한 후
# 자식을 모두 탐색
# 이때 연결된 노드가 존재하지 않을 때가지 들어왔다면
# 한 단계 이전으로 돌아가 다시 알고리즘 수행

(처음) 탐색을 시작할 때 첫번째 노드를 스택에 삽입
1) 스택에 삽입된 최상단 노드 주변에 방문하지 않았던 인접노드(가장 작은 번호 먼저)가 있으면 해당 노드를 스택에 삽입하고 방문처리한다.
    → 방문처리 : 스택에 삽입되었던 노드가 중복적으로 또 삽입되지 않기 위함
2) 최상단 노드에 인접한 노드가 없으면 스택에 최상단 노드를 꺼낸다(pop)
1,2 과정을 스택이 빌 때까지 반복한다.

# 재귀
base condition : 파라미터로 넘어온 노드가 이미 방문한 노드라면 return
파라미터로 넘어온 노드가 방문하지 않은 노드라면 방문표시를 하고 인접한 노드에 대해 재귀적으로 함수를 호출하며 탐색을 진행

Day 4

Algorithm Advanced

Dynamic Programming(동적 계획법)

하나의 문제를 중복되는 서브문제로 나누어 푸는 방법
분할정복과 유사
- 차이점
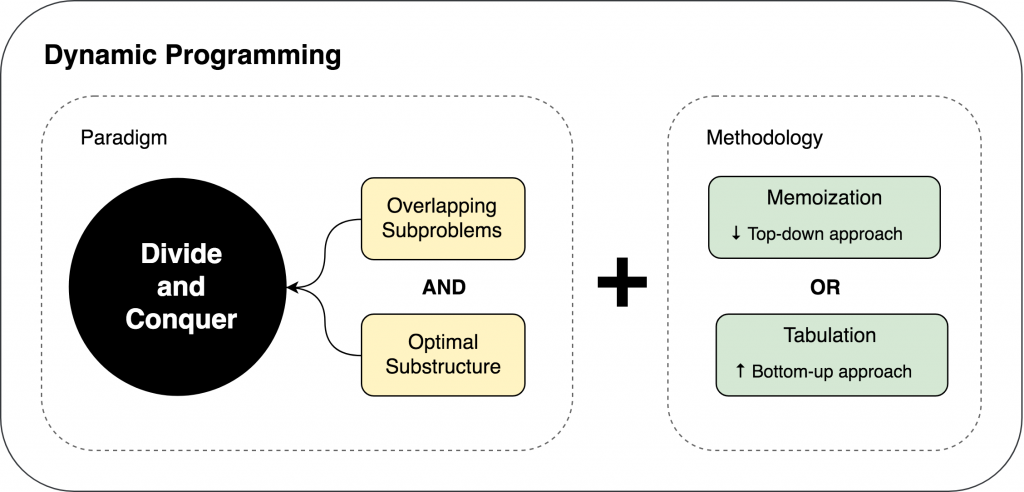
  - DP는 문제를 분할하는 경우 중복되는 서브문제가 있고, 분할정복은 서브문제가 독립적
  - DP는 서브문제가 같을 경우 메모이제이션을 활용하여 같은 문제에 대해 해결할 수 있고, 분할정복은 서브문제가 다르기 때문에 메모이제이션 활용X
  - DP를 활용하면 해결할 수 있는 문제의 범위 넓어짐
특징
- 중복(반복)되는 서브문제 → 메인과 서브문제를 같은 방법으로 해결
- 메인문제 해결방법을 서브문제에서 구하여 재사용하는 구조
  
  → 최적부분 구조로 구성된 중복되는 서브문제를 분할정복으로 해결
방법론
- Memoization(하향식방법, Top-down)
  - 메인문제를 분할하면서 해결하는 방법, 한번 계산했던 결과를 메모리 공간에 기록해 두었다가 필요할 때 가져와서 씀
  - 큰 문제에서 하위 문제로 접근해서 하위 문제에 대한 정답을 계산했는지 확인하면서 문제를 푸는 방식
  - 답을 재활용하기 때문에 중복계산을 방지할 수 있음
- Tabulation(상향식방법, Bottom-up) : 가장 작은 문제를 먼저 해결하고 최종적으로 메인문제를 해결하는 방법
  - 하위 문제의 정답을 이용해 더 큰 문제의 정답을 풀어나가는 방식
  - 아래에서부터 계산을 수행하고 누적시켜서 전체 큰 문제를 해결하는 방식
재귀 + 조건 → 분할정복 + 조건 → DP + 조건 → 방법론
동적계획법 적용할 수 있는 문제 유형
- 문제가 더 작은 문제로 쪼개질 때
- 작은 문제의 솔루션으로 더 큰 문제의 솔루션을 구할 수 있을 때
- 이 작은 문제들이 겹쳐서 이를 저장하고 사용하여 계산의 수를 많이 줄일 수 있을 때
- ex. 이진검색, 최단경로 알고리즘, 최적화 문제, 외판원 문제

탐욕 알고리즘

최적의 해 또는 근사 해를 구하는 데 사용하는 방법
발견법(heuristic method)의 방법 중 하나
- 발견법 : 최선, 최적의 답을 찾기보다 주어진 상황에서 한 단계씩 빠른 시간 내에 해결하기 위해 사용
- 역추적과 같이 알고리즘 수행시간이 많이 걸릴 때 사용(ex. 외판원 문제)
- 문제의 경우의 수가 기하급수적으로 늘어나면 고려할 수 있음
특징
- 다른 문제들과 독립적 → 다른 노드의 선택에 영향을 고려하지 않음
- 탐욕 알고리즘의 결과가 최적의 해는 아닐 수 있음 → 순간최적을 위한 답을 찾 방법
- 구현이 간단하면서 보통 정답에 가까운 정답을 도출해 냄
  - 정확한 답, 시간을 내는 것과 트레이드 오프가 된다고 할 수 있음 → 근사 알고리즘 : 어떤 최적화 문제에 대한 해의 근사값을 구하는 알고리즘

JIYOUNG KIM

데이터분석가

이전 포스트

Section 5_Sprint 3

Codestates AIB

Day 1

Hash Table

해시테이블 관련 용어

해시탐색법의 특징

해시테이블 성능

해시 충돌

로드팩터 = 적재율

Day 2

Graph

개념

그래프의 유형

그래프를 나타내는 방법

순회(traversal)

Day 3

BFS와 DFS

개념

소스코드

Day 4

Algorithm Advanced

Dynamic Programming(동적 계획법)

탐욕 알고리즘

Section 5_Sprint 2

0개의 댓글