
Day 1
Data Structure Fundamental
ADT(Abstract Data Structure, 추상자료형)
-
추상적으로 필요한 기능을 나열한 일종의 로직
- 기본자료형(리스트, 숫자, 문자열)을 활용하여 사용자에 의해 구형
-
Linked-list : 리스트들을 연결해줌, 참조되는 노드의 위치바꾸기
- 연결은 프로그래밍에서 참조기능으로 구현
- 연결리스트는 리스트의 길이를 별도로 지정해줄 필요 없음
- 별도의 인덱스 지정할 필요없이 연결되는 구조
- 연결리스트의 각 요소는 참조하는 노드에 저장
- 각 노드는 연결리스트의 다음 노드에 대해 참조(포인터)를 함
- 참조 :
.로 지칭 - 삽입, 할당 :
=로 표현
- 참조 :
- 각 노드는 연결리스트의 다음 노드에 대해 참조(포인터)를 함
-
Stack : Last in First out, 뒤로가기 버튼, ctrl+z...
append,pop으로 stack 구현 가능
-
Queue : First in First Out, 임일 전달, 푸쉬 알랑 기능, 쇼핑몰에서 주문 처리(선착순), 전화 온 순서대로 업무 처리....
- PUSH : 데이터 넣는 것
- POP : 데이터 꺼내는 것
- dequeue(double-ended queue) : 큐에서 양방향으로 데이터를 처리
- 삭제 : 실제로 값을 빼거나 삭제시키는 개념 아님
- enqueue : 새로운 노드의 저장공간(변수)를 만들어주고 그 저장공간에 노드 넣어주는 개념
- dequeue : 삭제할 노드를 위해 저장공간(변수)를 만들어주고 그 저장공간에 삭제노드를 넣어주는 개념
Q & A
자료구조란?
- 자료를 쉽게 관리하기 위해 다양한 구조로 묶는 것
- 자료를 저장하는 방법
- data structure → 자료구조, 자료 → 데이터
- 다양한 자료구조 → 각각의 자료구조마다 장단점 有
자료구조를 사용하면 좋은점?
- 똑같은 알고리즘도 어떤 데이터 구조를 사용하는 지에 따라
효율성이 달라짐- 모든 자료구조가 같은 효율성을 지니는 것은 아님
- 배열은 배열 안에 있는 자료를 불러오는 것(Read)이 빠름
- 모든 자료구조가 같은 효율성을 지니는 것은 아님
- 연결리스트
- (단점) n번째 자료에 접근하기 위해서 1번부터 모든 데이터를 거쳐서 가야하기 때문에 Read 연산이 느림
- (장점) 데이터를 삭제, 추가하는 연산이 빠름 - 배열은 경우에 따라 느림
- 데이터를
관리하는 데 도움- 선착순 → 수강신청, 티켓팅
- 배열, 큐 자료구조
배열
- 기본적인 자료구조 배열
- 선형자료구조 → 자료를 순차적으로 나열
- 배열
- 정해진 크기의 같은 타입의 데이터를 저장하는 구조
- 동적배열
- 크기가 정해지지 않은 데이터를 저장하기 위해 고안
- 연결리스트
- 각각의 데이터가 다음 데이터를 가리키도록 해ㅓㅅ 중간에 추가나 제거가 쉽게 되도록 고안
- 배열
- 비선형자료구조 → 하나의 자료뒤에 다수의 자료가 올 수 있는 형태
연결리스트, 자료구조의 시간복잡도
- 자료구조의 시간복잡도
- 데이터 연산 4개 : Read, Search, Add, Delete
- 연결리스트
- 종류
singly linked list: 노드당 다음 노드를 알려주는 링크가 하나 뿐, 한방향으로 밖에 이동을 못함doubly linked list: 노드당 링크가 2개, 이전 노드를 갈 수 있는 링크를 추가하게 되는 것, 양방향으로 움직일 수 있음Circular(환형) linked list: 더블일 수도 있고 싱글일 수 있음, 마지막 노드가 첫번째 노드를 가르켜서 계속 회전할 수 있음
- 종류
- 배열은 데이터가 한 칸씩 다 땡겨와야 하는데 연결리스트는 중간에 끊는 거 가능함
추상화
- 핵심 개념이나 기능을 간추려 내는 것 → 개념을 만들어가는 과정
ADT
- 추상 자료형
- 세부 구현으로부터 분리해 핵심 개념이나 기능을 간추려 낸 자료형
- 스택, 큐, 덱, 리스트, 이진트리 같은 자료구조
- 프로그래밍 관점에서 추상자료형의 장점
- 반드시 필요한 기능이지만 내부 구현은 사용자에게 맡김으로서 사용의 유연함을 제공할 수 있음(다형성)
stack
- Last In First Out
- ctrl + z (undo 기능)
- 자료의 입출력이 한 방향에서만 이루어지는 자료구조
push: 스택에 데이터를 추가하는 기능pop: 스택의 최상위 데이터를 꺼내는 기능- 스택의 맨 위의 값을 가리키는 용어 :
top,
- 스택의 맨 위의 값을 가리키는 용어 :
queue
- First In First Out
- 줄서기
- 한 쪽 끝에서 데이터의 입력(삽입 연산)만 가능하고 반대쪽 끝에서는 출력(삭제 연산)만 가능한 자료구조

- 데이터를 넣는 쪽 :
rear - 데이터를 꺼내는 쪽 :
front - 큐에서 front는 맨 앞의 원소를, rear는 맨 끝의 원소를 가리킴
- enqueue : 큐에 값을 집어 넣는 함수(스택의 push 역할)
- dequeue : 큐에 값을 빼내는 함수(스택의 pop 역할)
동적배열과 연결리스트
- 두 자료구조의 차이점
- 삽입과 삭제 → 연결리스트
- 임의의 원소에 접근하는 데 드는 시간 → 동적배열
Day 2
Data structure Intermediate
검색(Searching)
- 특정 노드를 추가하거나 삭제를 위해서는 검색이 우선되어야 함
- 다양한 알고리즘을 활용하는 경우 최적 알고리즘 경로를 측정하는데 사용
- 검색하는 컬렉션이 무작위이고 정렬되지 않은 경우 선형검색이 기본적인 검색방법
재귀(Recursion)
-
알고리즘과 방법론에서 자주 언급
-
재귀 개념은 문재를 해결하는 재호출 로직을 발견해야 함
-
재귀 호출은 스택의 개념이 적용, 함수의 내부는 스택처럼 관리
- 반복문과 스택 구조가 결합된 함수
- 파이썬 함수 → 콜스택 형태
- (단점) 재귀를 사용하면 함수를 반복적으로 호출되는 상황이 벌어져 메모리 더 많이 사용
-
재귀로 문제를 해결하는 방법
- 하위 문제를 쉽게 해결할 수 있을 때까지 문제를 더 작은 하위단위로 나누는 것을 의미
- 분할 정복법 : 하나의 문제를 분할하면서 해결하고 해결 후 하나로 다시 합치는 방법
-
재귀는 해결을 위한 특정 기능을 재호출한다는 측면
-
분할정복은 문제를 분할하고 해결하는 구체적인 방법론
→ 분할정복법을 활용하기 위해서는 재귀개념(기능 재호출)이 필요
-
-
재귀의 조건
- base case(기본 케이스 또는 조건)가 있어야 됨
- 추가 조건과 기본 케이스의 로직 차이를 확인
- 반드시 자기 자신(함수)를 호출해야 함
-
재귀 제한
-
파이썬에서는 재귀 깊이 1000으로 제한
-
재귀 함수의 호출이 1000에 도달하면
RecursionError발생→
setrecursionlimit()함수 이용해 재귀 제한 늘릴 수 있음
-
-
재귀적인 문제 해결
-
한 단계 낮은 문제가 해결된다면 그것을 바탕으로 답을 얻을 수 있
-
재귀함수 작성 시
-
재귀호출 할 때 인자를 반드시 규모가 줄어들도록 설정
-
재귀호출 없이 해결할 수 있는 최소문제(base case)설정
- 이때는 재귀호출 하지 않고 바로 답을 반환할 수 있도록 하기
-
-
트리자료구조
-
트리 용어
-
루트(root) : 가장 위쪽에 있는 노드, 트리별 하나
- 루트와 부모는 다름
- 부모노드는 자식노드가 1개 이상 있는 경우에만 존재
-
서브트리 : 자식 노드이면서 부모노드 역할을 하는 트리
- 여러 개 가능
-
차수 : 노드가 갖고 있는 최대 자식노드 수
-
리프(leaf) : 레벨별로 가장 마지막에 있는 노드
= 단말 노드(terminal node), 외부노드(external node)
- 트리별로 여러 개 가능
-
레벨 : 루트노드에서 얼마나 멀리 떨어져 있는 지, 루트노드의 레벨은 0이고 아래로 내려갈 때마다 1씩 증가
-
높이 : 루트에서 가장 멀리 떨어진 리프노트까지의 거리, 리프 레벨의 최대값
-
형제(sibling)노드 : 부모가 같은 두 개의 노드
-
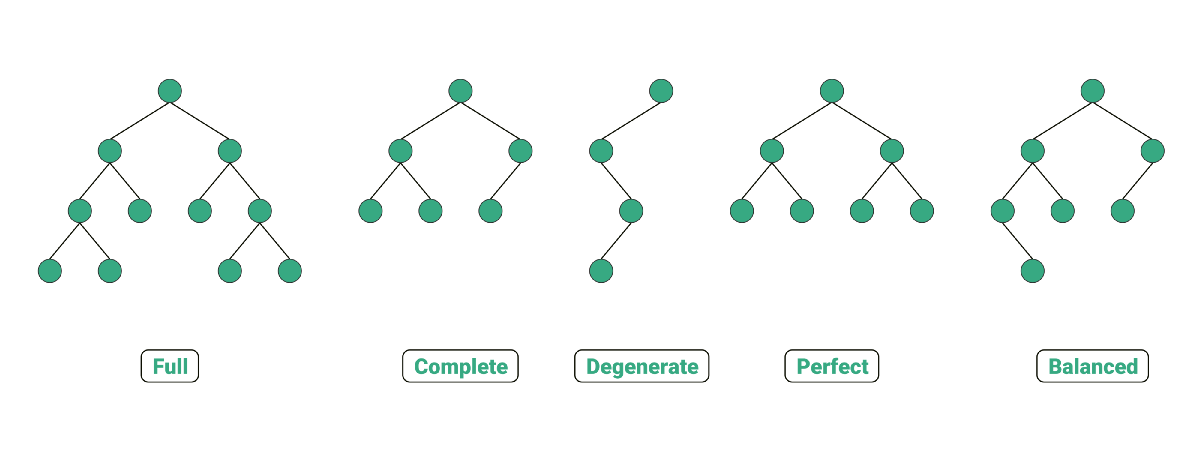
이진트리(binary tree)
-
이진트리는 각 노드별로 최대 2개의 서브노드를 가질 수 있음(left, right)
-
조건
-
루트 노드를 중심으로 두 개의 서브트리로 나눠짐
-
나눠진 두 서브트리도 모두 두 개의 서브트리를 가짐
- 서브트리의 노드가 반드시 값을 갖고 있을 필요는 없음
-
-
Perfect
- 모든 리프노드들이 동일한 레벨을 갖고 있는 경우
-
Complete
- 노드가 위에서 아래로 채워져 있고, 왼쪽에서 오른쪽 순서대로 채워져 있음
-
Binary Search Trees(BST, 이진검색(탐색)트리)
-
자식 노드가 최대 2개까지만 붙는 이진트리의 형태를 띔
-
노드를 정확하게 정렬하는 특정 유형의 이진 트리
-
조건
-
값 크기 조건 : 오른쪽 서브 노드 값 > 루트(부모)노드 값 > 왼쪽 서브 노드 값
- 중복값을 가진 노드 없어야 함
- 왼쪽 서브트리노드들의 값은 루트(부모)노드 값보다 작아야 함
- 오른쪽 서브트리노드들의 값은 루트(부모)노드 값보다 커야 함
→ 왼쪽부터 오른쪽으로 검색을 하는 구조이기 때문
-
-
특징
- 구조가 단순
- 검색하는 순서에 따라 노드값을 오름차순으로 얻음
- 검색이 쉽기 때문에 노드를 삽입하기 쉬움
- 이진탐색 트리는 정렬되어 들어오는 데이터에 약함
-
Day 3
Algorithm Fundamental
Algorithm
-
알고리즘이란?
- 특정 문제를 해결하기 위한 방법 또는 절차
- 알고리즘 → 컴퓨터에 전달 → 컴퓨터가 이해하도록 → 프로그래밍
-
프로그래밍
- 알고리즘을 프로그래밍 언어로 작성한 것
-
정렬 : 숫자 두개의 크기를 비교하고 바꿔주는 작업을 반복하여 조건에 맞게 순서를 맞춰주는 작업
- 모든 알고리즘의 기반
Search Algorithm Basic
-
선형검색(Linear search)
- 한 번에 하나씩 모두 검색
-
이진검색(Binary search)
- 정렬된 선형의 숫자들 중 특정 숫자를 효율적으로 검색하기 위해 나온 방법
- 반복을 통해 숫자를 반으로 줄이면서 검색
→ 선형검색보다 속도가 더 빠름 - 데이터가 이미 정렬된 경우에만 작동
# 처음과 마지막을 정해줘야 함 def binary_search(test_list): low = 0 # 리스트 첫번째 항목 high = len(test_list) - 1 # 리스트 마지막 항목
Iterative sorting(반복정렬)
-
Selection sort(선택정렬)
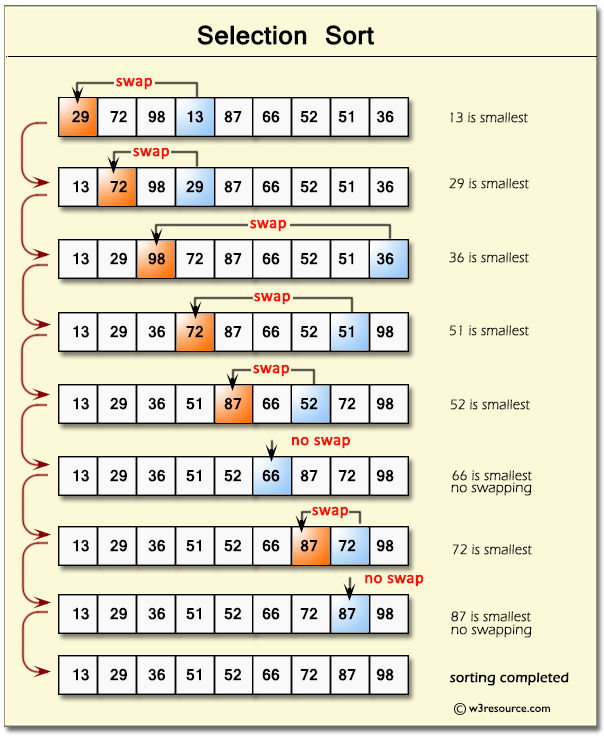
- 가장 작은 노드를 선택해 왼쪽부터 가장 작은 노드와 비교하면서 교환 시작
- 교환을 한 번 하고 나면 교환된 노드를 제외한 나머지 노드들(배열)을 기준으로 하여 가장 작은 노드를 다시 선택하고 작업을 반복
- 버블정렬과 달리 서로 이웃하지 않은 노드를 교환하므로 안정적이지 않음
- 시간복잡도 : O(n^2)
-
Insertion sort(삽입정렬)
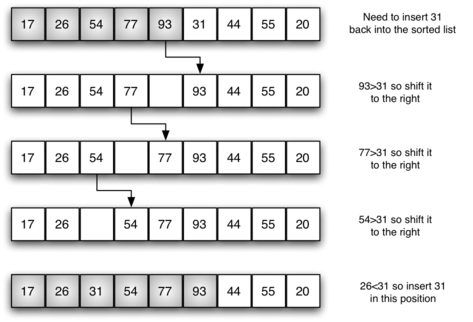
-
아직 정렬되지 않은 특정 노드와 정렬된 노드들의 값을 비교하며 값이 더 큰 것의 인덱스보다 작은 인덱스에 삽입하며 정렬
- 값이 가장 작은 원소 선택 X
- 비교 후 삽입을 동시에 진행
-
소량의 데이터를 정렬하기 위한 효율적인 알고리즘
- 선택과 버블정렬과 달리 삽입정렬은 정렬을 진행하면서 비교 및 탐색해야 할 정렬 범위가 넓어짐
-
시간 복잡도 : O(n) - 최상(이미 정렬됨), O(n^2) - 최악(반대로 정렬된 경우)/평균
-
-
Bubble sort(버블정렬)
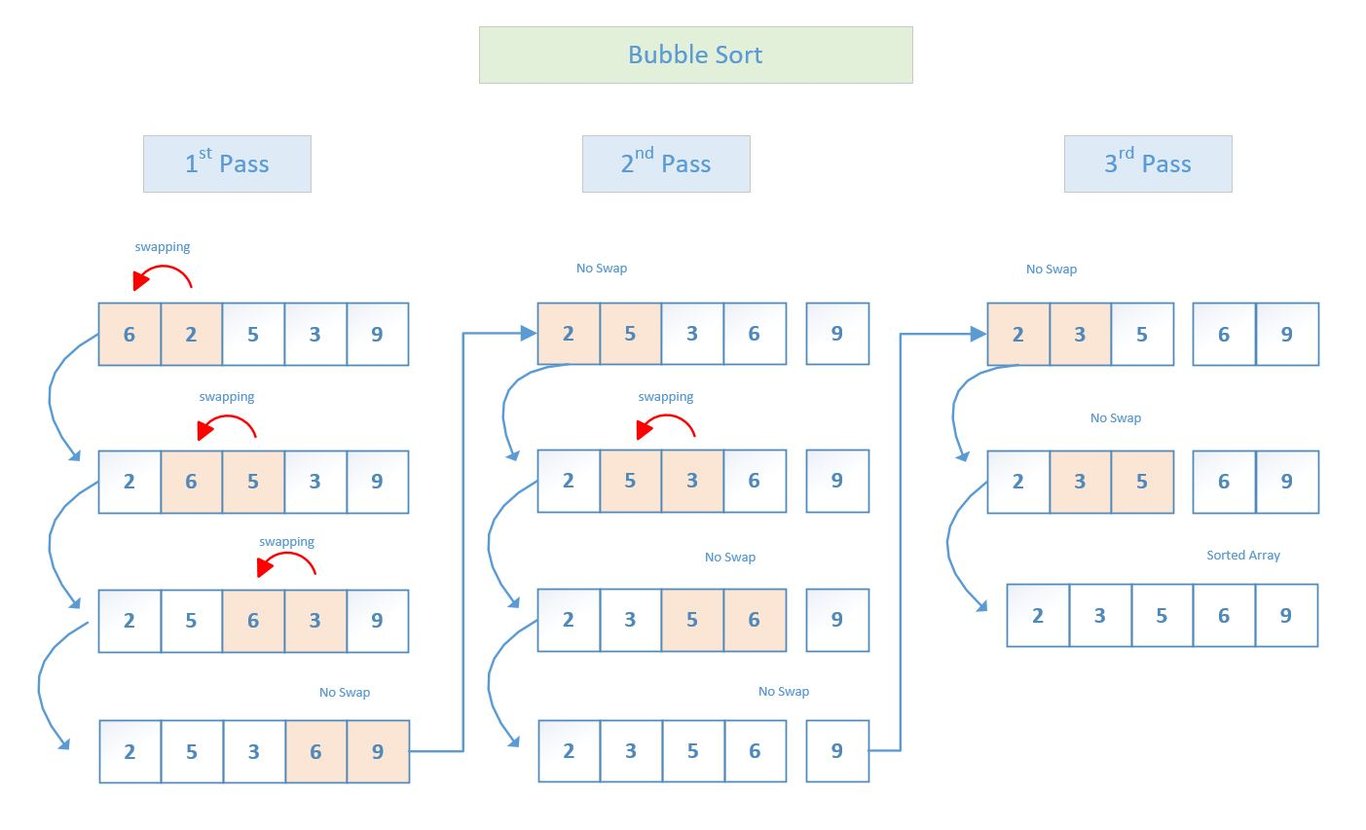
-
서로 이웃한 두 원소의 크기를 비교한 결과에 따라 교환을 반복하는 알고리즘, 단순 교환 정렬
-
가장 간단하지만 매우 비효율적
-
시간 복잡도 : O(n^2)
- 목록이 이미 정렬되어 있어도 목록의 모든 항목을 검사
- 옆에 있는 이웃노드만 교환해 안정적
-
Day 4
Algorithm Intermediate
분할정복(Divide and Conquer) 방법
-
복잡하거나 큰 문제를 여러 개로 나눠서 푸는 방법
- 병렬적으로 문제해결 가능
→ 문제 해결을 위해 문제해결함수가 재귀적으로 호출될 수 있으므로 메모리가 추가적으로 사용될 수 있음 - (장점) 어려운 문제를 작은 문제로 나눠서 어려운 문제를 쉽게 해결, 작은 문제를 분할하여 같은 작업을 더 빠르게 처리
- (단점) 함수를 재귀적으로 호출한다는 점에서 함수 호출로 인한
오버헤드발생, 스택에 다양한 데이터를 보관하고 있어야 하기 때문에스택 오버플로우가 발생하거나 과도한 메모리 사용하게 됨
오버헤드: 어떤 처리를 하기 위해 들어가는 간접적인 처리 시간/메모리 등
스택 오버플로우: 스택 포인터가 스택의 경계를 넘어설 때 발생, 프로그램이 호출 스택에서 이용 가능한 공간 이상을 사용하려고 시도할 때 스택이오버플로우된다고 함 → 프로그램 충돌 발생 - 병렬적으로 문제해결 가능
-
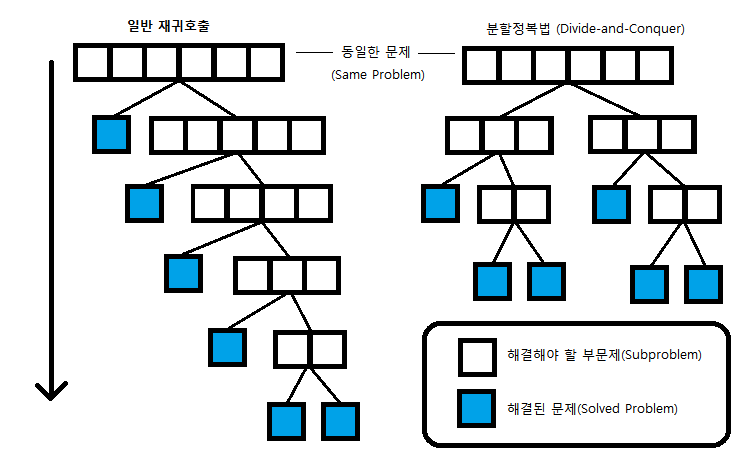
재귀호출 vs 분할정복
-
재귀호출 : 같은 함수코드를 재호출하는 것(같은 함수코드 사용)
-
분할정복 : 비슷한 작업을 재진행하는 것(같은 함수코드는 아닐 수 있음)
-
-
비슷한 크기로 문제를 분할하고 해결된 문제를 제외하고 동일한 크기로 문제를 다시 분할 → Divide , Conquer, Merge
-
분할정복 과정
- 본 문제를 서브문제로 분할(Divide)
- 서브문제의 답을 구한 경우, 해당 답을 본 문제에 대한 답이 되도록 병합(Merge)
- 문제를 분할할 수 없거나, 할 필요가 없는 경우에 대한 답을 구함(base case)
-
분할정복의 조건
- 본 문제를 서브문제로 분할할 수 있는가?
- 서브문제의 답을 병합(또는 조합)하여 본 문제의 답을 구하는 것이 효율적인가?
퀵정렬(Quick sort)
-
처음에 전체 탐색을 할 때 좌우로 나눠서 재귀적으로 수행하기 때문에 병합정렬보다 빠름
분할단계에서 정렬- 한정적인 범위에서 데이터 정렬
- 분할정복을 통해 정렬하고 피벗이라는 별도의 노드를 지정해두고 재귀적으로 수행
- 시간복잡도 : 최악 → O(n^2), 평균 → O(nlogn)
-
불안정 정렬의 대표적인 경우로 노드값이 중복되는 경우에는 계속해서 교환을 시도
- pivot을 정한 뒤 피봇보다 작으면 왼쪽, 크면 오른쪽으로 → 반복
-
최상인 경우 → O(nlogn)
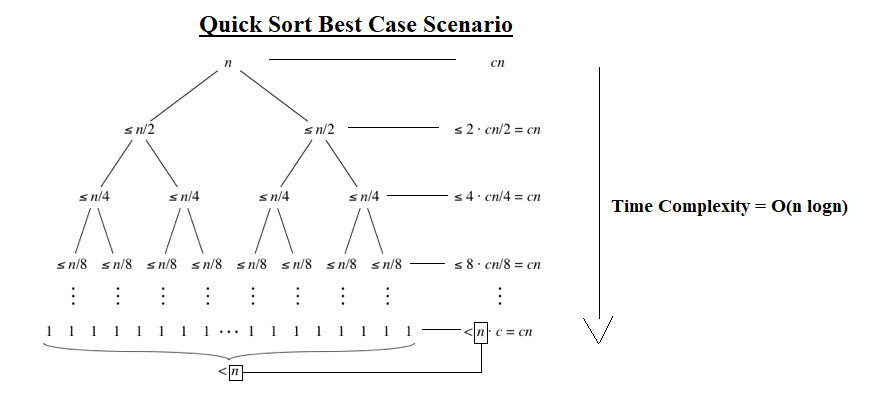
-
최악인 경우 → O(n^2)
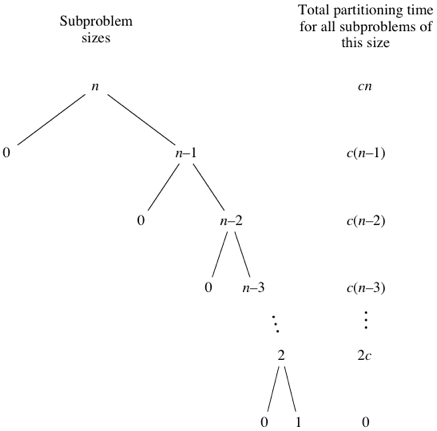
- 불균형하게 분할정복을 시도하여 성능이 안좋아짐
ㄷ
- 불균형하게 분할정복을 시도하여 성능이 안좋아짐
병합정렬(Merge sort)
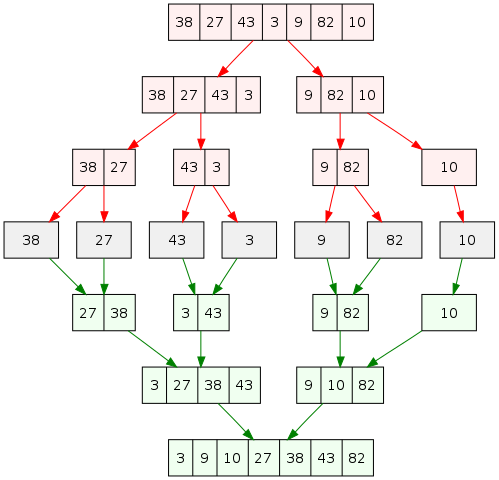
- divide and conquer 로직으로 인해 전체 데이터를 기준으로 처음과 끝을 계속해서 탐색하기 때문에 퀵소트에 비해 느림
combine할 때 정렬- 안정정렬이기 때문에 데이터가 중복되었더라도 영향 덜 받음
- 안정정렬 : 동일한 값에 대해 기존의 순서 유지
- 시간복잡도 : 항상 O(nlogn)
- 분할과 교체를 반복
- 1개의 서브리스트가 나올때까지 분할을 진행
- 이후에 배열값을 반복문을 통해 비교 → 정렬 → 후 합치는 과정을 연속적으로 진행
