LSTM(Long Short-term memory)

🔍 RNN(Simple RNN)의 한계와 LSTM의 등장 배경

✅ RNN의 핵심 구조 복습

RNN은 이전 시점의 정보를 현재 시점으로 전달하며 시퀀스 정보를 처리하는 모델이에요!
하지만 아래와 같은 심각한 한계점이 존재합니다.

---

❗ 문제점: Gradient Vanishing & 기억 소실

🔹 (1) Gradient Vanishing Problem

• RNN은 시퀀스가 길어질수록 역전파 과정에서 기울기(gradient)가 점점 작아지는 문제가 생깁니다.
• 특히 RNN에서 사용하는 활성 함수 ( \tanh )의 도함수는 항상 ( 0 \sim 1 ) 범위의 실수이므로, 곱해질수록 값이 작아집니다.
• 결과적으로 초기 time step의 정보에 대해 학습이 거의 되지 않는 현상이 발생합니다.

👉 이로 인해 긴 문장을 처리할 때, 문장의 앞부분을 제대로 기억하지 못함

🔹 (2) 기억력 소실 (Memory Decay)

• hidden state만을 사용하여 정보를 전달하기 때문에, 오랜 시간이 지나면 앞 정보는 잊히게 됩니다.
• 특히 긴 문장에서 초반에 등장한 정보는 끝까지 유지되지 못하고 소실됩니다.

---

📉 BPTT(Backpropagation Through Time)

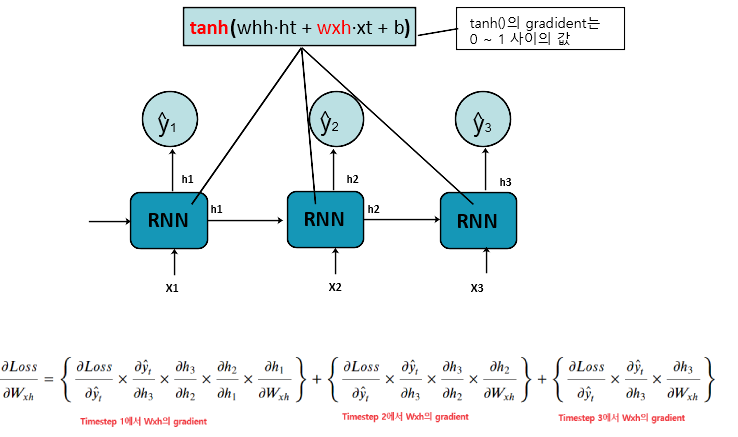
• RNN은 시간 축을 따라 펼쳐지고, 각 시점의 가중치는 공유됩니다.
• 역전파가 긴 시퀀스를 따라 갈수록, 기울기 값이 0에 수렴하면서 학습이 멈춥니다.

---

💡해결책: LSTM의 등장

"기억을 오래 유지할 수 있는 메커니즘이 필요하다!"

🔑 LSTM (Long Short-Term Memory)

• LSTM은 RNN의 구조를 확장하여, 장기 기억(long-term dependency)을 유지할 수 있도록 설계된 모델입니다.
• 핵심은 셀 상태(cell state)와 게이트(gate) 구조를 도입한 것!
  

🧠 주요 아이디어:

• 정보를 얼마나 기억할지, 얼마나 잊을지 스스로 판단할 수 있는 구조를 만듦
• 셀 상태는 각 time step을 거치며 정보가 선형적으로 흐르게 되어, 정보가 소실되지 않음

항목	Simple RNN	LSTM
기울기 소실	심각하게 발생	거의 발생하지 않음
기억 유지	짧은 구간만 가능	긴 구간까지 가능
구조	단순 (1개의 hidden state)	게이트 + 셀 상태 도입
주 사용처	짧은 시퀀스, 기초 실습	실무 모델 대부분 사용

---

LSTM의 구조

• Simple RNN과 다르게 두개의 이전 time step까지의 처리결과를 사용한다.
  - Cell State
  - Long term memory 로 전체 step에 대한 누적 기억값
  - Hidden State
  - Short term memory 로 이전 sequence 에 대한 기억값
  

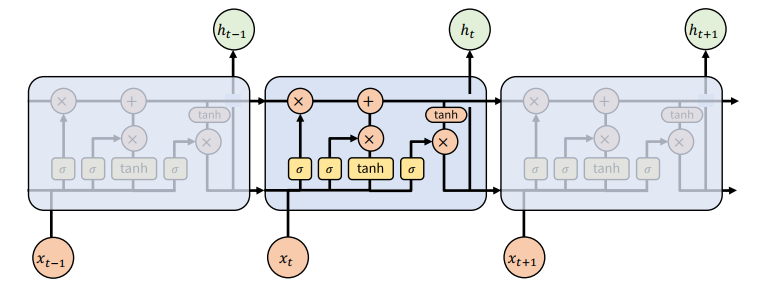
🧠 기억을 선택하는 게이트 구조

LSTM은 내부에 다음 4가지 요소가 있습니다:

• Forget Gate: 이전 정보를 얼마나 지울지 결정
• Input Gate: 새로운 정보를 얼마나 저장할지 결정
• Cell State: 장기 기억(기억 흐름)
• Output Gate: 현재 출력을 얼마나 보낼지 결정

---

🧩 Gate 연산 하나씩 살펴보기

1️⃣ Forget Gate – 잊을 것 결정

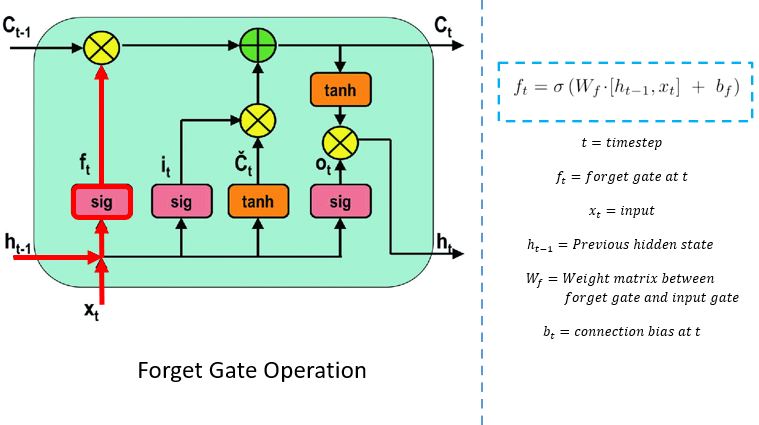
• $f_t$: Forget 게이트 출력 (0~1)
• 0에 가까우면 삭제, 1에 가까우면 유지
• 이전 셀 상태와 곱하여 기억할 정보만 유지

---

2️⃣ Input Gate – 새로 기억할 것 결정

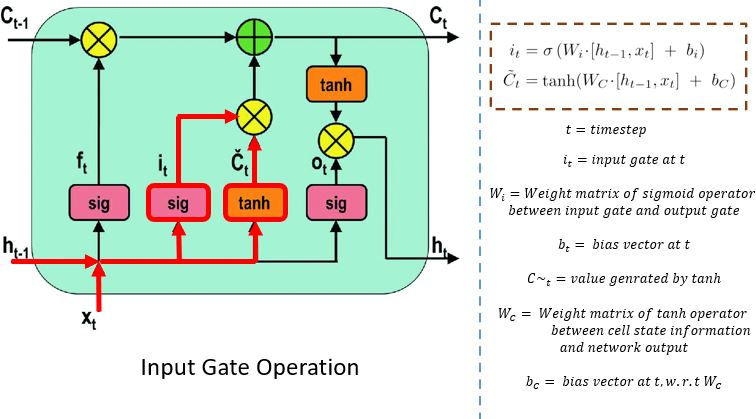
• $i_t$: 저장 비율
• $\tilde{C}_t$: 새로 기억하고 싶은 정보
• $i_t \times \tilde{C}_t$: 셀 상태에 추가할 정보

---

3️⃣ Cell State 업데이트 – 장기 기억 유지

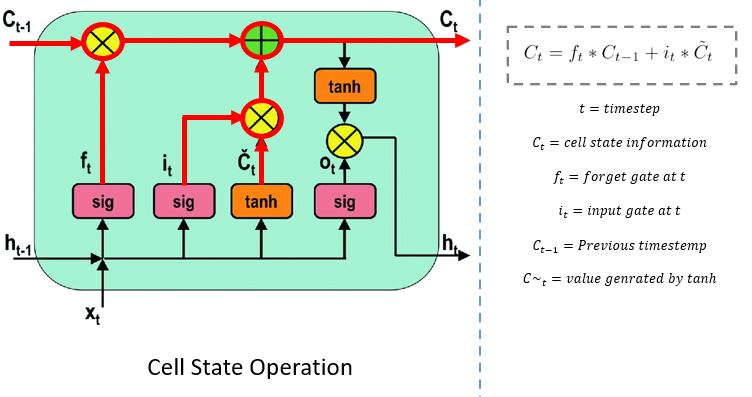
• 이전 셀 상태와 새로운 기억을 덧셈과 곱셈만으로 업데이트
• 가중치 곱 없이 정보가 전달되므로, 장기 기억 유지에 적합

---

4️⃣ Output Gate – 현재 출력 결정

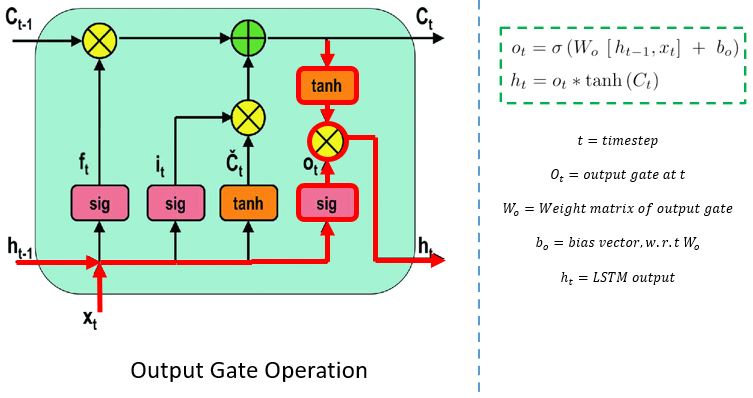
• $o_t$: 출력 게이트
• $h_t$: 현재 시점의 hidden state (= 출력값)

---

🔁 LSTM 전체 흐름 요약

게이트	계산식	역할
Forget Gate	$f_t = \sigma(W_f[h_{t-1}, x_t] + b_f)$	무엇을 잊을지
Input Gate	$i_t = \sigma(W_i[h_{t-1}, x_t] + b_i)$ $\tilde{C}_t = \tanh(W_C[h_{t-1}, x_t] + b_C)$	무엇을 기억할지
Cell State	$C_t = f_t \cdot C_{t-1} + i_t \cdot \tilde{C}_t$	장기 기억 업데이트
Output Gate	$o_t = \sigma(W_o[h_{t-1}, x_t] + b_o)$ $h_t = o_t \cdot \tanh(C_t)$	현재 출력 결정

---

✅ Gate 정리

• 모든 Gate는 입력 ( x_t )와 이전 hidden state ( h_{t-1} )를 입력으로 받음
• 각 Gate에는 고유한 가중치 ( W )와 바이어스 ( b )가 존재
• Sigmoid는 0~1 사이의 값을 출력하여 정보 통과 여부 결정
• tanh는 -1~1 사이의 값을 출력하여 정보를 조절함