
프로그래머스의 "과일 장수" 문제를 풀다가 몇몇 테스트 케이스에서 시간 초과가 발생했다. 그치만 로직 자체는 틀리지 않았다는 확신이 있었고 😅 시간 초과에 대한 원인을 분석하던 중
splice(0, m)이 원인임을 알게 됐다.
이번 글에서는 문제 풀이 과정과 시간 초과 원인 분석, 최적화 방법을 정리해보려 한다.
📝 문제 요약
- 과일 장수가
k점 이하의 사과를 팔려고 한다. m개씩 한 상자로 포장하며, 한 상자의 가격은 (가장 낮은 점수) ×m이다.- 최대한 많은 이익을 얻으려면 점수가 높은 사과부터 상자를 만들어야 한다.
⛔ 기존 코드 (시간 초과 발생)
function solution(k, m, score) {
score.sort((a, b) => b - a); // 1. 점수를 내림차순 정렬
const appleBox = [];
while (score.length >= m) {
const appleBundle = score.splice(0, m); // 2. m개씩 잘라서 새로운 배열에 저장
appleBox.push(appleBundle);
}
const answer = appleBox.reduce((prev, cur) => {
return prev + Math.min(...cur) * m; // 3. 상자의 최소 점수 × m 계산
}, 0);
return answer;
}
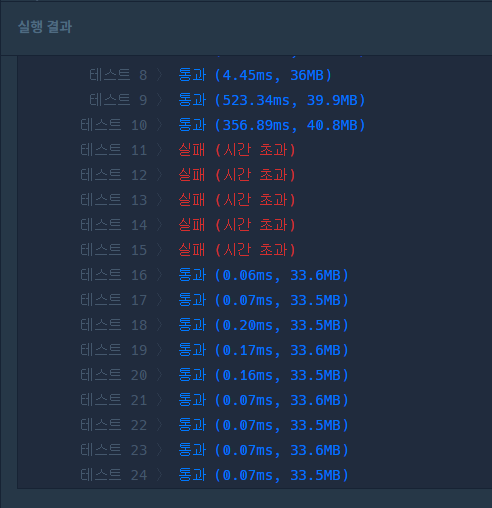
✅ 로직 자체는 맞다! 하지만
배열을 내림차순 정렬 후 m개씩 묶어 가장 작은 값을 기준으로 점수를 계산하는 로직 자체는 문제의 의도와 일치한다. 하지만 이 코드로 테스트 11~15에서 시간 초과가 발생했다.
왜일까?..^^
⏳ 시간 초과 원인 분석
1️⃣ splice(0, m) 사용 → O(n²) 발생
const appleBundle = score.splice(0, m);-
splice(0, m)는 배열의 앞부분에서m개를 잘라내므로,
남은 요소들을 한 칸씩 앞으로 당기는 과정이 필요하다. '앞에서 부터 잘라내는' 방식이 시간 복잡도를 증가시킨다는 것은 귀가 닳도록 들어왔는데 왜 까먹었지.. 일단 각설하고 -
예를 들어, score.length가 1,000,000이라면?
- 첫 번째
splice(0, m)에서 10만 개를 삭제한다고 가정하면, - 나머지 90만 개를 앞으로 이동해야 하므로 O(n) 연산 발생
- 이를 반복하면 전체적으로 O(n²)로 동작 😨
- 첫 번째
📌 O(n²)가 뭔데?
O(n²)는 빅O 표기법(Big-O Notation) 중 하나로, 이는 알고리즘의 시간 복잡도를 나타내는 표기법이다.
즉, 입력 크기(n)가 커질수록 실행 시간이 얼마나 증가하는지를 보여준다.
| 시간 복잡도 | 예제 (n=1,000,000) | 실행 시간 증가 |
|---|---|---|
| O(n) | 1,000,000번 연산 | 선형 증가 |
| O(n log n) | 약 20,000,000번 연산 | 거의 선형에 가까움 |
| O(n²) | 1조(1,000,000,000,000)번 연산 | 너무 오래 걸림 🚨 |
splice(0, m)를 여러 번 호출하면 배열의 크기만큼 반복해서 밀어야 하므로 O(n²)로 동작하게 된다.
배열 크기가 커지면 커질수록 실행 시간이 기하급수적으로 증가하기 때문에, 특정 테스트에서 시간 초과가 발생하는 것이다.
🚀 최적화된 코드 (O(n log n))
✅ splice 없이 인덱스 기반으로 접근
function solution(k, m, score) {
score.sort((a, b) => b - a); // 내림차순 정렬
let answer = 0;
for (let i = m - 1; i < score.length; i += m) {
answer += score[i] * m; // 각 상자의 최소 점수 * m
}
return answer;
}
- 그러게..
sort로 내림차순 정렬을 했으면m개씩 묶었을 때 마지막 요소가 당연히 제일 작은 수가 되는데 왜Math.min(...arr)를 또 하고 싶었는지가 참 의문이다 .. 알다가도 모를 나의 마음
⏳ 시간 복잡도 비교
| 코드 | 시간 복잡도 | 주요 연산 |
|---|---|---|
| 기존 코드 | O(n²) | splice(0, m)로 배열을 계속 이동 |
| 개선 코드 | O(n log n) | sort 후 for 루프만 사용 |
💡 배열을 직접 조작하지 않고, 인덱스로 접근하면 O(n log n)으로 최적화 가능
📌 회고
✅ 배열 조작 (splice, slice) 사용 시 성능을 항상 고려하자!
✅ 인덱스로 접근하는 방식이 splice보다 빠를 수 있다. for loop와 메서드를 적재적소에 쓰는 감을 익히자!
✅ 시간 초과가 난다고 로직이 틀린 건 아니다! 최적화만 하면 된다! 기죽지 마!
