회귀분석 정리
중간에 식 쓰기 귀찮아서 원래 필기 해 두었던 자료 링크 첨부
여기 아마 대부분 증명 해 놓았던 것으로 기억함.
https://github.com/google-official/pdfs/tree/main/regression
SAS 더이상 사용 안하는데 code는 https://velog.io/@jj770206/SAScodes-Regression 이정도면 충분하다고 생각
1. Linear Regression
회귀분석 : 설명변수 ( 독립변수 ) 에 대응하는 반응변수 ( 종속변수 ) 를 예측하는 라는 식에서의 parameter인 를 찾습니다.
그 중 선형 회귀 분석은 의 식이 에 관한 linear combination일때를 의미 합니다. 많이 하는 실수는 이 들어가면 선형이 아니라고 하는데 선형은 의 linearity를 의미하므로 선형회귀직선이 맞습니다.
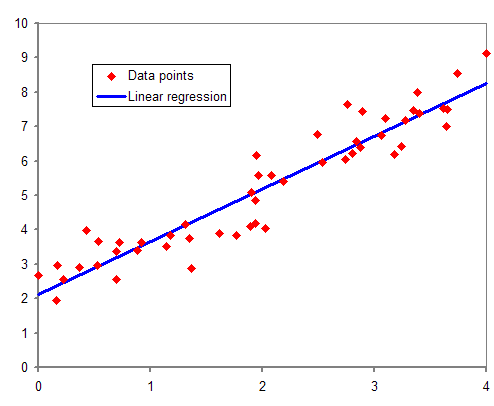
위와 같이 빨간색 점들이 data이고 이를 의 값이 주어졌을 때 를 예측하는 함수를 만든다고 가정해 보겠습니다.
이때는 정확히 이라고 하겠습니다.
즉, 파란색 직선을 만들어야 합니다. 함수를 만들기 위해서는 이 필요합니다.
어떠한 기준에 의해 직선식을 구했다는 것은 과 을 구했다는 의미 입니다.
따라서 예측직선은 =+라고 표현될수 있으며 의 값이 들어온다면 =+으로 예측 될 수 있습니다.
여기서 하나 생각할 수 있는 사실은 는 입니다. 즉 위에서 언급한 특정한 기준을 만족시키는 라는 것이 모집단에서 존재합니다. 반대로 과 는 입니다. 즉, 표본으로 부터 모수를 추정하기 위해 계산된 입니다. 따라서 expectation, variance, distribution을 구할 수 있고 가설 검정이 가능하며 CIL, CLM을 구할 수 있습니다.
statistic, R.V, parameter에 대해 추가설명
Residual
이제 위에서 말한 기준이 무엇인지 보겠습니다.
http://www.ssacstat.com/default/cs/cs_05.php?com_board_basic=read_form&com_board_idx=356&topmenu=5&left=5&&com_board_search_code=&com_board_search_value1=&com_board_search_value2=&com_board_page=&
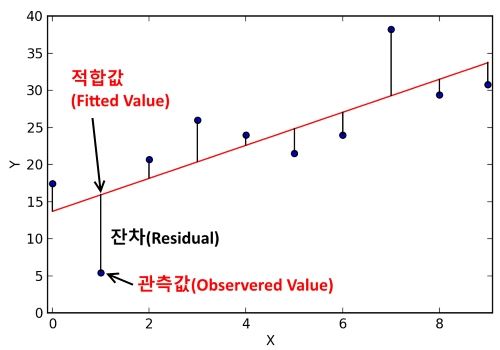
기준을 알기 전에 잔차라는 개념을 먼저 알아야 합니다.
위의 에서 을 오차항 이라고 합니다. 이는 우선 가정해야합니다. 이 가정이 있어야 앞으로 전개될 등의 내용이 성립할 수 있습니다.
오차항과 비슷한 것이 잔차 ( Residual )입니다. 잔차는 다음과 같습니다.
즉, 실제 값에서 추정된 직선을 이용한 추정값을 뺀 값입니다.
위의 그림에서 쉽게 알 수 있습니다.
즉, 잔차가 클 수록 추정된 직선은 실제 데이터와 멀리 떨어져 있습니다. 따라서 우리는 위에서 말한 기준을 오차들의 제곱합으로 합니다.
즉, 을 loss function으로 해주면 됩니다.
즉, 이제 를 위의 loss를 이용하여 구할 수 있습니다. loss를 최소화 해주는 가 이 됩니다.
이는 closed form으로 쉽게 계산이 됩니다.
즉, 와 으로 각각 미분하여 정규방정식이 0이 되는 를 찾으면 됩니다. 다만 0이 된다고 무조건 minimum은 아니므로 미분을 사용하여 구하려면 Hessian matrix까지 구해야 합니다.
다른 방법으로는 식 자체를 제곱하여 구하는 방법이 있습니다.
주의
하나 다시 유의할 점은 바로 아래 나오고 뒤에 가설검정 나오는데 이게 문제가 오차에 대한 가정이 있을때만 분포 가정이 성립합니다.
ANOVA
제곱합 분해라고 합니다. (위의 github에서 regression에도 있는데 matrix와 multi에더 잘해놓음.)
(d.f 같은거 위의 깃허브 들어가면 다 증명 해 놓음.)
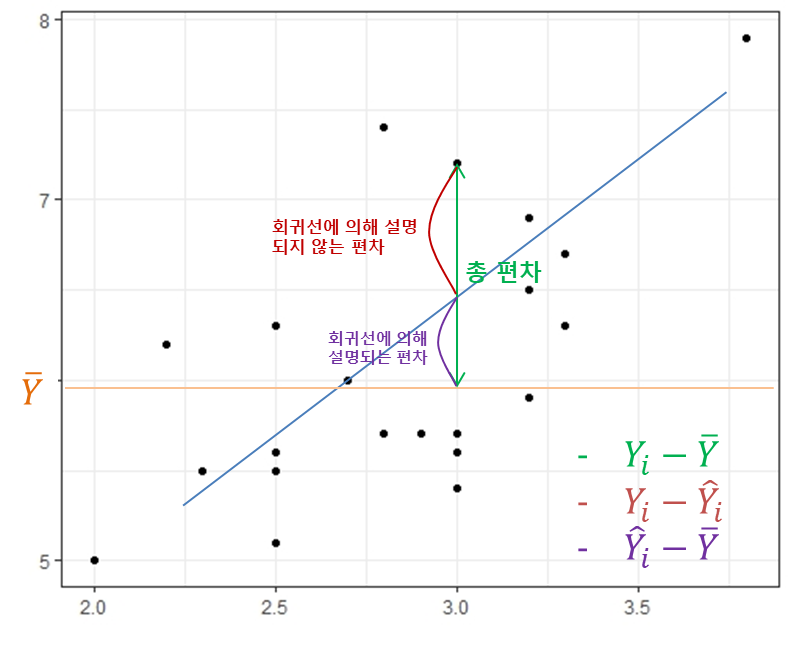
제곱한 분해는 평균 보정 안하고 하는 것도 있는데 회귀에서는 평균 보정하여 사용하고 위의 table을 ANOVA라고
이를 총변동 = 추정된 직선으로 설명되는 부분 + 추정된 직선으로 설명되지 못하는 부분
이라고 이해할 수 있습니다. ( LSE가 SSE입니다. )
이때 SSE가 회귀직선이 설명하지 못하는 부분입니다. 그래서 LSE로 사용한다고 봐도 됩니다. 작으면 좋습니다.
2. Regression Diagnostics
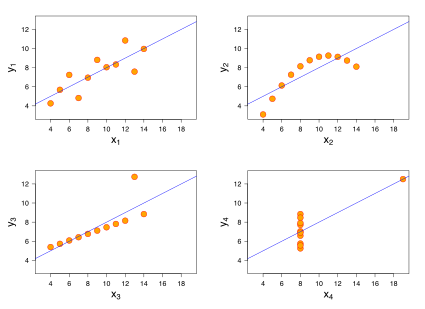
위의 과정으로는 를 추정할 수 있었습니다. 근데 정당성이 없습니다. 이를 다른말로 하면 어떠한 data든 선형회귀직선을 구할 수 있다는 것입니다.
사진을 보면 첫번째를 제외하고는 선형직선을 적합하는 것이 틀린 것 처럼 보입니다. 하지만 위에서 정한 LSE를 이용하여 추정은 가능합니다. 따라서 우리가 적합한 직선을 타당성을 만들어야 합니다.
회귀모형은 크게 4가지의 기본 가정이 있습니다.
- 설명변수와 반응변수의 선형성
- 오차의 정규성
- 오차의 등분산성
- 오차의 독립성
즉, 모형을 적합하였다면 위 4가지 가정을 다시 검정해야 합니다.
선형성
data의 scatter plot을 그려보면 됩니다.
이떄 선형관계가 아니라면 적절한 변수 변환을 이용하면 됩니다.정규성
잔차의 Histogram과 QQ plot을 그려보면 됩니다.
등분산성
설명변수에 대한 잔차그림을 크려 확인합니다. 이분산성이면 테일러 전개를 이용하여 분산 안정화 변환을 합니다.
독립성
residual plot에서 patter이 있으면 독립성이 깨집니다 또한 더빈왓슨 검정이나 ACF를 이용하여 판단합니다.
모형선택
위의 검정을 통과하였다면 모형을 선택해야 합니다. 그러면 또 기준이 필요합니다.
- 모형선택기준
- F - test
- t - test
- Durbin - Watson
1.
결정계수라고 합니다.
이때 는 총 변동 , 은 적합된 회귀선으로 설명 가능한 변동 이었습니다. 따라서 결정계수는 큰것이 좋습니다. 하지만 data의 개수가 많아지면 결정계수가 커지므로 이를 보정한 것이 adj 입니다.
2. F - test
위에서 는 statistic이라고 하였습니다. 즉, 가설검정, CLI가 가능합니다.
위의 ANOVA tabel에서 F-Stat이라고 된 부분이 F-value입니다. 이는 유의성 검정이라고도 불립니다. 이는 정확히 다음과 같은 가설의 test statistic입니다.
라는 가설검정입니다.
가설검정을 간단하게 설명하면 에서 Distribution이 정의되고 이에 samapling을 통해 나온 값이 test statistic입니다. 또한 유의수준 가 주어진다면 기각역이 주어지는 것이므로 test statistic이 충분히 커거 기각역에 속한다면 (p-value가 보다 작다면) 를 지지할 만한 충분한 증거가 발견되지 못하였음을 의미합니다.
즉, F-value가 충분히 크다면 를 기각합니다. 이떼 를 다시보면 적합된 모든 이 0이라는 의미인데 이는 적합된 회귀직선이 의미 없다는 것을 의미합니다. 즉, F-value가 크다면 회귀직선이 유의미 한것으로 판단 할 수 있습니다.
추가로 왜 F-test를 하는지 설명하자면, 과 마찬가지로 모두 statistic입니다. 즉, 분포를 가지고 있습니다. (위의 깃하브 matrix에 증명 있음) 이를 이용하여 의 분포를 구하면 F 분포가 나옵니다.
(엄밀한 증명은 상당히 까다로움)
3. t - test
F - test는 모든 회귀계수를 한번에 검정하였다면 t - test는 각각의 회귀계수에 대해 가설검정을 진행합니다. 여기까지 보면 다음과 같이 생각할 수 있습니다. "t - test를 모든 변수에 대해 검정하면 F - test와 같지 않나?" 결론은 같지 않습니다. 위에서 F분포를 증명할 때 조건 하에서면 가능했습니다. (아마 카이제곱 비중심뭐 그런거였던거 같음.) 반대로 t -test는 를 설정할 때 가 굳이 0이 아니어도 분포가정이 성립합니다. 즉, 유의성 검정은 전체 모형의 유의성을 판단하는데 사용되며 t -test는 각 회귀 계수 검정에 사용된다고 생각하면 됩니다. 이렇게 쓰임이도 차이가 있지만 정확하게 수리적으로도 차이가 있습니다. ( 이 부분이 잘 기억이 안나는데 무슨 conditional 어쩌구였던거 같음. 나중에 다시 찾아보고 정리함.)
그래서 정리해 보면 이고 이떄 test statistic은 저 위에 깃허브에 있음.
Durbin - Watson
시계열에서 많이 나오는데 자기상관성 검정 통계량입니다. 결론은 0~4가 아노는데 2이면 자기상관성이 없는것이고 0이면 양 4이면 음의 자기상관성 입니다.
변수변환
변수변환을 통해 선형성을 만족시킬수 있습니다. 또한 등분산성을 만족시킬 수 있습니다.
다중공선성
설명변수간의 상관관계가 높아서 생기는 문제 입니다. 회귀분석은 설명변수 간의 독립을 가정합니다. 그런데 이 독립성이 깨지게 되면 문제가 발생합니다. 즉, 상관성이 높은 두개의 설명변수로 하나의 반응 변수를 설명 하기 떄문에 생기는 문제 입니다.
- 정확하게 다음과 같은 문제가 있습니다.
- 첫번째로 회귀계수 추정이 불안정합니다.
- 분산이 매우 커집니다.
이므로 분산이 매우 커져서 t - value가 작게 나타납니다. 따라서 를 기각하지 못합니다.
다중공선성 진단
COV 계산을 하거나, VIF를 구하면 됩니다.
VIF는 설명변수간의 회귀적합을 한 후 결정계수를 구한 것입니다.
다중공선성 제거
- 상관성이 높은 두 변수를 각각 제거해 보고 결정 계수가 유지되는 변수를 남기고 나머지 제거
- etc,.....
3. Logistic Regression
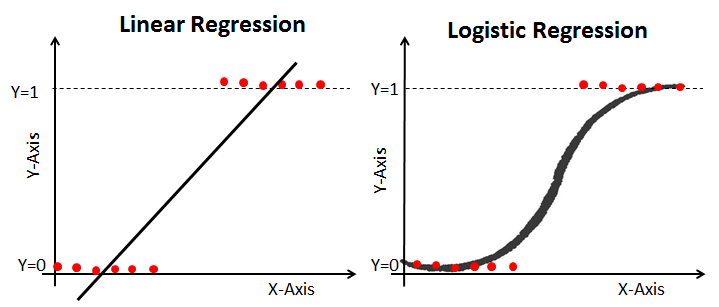
위와 같이 반응변수가 범주형이면 왼쪽과 같이 선형회귀는 적절하지 않습니다. 따라서 이를 곡선으로 바꿔주기 위해 Logistic Function을 도입합니다.
입니다.
즉, 모수는 입니다.
이는 선형회귀와는 다르게 MLE를 이용하여 추정합니다.
추정
4. Metrics for classification (Binary)
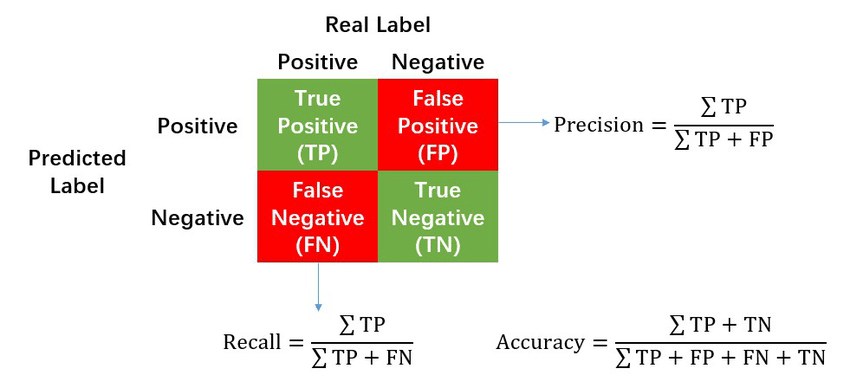
Precision and Recall
https://www.researchgate.net/figure/Calculation-of-Precision-Recall-and-Accuracy-in-the-confusion-matrix_fig3_336402347
즉, 정밀도는 모델이 True라고 분류한 것들 중 실제로 True인것의 비율이고
재현율은 실제로 True인것 들중 모델이 True라고 분류한 것의 비율이다.
두개의 지표는 trade-off관계이다.
Accuracy란 전체 데이터중 정답과 같은 예측을 한 것들의 비율이라고 보면 된다. 이는 치명적인 단점있다. 예를들어 어떤 데이터는 90개의 T와 10개의 F로 이루어져 있다고 해보자. 그리고 이를 예측하는 모델은 이상해서 input에 관계없이 무조건 T라고 예측한다고 해보자. 그러면 이 모델의 Acc는 90%이다. 따라서 데이터가 편향되어있다면 좋지 않은 지표이다.
F1 Score
Precision과 Recall의 조화평균이다.
ROC Curve
5. 추가
선형 회귀에서 catagorical variable이 존재하는 경우.
해결 방법 위의 깃허브 "회귀아마중간정리에기말추가한거.pdf"에서 마지막에서 3번째 정도에 나옴.
6. 정리
순서
1. Check data
결측치 확인, data구조 확인 ( 변수명 등등 ), type확인 후 catagorical이변 변환.
scatter plot, 기초통계량, 반응변수의 분포 ( histogram, box plot), 모든 변수별 pairplot ( heat map ), cov matrix2. Fit model
1번에서 나온 정보를 이용하여 model을 세우고 적절한 loss을 이용하여 parameter를 fitting.
전체 변수의 유의성 검정, 각 변수의 t-value, 결정계수, ANOVA Table 등을 확인3. Diagnose
이렇게 fitting 할 수 있었던 이유는 선형성, 오차의 정규성 ( N(0,k) ), 등분산성, 독립성을 가정 하였기 때문.
따라서 이 4가지 가정이 맞는지 확인해줘야 함.
1. 선형성
이건 처음에 scatter plot즉, 다중회귀있때는 pair plot이용하여 확인함.
2. 잔차분석
이건 fitting 이후에 확인할 수 있음. 즉, 원래는 오차에 대한 분석이 맞지만 sample data로 구한 residual을 error의 statistic이라고 생각하여 residual을 분석한다.
Residual hiostogram, QQ-plot -> 정규성 판단.
설명변수 X별로 residual plot ( 또는 X를 fitted y로 대신해도 같음. )-> 등분산성 판단, 독립성 판단, 선형성 판단
ACF, Durbin - Watson -> 자기상관성 확인
VIF -> 다중공선성 확인.
이러한 결과를 가지고 model을 수정하여 다시 적합하는 과정을 반복.
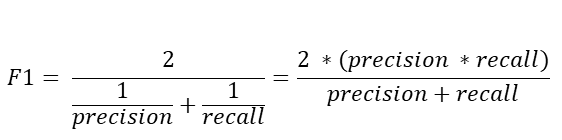
.png)