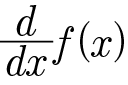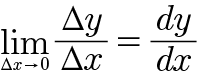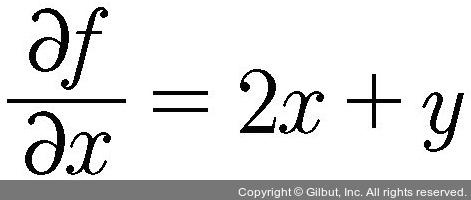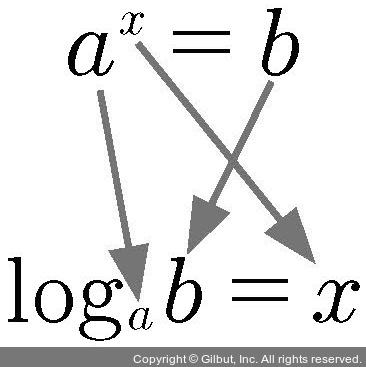* 딥러닝 실행 전 준비사항
1) 미지의 일을 예측하는 원리
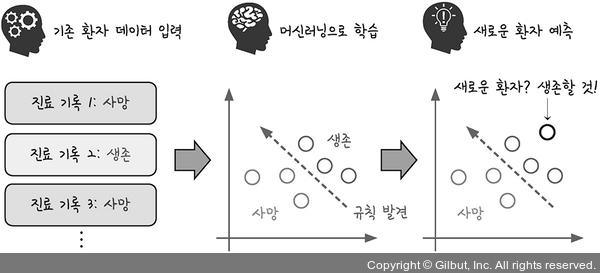
- 머신러닝 : 데이터들 속에서 규칙을 찾아내고 새로운 데이터에 적용해 새로운 결괏값 도출 ➡️ 기존 데이터를 활용해 아직 일어나지 않은 일들을 예측
- 학습(Learning) : 데이터가 입력되고 패턴이 분석되는 과정
- 예측 성공률 : 얼마나 정확하게 경계선을 긋는지에 달려있음
* 딥러닝 개괄
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 딥러닝 구동하는데 필요한 케라스 함수 호출
import numpy as np
import tensorflow as tf
# 필요한 라이브러리 불러오기
np.random.seed(3)
tf.random.set_seed(3)
#실행할때마다 같은 결과 출력
Data_set = np.loadtxt('...', delimiter=',')
# 준비된 데이터 불러오기
X = Data_set[:, 0:17]
Y = Data_set[:,17]
# 학습데이터와 결과 데이터로 나눔
model = Sequential()
model.add(Dense(30, input_dim=17, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
#딥러닝 모델 구조 결정 및 생성
model.compile(loss = 'mean_squared_error', optimizer='adam', metrics=['accuarcy'])
model.fit(X, Y, epochs=100, batch_size=10)
# 딥러닝 실행- loss : 실패할 확률
- accuarcy : 성공할 확률
1) 데이터 분석과 입력
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 딥러닝 구동하는데 필요한 케라스 함수 호출
import numpy as np
import tensorflow as tf
# 필요한 라이브러리 불러오기
np.random.seed(3)
tf.random.set_seed(3)
#실행할때마다 같은 결과 출력
Data_set = np.loadtxt('...', delimiter=',')
# 준비된 데이터 불러오기
X = Data_set[:, 0:17]
Y = Data_set[:,17]
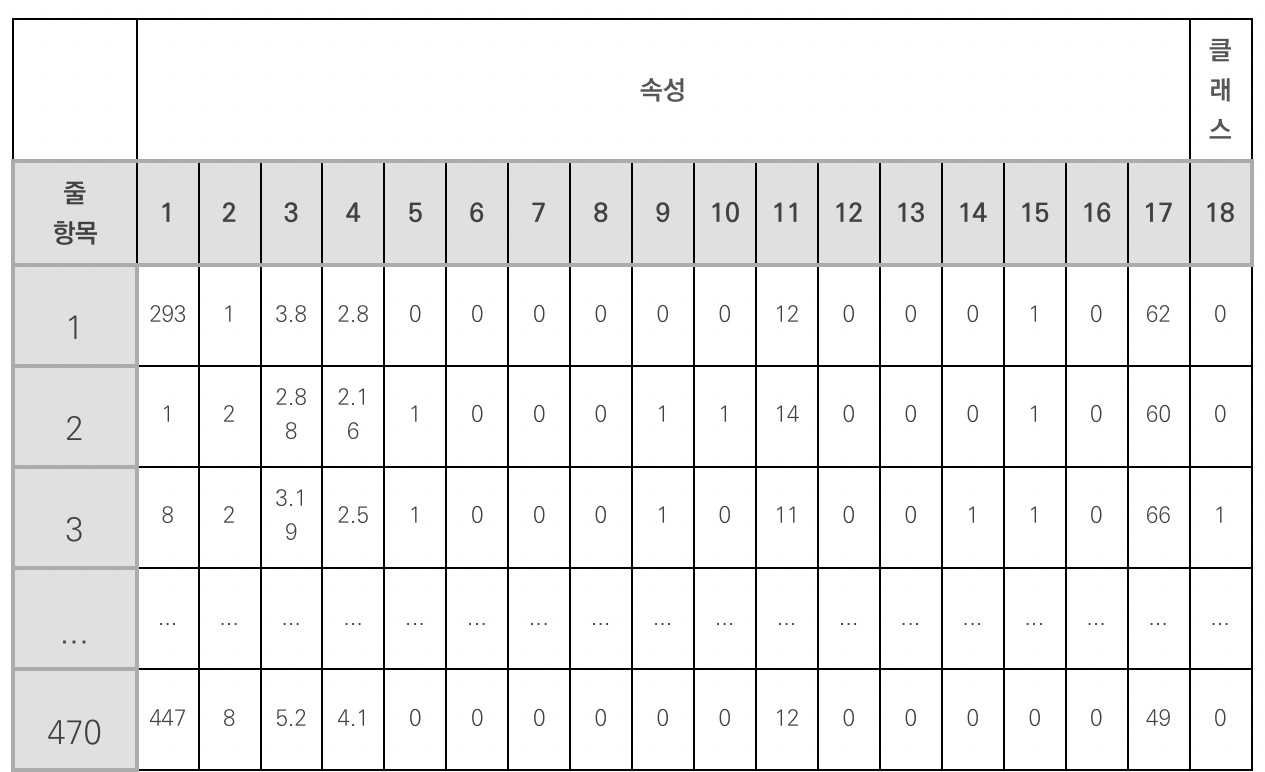
# 학습데이터와 결과 데이터로 나눔- Data_set
- [0:17] : 속성(attribute) ➡️ 분석할 데이터
- [17] : 클래스(class) ➡️ 데이터 정답값
2) 딥러닝 실행
model = Sequential()
model.add(Dense(30, input_dim=17, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
#딥러닝 모델 구조 결정 및 생성
model.compile(loss = 'mean_squared_error', optimizer='adam', metrics=['accuarcy'])
model.fit(X, Y, epochs=100, batch_size=10)
# 딥러닝 실행- Sequential() 함수 선언 후 add를 통해 레이어를 겹겹이 쌓아 올림
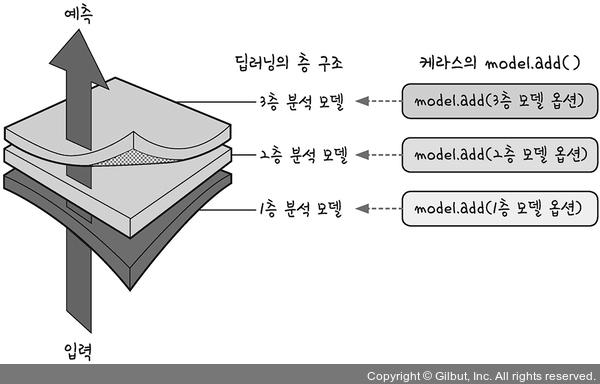
- Dense() : 각 층의 특성 설정
- activation : 다음 층으로 어떻게 값을 넘길지 설정
- compile()
- loss : 신경망이 실행될때마다 오차를 추적하는 함수
- optimizer : 오차를 어떻게 줄여나갈지 결정
1. 딥러닝을 위한 기초 수학
1) 미분
- 이차함수에서 최솟값을 구하기 위해서는 미분값이 필요함
미분 : 순간변화율 구하기!
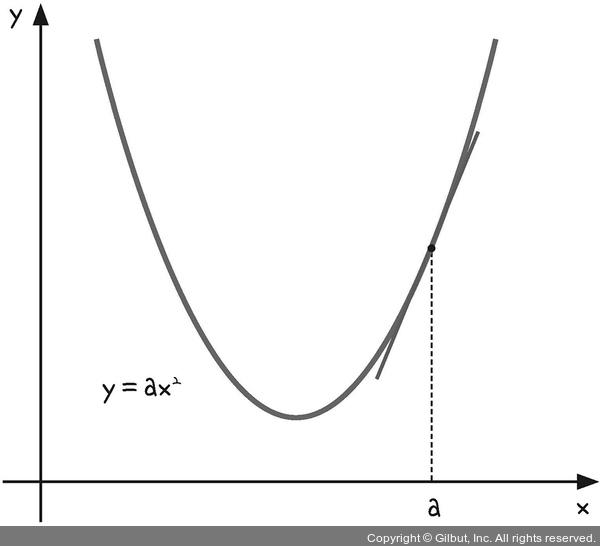
- 기울기 : 방향성을 지니기 때문에 방향을 따라 직선을 길게 그려주면 a에 접하는 접선의 형태로 만들어짐
- 미분계수 = 그래프에서의 기울기
- 기울기 0 : 그래프의 최솟값
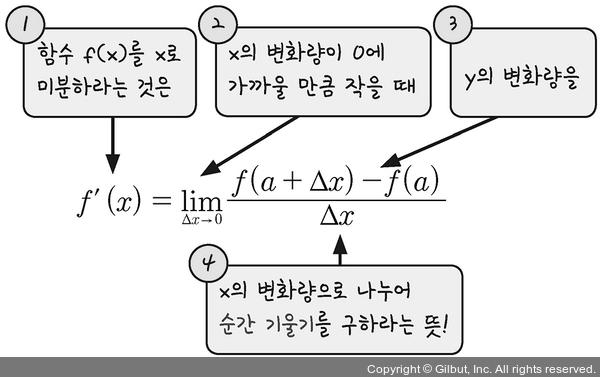
- ✔️ 평균변화율 : 두 점 A, B의 기울기
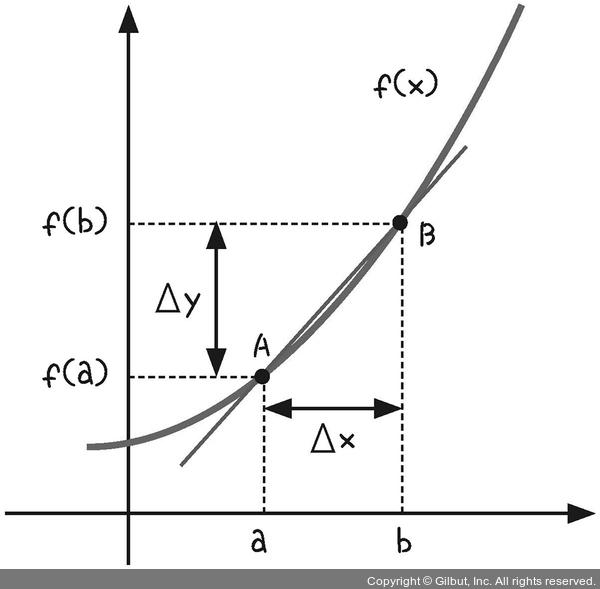
- x 증가량 : b - a = ∆ x
- y 증가량 : f(b) - f(a) = f(a+∆ x) - f(a)
- 기울기 : y 증가량 / x 증가량

- ✔️ 평균변화율 : 두 점 A, B의 기울기
- ✔️ 순간변화율 : x 증가량이 0에 가까울 만큼 아주 작을 때의 순간적인 기울기
- f'(x) = 함수 f(x) 미분
- 미분 특징
1️⃣ f(x) = a 에서 a가 상수일 때 미분값 = 0
2️⃣ f(x) = x 일 때의 미분값 = 1
3️⃣ f(x) = ax에서 a가 상수면 미분값 = a
4️⃣ f(x) = x^a 일 때 a가 자연수면 미분값 = ax^a-1
2) 편미분
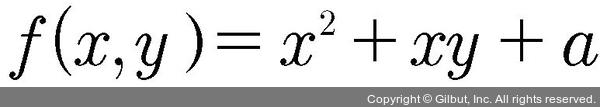
✔️ 편미분 : 어떤 변수로 미분할 지 결정
- x에 관해서 편미분할 경우, 아래와 같은 식이 나옴
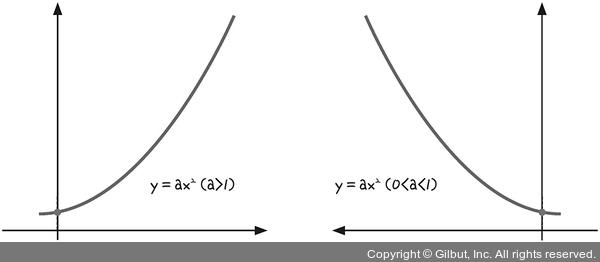
3) 지수

- a : 밑
- x : 지수
- a를 x만큼 반복해서 곱
✔️ 지수함수 : x가 지수 자리에 있는 경우 ➡️ a의 값에 따라 그래프 모양이 달라짐
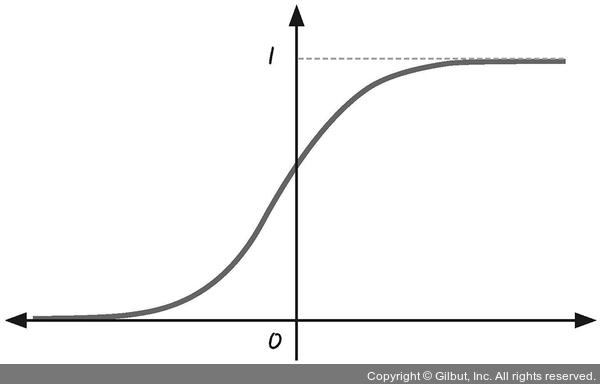
4) 시그모이드 함수
✔️ 시그모이드 함수 : 지수함수에서 밑 값이 자연 상수 e인 함수
- x값이 큰 값을 가지면 ➡️ f(x)는 1에 가까워짐
- x값이 작은 값을 가지면➡️ f(x)는 0에 가까워짐
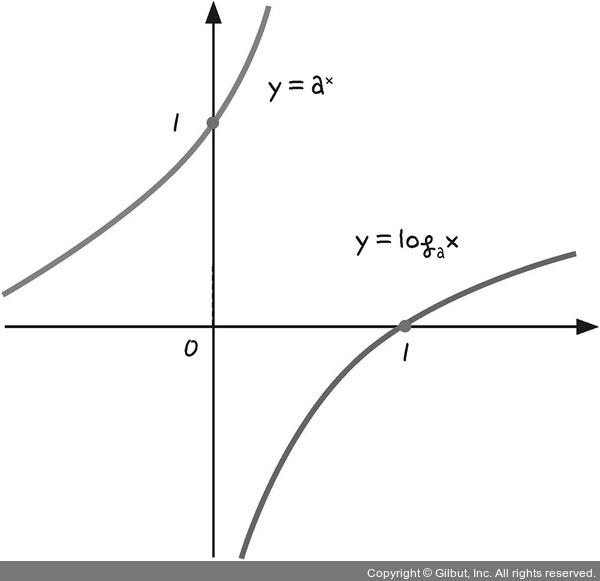
5) 로그 함수
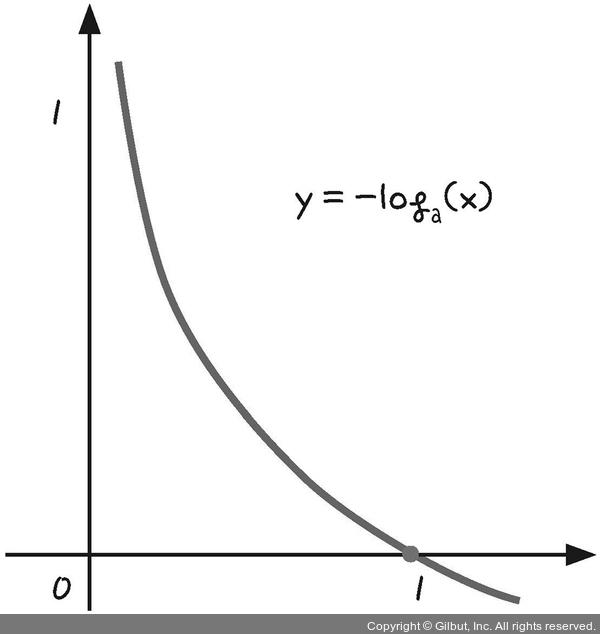
✔️ 로그 함수 : 지수함수와 역관계
- y = x에 대해 대칭인 선으로 나타남
- 로그 함수의 대칭이동
1️⃣ x축에 대하여 대칭 이동
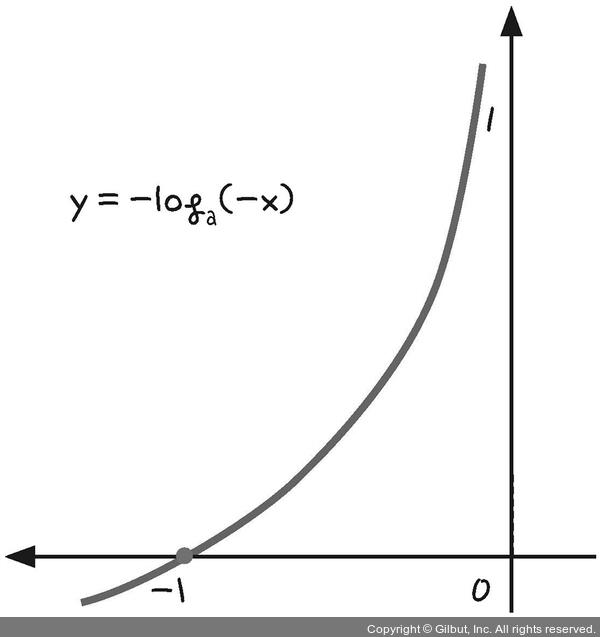
2️⃣ x축과 y축에 대해여 대칭 이동
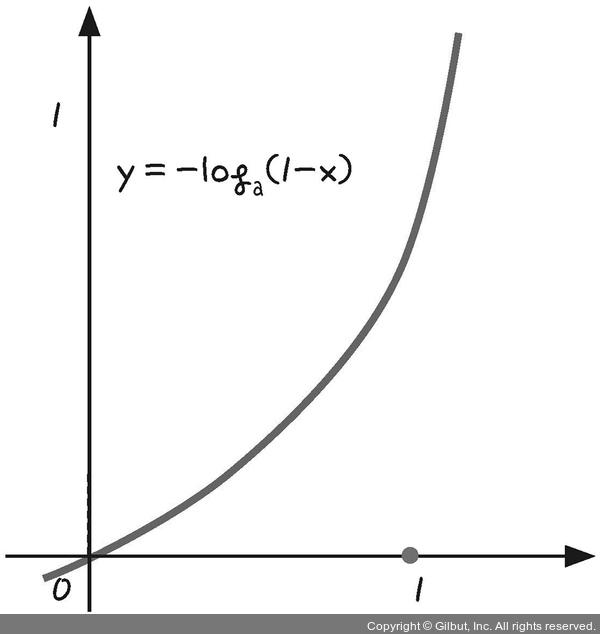
3️⃣ 위 그래프를 x축 방향으로 1만큼 이동
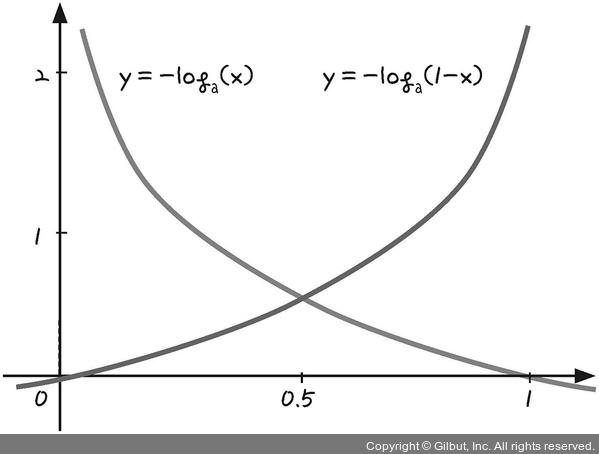
4️⃣ 1, 3번 그래프 동시에 나타내기