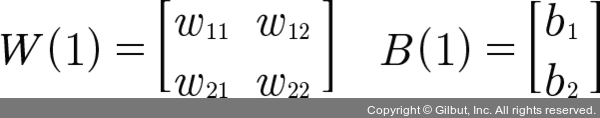1. 퍼셉트론
- 신경망을 이루는 가장 기본적인 구조
- 뉴런과 시냅스
- 뉴런 : 신경계를 구성하는 세포
- 시냅스 : 뉴런과 뉴런을 연결(입력에 의해 자극을 받아 다른 뉴런으로 정보 전달)
- 입력 : 여러개의 자극들로 구성
- 입력들은 기준치 이상을 달성해야 전달함(모두 전달하는 건 아님)
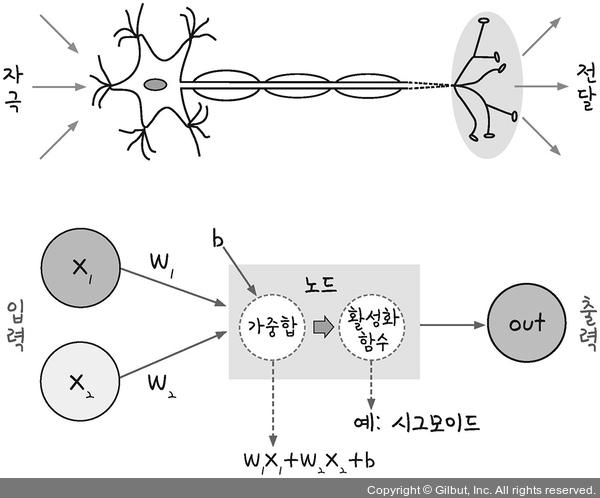
- 퍼셉트론 : 입력값과 활성화 함수를 통해 출력값을 다음으로 넘기는 가장 작은 신경망 단위
1) 가중치, 가중합, 바이어스, 활성화함수
-
로지스틱 회귀 == 퍼셉트론
y = ax + b ➡️ y = wx + b(w는 가중치, b는 바이어스)
- 가중치(weight) :
- 바이어스(bias) : 편향
- 가중합(weighted sum) : 입력값 x와 가중치 w를 곱하고 바이어스 b를 더함
- 활성화 함수(activation) : 가중합의 결과를 보고 0과 1을 판단
* 퍼셉트론의 한계
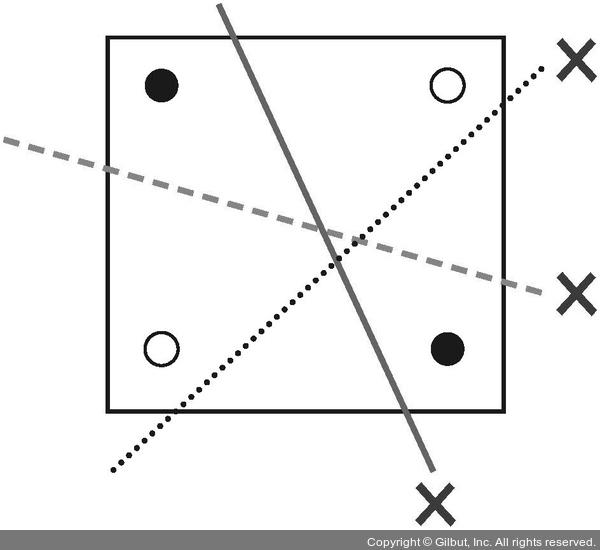
- 직선 한 개만으로는 색 구분 불가능
* XOR 문제
- 게이트(gate) : 컴퓨터의 두 가지의 디지털 값, 즉 0과 1을 입력해 하나의 값을 출력하는 회로
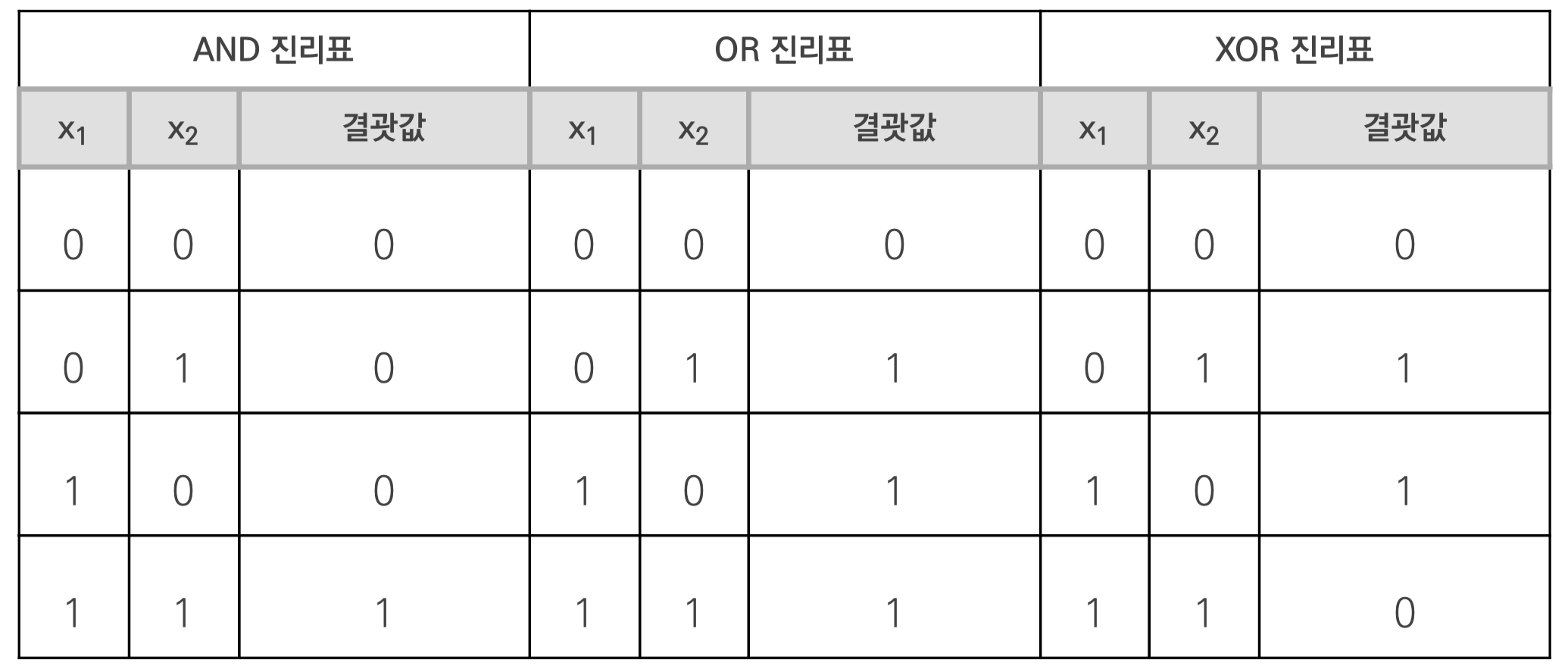
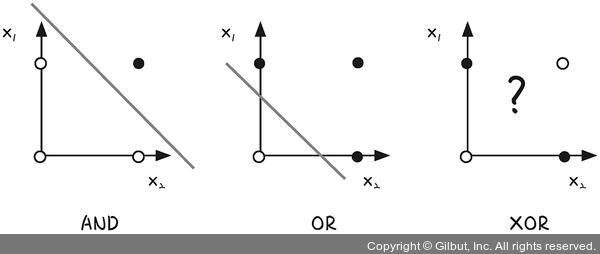
- AND, OR 연산 : 한 개의 직선으로 결과값 구분 가능
- XOR : 구분 불가능
2) 다층 퍼셉트론
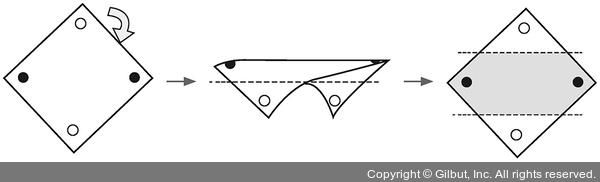
- 좌표 평면 자체에 변화를 주면 됨
- XOR 문제 해결 : 2개의 퍼셉트론 한 번에 계산
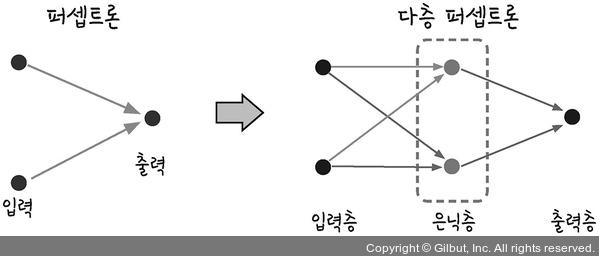
- 은닉층(hidden layer)
- 은닉층이 평면을 왜곡시키는 결과를 가져옴
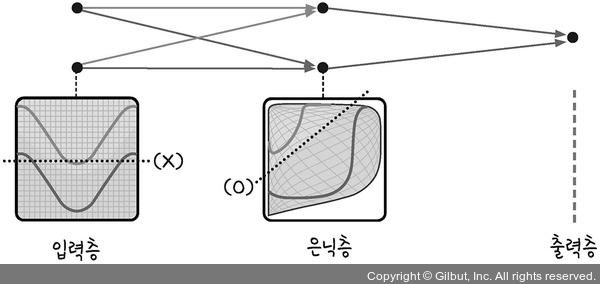
- 은닉층이 평면을 왜곡시키는 결과를 가져옴
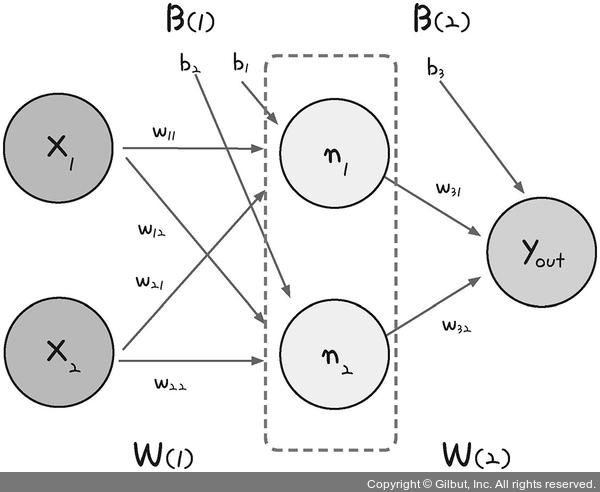
<1> 다층 퍼셉트론 설계
- 퍼셉트론이 은닉층으로 가중치와 바이어스를 보냄
- 은닉층으로 모인 값은 시그모이드함수(σ) 이용하여 최종값으로 결과를 보냄
- 노드(node) : 은닉층에 모이는 중간 정거장(n1, n2)
- 단일 퍼셉트론의 값 계산
n1 = σ(x1w11 + x2w21+b1)
n2 = σ(x1w12 + x2w22 + b2)- 출력층의 값 계산
- 각각의 가중치와 바이어스
<2> XOR 문제 해결
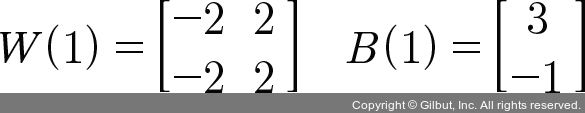

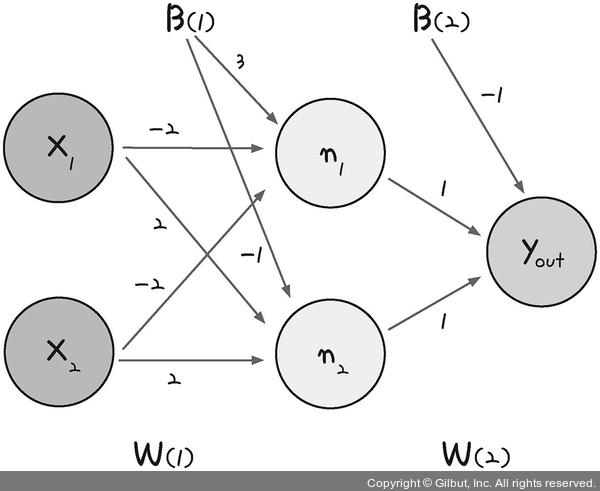
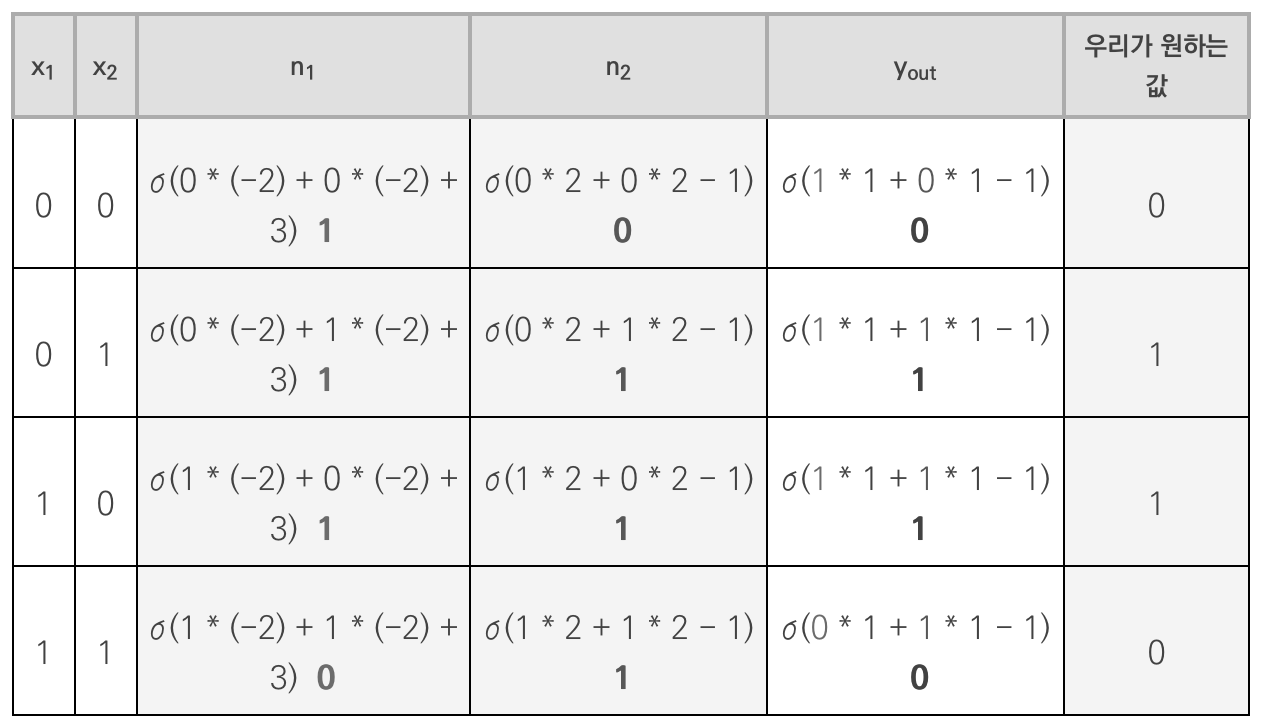
- n1 gate : AND gate의 정반대값 출력함 ➡️ NAND(Negative AND) Gate
- n2 gate : OR gate
- y gate : AND gate
<3> 코드
import numpy as np
w11 = np.array([-2,-2])
w12 = np.array([2,2])
w2 = np.array([1,1])
b1 = 3
b2 = -1
b3 = -1
def MLP(x,w,b): #퍼셉트론 함수
y = np.sum(w*x)+b
if y <= 0:
return 0
else:
return 1
def NAND(x1, x2):
return MLP(np.array([x1,x2]), w11, b1)
def OR(x1, x2):
return MLP(np.array([x1, x2]), w12, b2)
def AND(x1, x2):
return MLP(np.array([x1, x2]), w2, b3)
def XOR(x1, x2):
return AND(NAND(x1,x2), OR(x1,x2))
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = XOR(x[0], x[1])
print("입력 값: " + str(x) + " 출력 값: " + str(y))def MLP2(x, w, b):
ws = x.dot(w) + b
return ws > 0
w1 = np.array([[-0.5,0.5],[-0.5,0.5]])
w2 = np.array([0.5,0.5])
b1 = np.array([0.7,-0.2])
b2 = np.array([-0.7])
X = np.array([(0, 0), (1, 0), (0, 1), (1, 1)])
for x in X:
n = MLP2(x, w1, b1)
y = MLP2(n, w2, b2)
print("입력 값: " + str(n) + " 출력 값: " + str(y))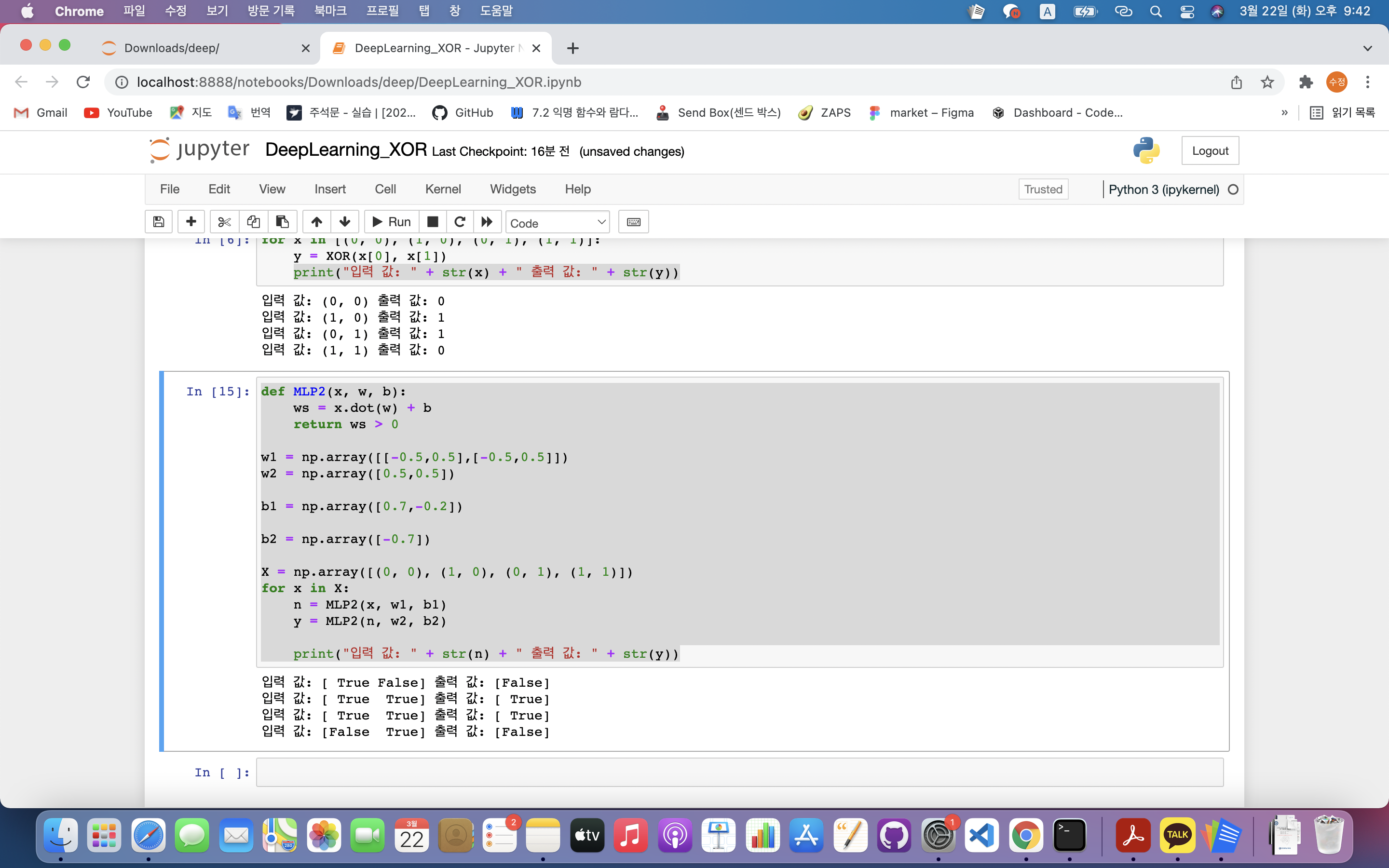
3) 오차 역전파(back propagation)
- 신경망 내부 가중치 수정
- 경사하강법의 확장 개념
- 다층 퍼셉트론에서의 최적화 과정
- 임의의 가중치 선언 후 결괏값을 이용해 오차를 구함. ➡️ 오차가 최소의 지점으로 계속해서 이동시킴
- 오차가 최소가 되는 지점 : 우리가 찾는 정답임
1️⃣ 단층 퍼셉트론 : 입력층, 출력층으로만 구성
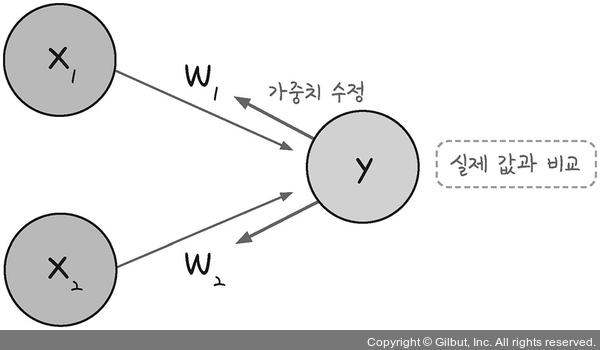
2️⃣ 다층 퍼셉트론 : 은닉층 존재 ➡️ 결괏값 오차를 토대로 하나 앞선 가중치를 차례로 거슬러 올라가며 조정
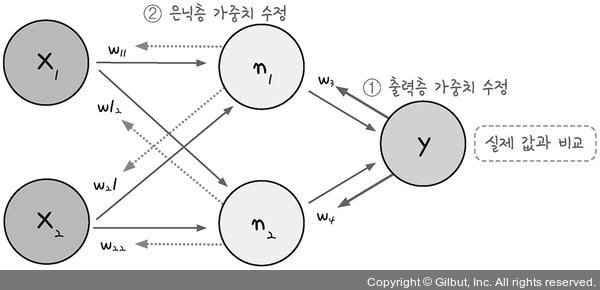
- 절차
- 1️⃣ 임의의 초기 가중치(W)를 준 뒤 결과(y) 계산
- 2️⃣ 계산 결과와 원하는 값 사이의 오차 구하기
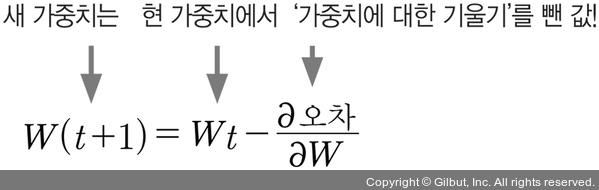
- 3️⃣ 경사 하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트
- 기울기가 0이 되는 방향으로 이동
- 가중치에서 기울기를 뺐을 때 가중치의 변화가 전혀 없는 상태
- 4️⃣ 위 과정을 오차가 더이상 줄어들지 않을 때까지 반복
알고리즘
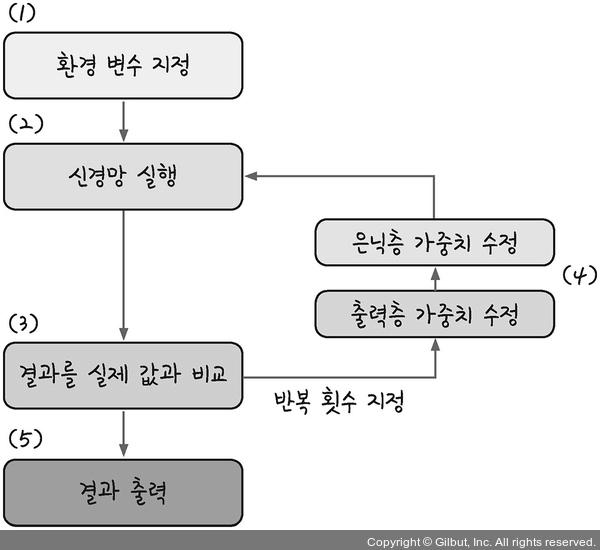
1️⃣ 환경 변수 지정 : 입력값, 타깃 결과값이 포함된 데이터셋, 학습률 등 포함. 또한, 활성화 함수, 가중치 등도 선언
2️⃣ 신경망 실행 : 초깃값을 입력하여 활성화 함수와 가중치를 거쳐 결괏값이 나오게 함
3️⃣ 결과를 실제 값과 비교 : 오차 측정
4️⃣ 역전파 실행 : 출력층과 은닉층 가중치 수정
5️⃣ 결과 출력
2. 딥러닝
- 다층 퍼셉트론 + 오차 역전파 = 신경망
- 신경망을 쌓으면 인공지능의 성능이 올라갈까? 안 올라감
1) 기울기 소실 문제와 활성화 함수
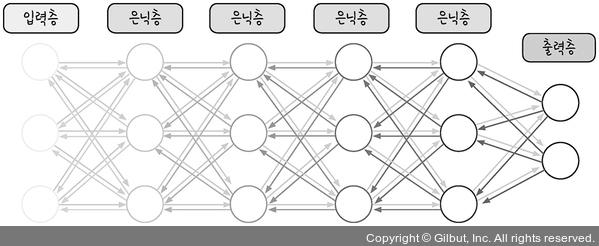
- 기울기 소실 문제(vanishing gradient)
- 가중치 수정하려면 미분 값(기울기) 필요
- 층이 늘어나면 역전파를 통해 전달되는 기울기 값들이 점차 작아져서 맨 처음층까지 도달 시 기울기가 소실되는 문제 발생
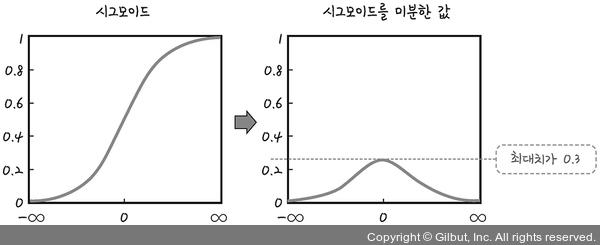
➡️ 활성화 함수가 시그모이드 함수이기 때문 : 미분값이 1보다 작아지기 때문에 지속적으로 곱할 경우 0에 가까워짐.
✔️ 다양한 활성화 함수 도입
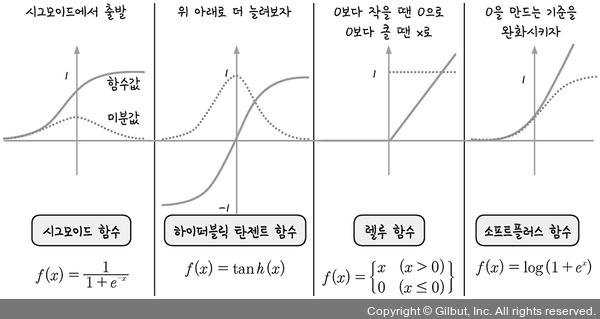
- 1️⃣ 하이퍼블릭 탄젠트 함수
- 시그모이드 함수 범위 확장 : -1 ~ 1로 확장
- 여전히 1보다 작은 값이 존재함
- 2️⃣ 렐루 함수
- 시그모이드 함수 대안으로 사용 : 가장 많이 사용되고 있음
- x < 0 : 모든 값은 0으로 처리
- x > 0 : 모든 값에 대하여 y=x
➡️ 미분값이 1이 됨.
➡️ 여러 은닉층을 거쳐 곱해져도 맨 처음층까지 값이 존재하게 됨
- 3️⃣ 소프트 플러스 함수
- 렐루 함수 변형
- 렐루가 0이 되는 순간을 완화
2) 고급 경사 하강법
- 경사하강법 : 가중치 업데이트를 위해 전체 데이터를 매번 미분해야 하므로 계산량이 매우 많음
➡️ 고급 경사하강법 등장
<1> 확률적 경사 하강법(Stochastic Gradient Descent, SGD)
- 전체 데이터를 사용하는 것이 아니라 랜덤하게 추출한 일부 데이터 사용 ➡️ 일부 데이터만 사용하기 때문에 더 빨리, 자주 업데이트 가능해짐.
- 경사 하강법 : 불필요하게 많은 계산으로 인해 속도가 느리고, 최적의 해를 찾기 전까지 최적화 과정이 멈추지 않음
- 빠른 속도, 최적값에 근사한 값을 찾아냄

<2> 모멘텀(momentum)
- 경사 하강법에 탄력을 더해줌
- 경사하강법을 통해 기울기를 구하며, 그 과정에서 오차를 수정하기 전 바로 앞 수정값과 방향(+,-)를 참고하여 같은 방향으로 일정한 비율만 수정하게 됨
- 즉, 이전 이동값을 고려해 일정 비율만큼만 다음값을 결정하므로 관성의 효과를 낼 수 있음.

<3> 딥러닝 구동에 사용되는 고급경사하강법
3-1) 확률적 경사 하강법(SSG)
- 개요 : 랜덤하게 추출한 일부 데이터를 사용해 더 자주, 빨리 업데이트하는 방법
- 효과 : 속도개선
- 케라스 사용법 :
keras.optimizers.SGD(lr=0.1)
3-2) 모멘텀(Momentum)
- 개요 : 관성의 방향을 고려해 진동과 폭을 줄임
- 효과 : 정확도 개선
- 케라스 사용법 :
keras.optimizers.SGD(lr=0.1, momentum=0.9)
3-3) 네스테로프 모멘텀(NAG)
- 개요 : 모멘텀이 이동시킬 방향으로 미리 이동해서 그레이디언트 계산. 불필요한 이동을 줄이는 효과
- 효과 : 정확도 개선
- 케라스 사용법 :
keras.optimizers.SGD(lr=0.1, momentum=0.9, nesterov=True)
3-4) 아다그라드(Adagrad)
- 개요 : 변수의 업데이트가 잦으면 학습률을 적게 하여 이동보폭을 조절
- 효과 : 보폭 크기 개선
- 케라스 사용법 :
keras.optimizers.Adagrad(lr=0.01, epsilon=1e-6)- 참고 : epsilon, rho, decay 같은 파라미터 안 바꾸고 그대로 사용하기. ➡️ 학습률 값만 적절히 조절
3-5) 알엠에스프롭(RMSProp)
- 개요 : 아다그라드 보폭 민감도 보완
- 효과 : 보폭 크기 개선
- 케라스 사용법 :
keras.optimizers.RMSProp(lr=0.01, rho=0.9, epsilon=1e-6, decay=0.0)
3-6) 아담(Adam)
- 개요 : 모멘텀 + 알엠에스프롭
- 효과 : 정확도와 보폭 크기 개선
- 케라스 사용법 :
keras.optimizers.Adam(lr=0.01, beta_1 = 0.9, beta_2=0.999, epsilon=1e-6, decay=0.0)