[백준 1655] 중앙값 빠르게 찾는 알고리즘

문제 요구 사항

https://www.acmicpc.net/problem/1655

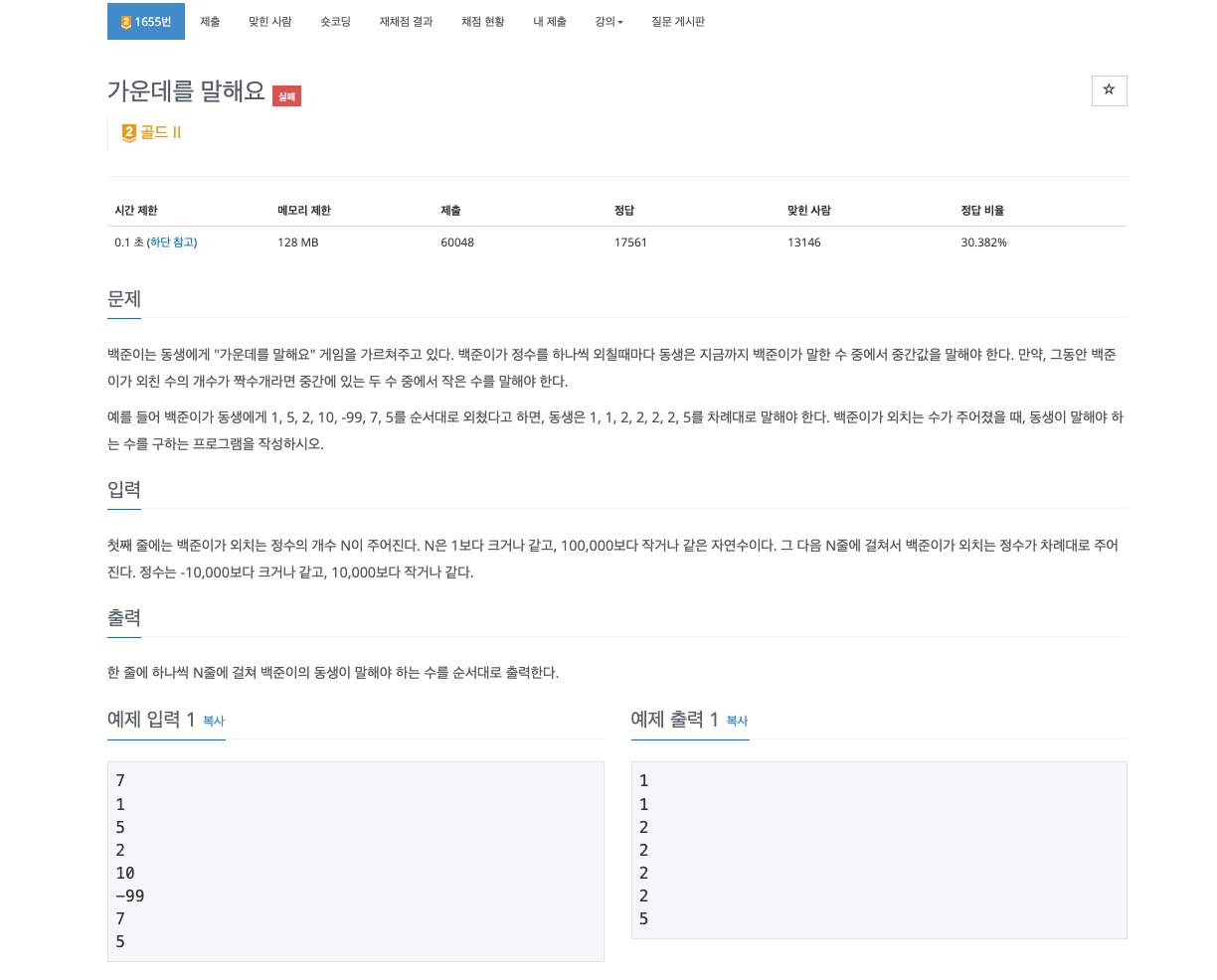
• 값이 N개가 주어진다.
• 값이 하나씩 주어질 때마다, 지금까지 입력된 값들 중 중앙값을 찾아서 출력한다.
  - 중앙값을 출력하기 위해서는 입력값이 들어올 때마다 정렬되어 있어야 함.
• 시간 제한은 0.1초, N은 100,000보다 작거나 같은 자연수
  

---

알고리즘 접근 회로

🤔 무식하게 접근

무식하게 생각해보자. 중앙값을 출력하기 위해서는 입력값이 들어올 때마다 정렬되어있어야 한다.

그렇다면, vector<int> v에 값을 입력 받고, 값을 입력 받을 때 마다 sort(v.begin(),v.end())하면 되지 않을까?

하지만 N의 값이 100,000이기 때문에 시간 초과가 날 것이라는 것을 확인 할 수 있다.

• $sort(v.begin(), v.end()) => O(N*log(N))$
• $N\space times => O(N)$
• $Total => O(N^2*log(N))$

만일 $N$이 $100,000$이라면, $O(N^2*log(N)) = 50,000,000,000$

시간이 엄청나게 오래 걸릴 것이다.

🥲 sort()를 호출 하지 않는다면?

그럼 매번 입력값이 들어올 때마다 vector에 정렬된 채로 값을 넣는다면? 나는 이 알고리즘이 정답일 줄 알고, 바로 코드를 작성해서 제출했다.

#include <bits/stdc++.h>
using namespace std;

vector <int> v;

void insertNewNumber(int n) {
    const auto pos = lower_bound(v.begin(), v.end(), n);
    v.insert(pos, n);
}

int main (void)
{
    int N, next;

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr); cout.tie(nullptr);

    cin >> N;
    for (int i = 0; i < N; i++) {
        cin >> next;
        insertNewNumber(next);

        int midIdx = (v.size() - 1) / 2;
        cout << v[midIdx] << '\n';
    }

    return 0;
}

깔끔하게 시간 초과 났다.

값을 한번 계산해보고 접근했다면, 이런 실수를 하지 않았으리라.

• $New\space Input => O(N)$
• $N\space times => O(N)$
• $Total => O(N^2)$

만일 $N$이 $100,000$이라면, $O(N^2) = 10,000,000,000$
사실 값을 비교해보면 무식하게 풀었을 때와 5배 밖에 차이나지 않는다.

정렬하는 시간에서 $O(N*log(N))$을 $O(N)$로 바꿨다고 문제가 해결 될 거라고 생각했지만, $O(log(N))$은 정말 미미한 숫자에 불과 했다..

👀 우선순위 큐를 사용해보자

https://www.crocus.co.kr/625

우선순위 큐를 통해서 값을 집어넣고 읽는 것은 다음과 같다.

$priority\space queue\space INSERT = O(log(N))$
$priority\space queue\space DELETE = O(log(N))$
$priority\space queue\space READ = O(1)$

따라서 우선순위 큐를 사용해서 코드를 작성한다면 조금 더 빠르게 알고리즘을 완성할 수 있었다.

• $New\space Input => O(logN)$
• $N\space times => O(N)$
• $Total => O(N*log(N))$

만일 $N$이 $100,000$이라면, $O(N^2) = 500,000$

#include <bits/stdc++.h>
using namespace std;

priority_queue<int, vector<int>, less<int>> pqGreater;
priority_queue<int, vector<int>, greater<int>> pqLess;

int main (void)
{
    int N, num;

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr); cout.tie(nullptr);

    cin >> N;
    for (int i = 0; i < N; i++) {
        cin >> num;
        
        if (pqGreater.empty()) {
            pqGreater.push(num);
        }
        else if (pqGreater.size() == pqLess.size()) {
            pqGreater.push(num);
        }
        else if (pqGreater.size() > pqLess.size()) {
            pqLess.push(num);
        }

        if (!pqGreater.empty() && !pqLess.empty() && (pqGreater.top() > pqLess.top())) {
            int fromGreater = pqGreater.top();
            int fromLess = pqLess.top();

            pqGreater.pop();
            pqLess.pop();

            pqGreater.push(fromLess);
            pqLess.push(fromGreater);
        }

        cout << pqGreater.top() << '\n';
    }

    return 0;
}