1. 검색 알고리즘
- 학습목표: 주어진 배열 속에서 특정 값을 찾는 방법을 설명할 수 있다.
- 핵심단어: 선형검색, 이진검색
-- 선형검색, 이진검색 : 정렬 X, 정렬 O
2. 알고리즘 표기법
- 학습목표: 알고리즘의 실행시간의 상한과 하한을 표기할 수 있다.
- 핵심단어: Big O, Big Ω
1) Big O
-- 알고리즘을 수행하는데 필요한 시간의 상한선을 의미 (최악의 경우)
2) Big Ω
-- Big O 와 상반되는 관계 (최상의 경우)
Big O Big Ω O (n²) selection sort
bubble sortselection sort bubble sort———— ————— ————— O (n log n) merge sort merge sort ———— ————— ————— O (n) linear search bubble sort ———— ————— ————— O (log n) binary search - ———— ————— ————— O (1) - linear search
binary searchbubbble sort 의 경우, 더 이상 교환이 일어나지 않을 때 멈추는 최적화 기법이 존재한다면 소요 시간이 줄어들어 하한선이 낮아짐
3. 선형 검색
- 학습목표: 주어진 배열 또는 구조체에서 선형검색을 할 수 있다.
- 핵심단어: 선형검색, 구조체
- 자바와 동일하게 문자열을 비교할 때 비교연산자를 사용할 수 없음
- strcmp 함수: 두 문자열이 같다면 0 반환
-- ↪ 양수를 반환한다면 첫번째 문자열이 큰 경우이고 음수를 반환한다면 작은 경우 (알파벳 기준)
-- ↪ # include string.h 필요
- typedef : 새로운 타입을 정의 (나만의 자료형 만들기)
-- ⨁ struct (구조체) : 그릇처럼 여러가지 자료형을 담을 수 있음
typedef struct { string name; string number; } person;중괄호로 감싸져 있는 것을 캡슐화 라고 하며 마지막에 person 은 구조체의 이름(별칭) 이다.
4. 버블 정렬
- 학습목표: 버블 정렬의 원리와 실행시간을 설명하고 구현할 수 있다.
- 핵심단어: 버블정렬
1) Big O : O (n²)
-- 선형 및 이진 검색보다 상한선이 높음
(n-1) ⨯ (n-1)
n² - 1n - 1n + 1
n² -2n + 1
⨁ 이진 검색이 선형 검색보다 상한선이 낮지만, 이진 검색을 위한 조건이 정렬인 것을 생각해보면 이진 검색이 선형 검색보다 반드시 좋다고 할 수는 없다는 것을 알 수 있다.
2) Big Ω : Ω (n²)
-- 이미 정렬된 배열이더라도 작동하므로 하한선 역시 제곱이다. (최적화 기법이 없을 때)
5. 선택정렬
- 학습목표: 선택정렬의 원리와 실행시간을 설명 및 구현할 수 있다.
- 핵심단어: 선택정렬
1) Big O : O (n²)
-- 버블정렬과는 근본적으로 다른 알고리즘이지만, 수학적 혹은 실제로는 같은 성능을 가짐
n + (n-1) + (n-2) + … + 1
n(n+1) / 2
(n²+n) / 2
n²/2 + n/2
2) Big Ω : Ω (n²)
-- 버블정렬과 같은 의미로 최선의 경우에도 시간이 똑같이 소요됨
6. 정렬 알고리즘의 실행시간
- 학습목표: 여러 정렬 및 검색 알고리즘의 실행시간을 Big O, Big Ω 로 정의할 수 있다.
- 핵심단어: Big O, Big Ω
-- 교환이 없을 때 알고리즘을 일찍 종료한다면 최선의 경우에 n-1 번의 과정이 필요 ⇒ Ω (n²) → Ω (n)
7. 재귀 (Recursion)
- 학습목표: 함수를 재귀적으로 사용하는 코드를 작성할 수 있다.
- 핵심단어: 재귀
- 눈에 보보는 혹은 가상의 물체의 구조를 그 물체 자체를 이용하여 설명하는 것
ex) 슈퍼마리오에 있는 피라미드
↪ 높이 4 피라미드에서 하나씩 줄일 때 마지막 부분에서 반환 or 종료 or 정지 등 알고리즘에 맞게 처리가 필요
- 스스로 호출하면서 기존 문제보다 더 작은 크기의 문제를 풀어감 (like 이진탐색, 분할 정복법)
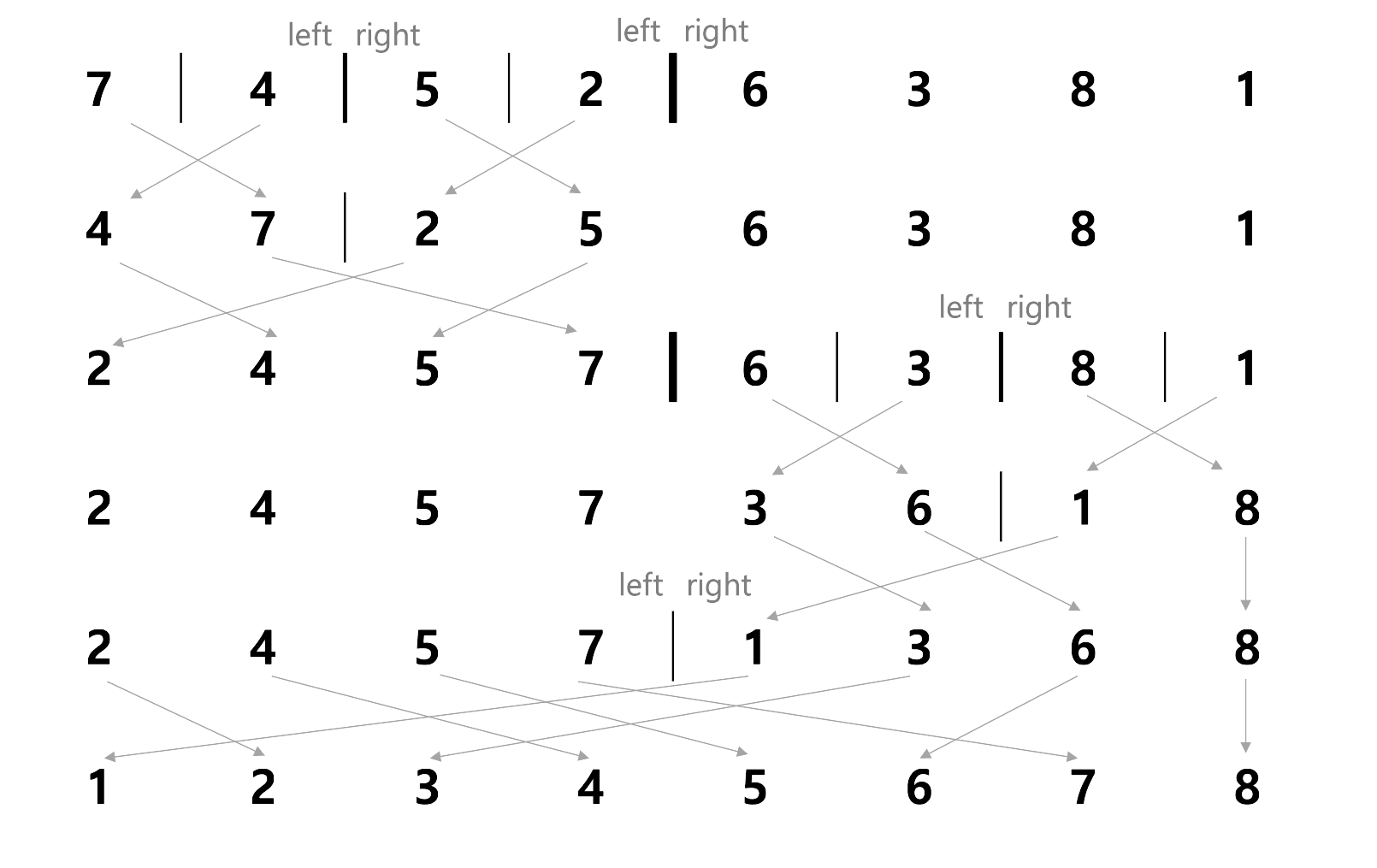
8. 병합 정렬
- 학습목표: 재귀를 활용한 병합 정렬을 구현할 수 있다.
- 핵심단어: 병합정렬
1) 재귀 알고리즘의 핵심
-- 왼쪽~오른쪽, 병합(else), return (if item==one)
ex) 두 배열 중 가장 작은 값을 꺼내 다른 배열의 가장 작은 값의 다음에 두는 과정
2) 병합정렬의 실행시간: n ⨯ log n
-- 크기 8인 배열을 쪼개서 크기 1인 배열 8개로 만드는데 필요한 과정으로 약 log n, 그 후 n개의 숫자를 다시 합치는 과정을 n번 반복
⨁ Theta 표기법: 어떤 알고리즘의 상한선과 하한선이 같을 때
| theta (θ) | |
|---|---|
| θ (n²) | selection sort |
| ———— | —————— |
| θ (n log n) | merge sort |
| ———— | —————— |
| θ (n) | - |
| ———— | —————— |
| θ (log n) | - |
| ———— | —————— |
| θ (1) | - |
-- ↪ 선택정렬 및 병합정렬은 맹목적으로 같은 알고리즘을 계속 반복하므로 상한선과 하한선이 같음