Euler Method와 Graph Plot

What is Euler Method?

오일러(Euler)법은 미분방정식을 푸는 방법 중 하나이다.
-> 초기값과 i번째 1차 도함수의 기울기를 이용하여 i+1번째 함수값을 예측하기 위한 방법이라고 볼 수 있다.

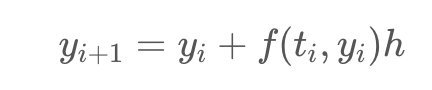
//오일러 함수 설정하기
function [t,y] = MyEuler(f, tinterval, y0, n)
    y = zeros(n+1,1);
    y(1) = y0 
    dt = (tinterval(2) - tinterval(1))/n; 
    t = tinterval(1):dt:tinterval(2); 
    for i = 1:n
        y(i+1) = y(i) + f(t(i),y(i))*dt
    end
    t = t';
endfunction

• zeros(n,m): 행,열 영벡터 생성
• t = tinterval(1):dt:tinterval(2) : dt의 크기만큼 중간을 나눠서 벡터 생성

오일러함수로 근사한 함수와 Exact함수 plot하기

• 실제 해는 Maple에서 답을 찾아 구해서 Exact함수를 지정한다.
• Euler함수는 기본적인 Approximation이기 때문에 이를 따로 Plot 해준다.

function yp = DE(t,y)
    yp = (t.^3 - t.^2-7*t-5)*exp(t)
endfunction

function y = exact(t)
    //y = (t^3-4*t^2+t-6)*exp(t) + 6
    y = (-6+t-4*t.^2+t.^3)*exp(t)+6
endfunction

[t,y] = MyEuler(DE, [0,4], 0, 10);
[t1,y1] = MyEuler(DE, [0,4], 0, 20);
[t2,y2] = MyEuler(DE, [0,4], 0, 40);

scf(0);
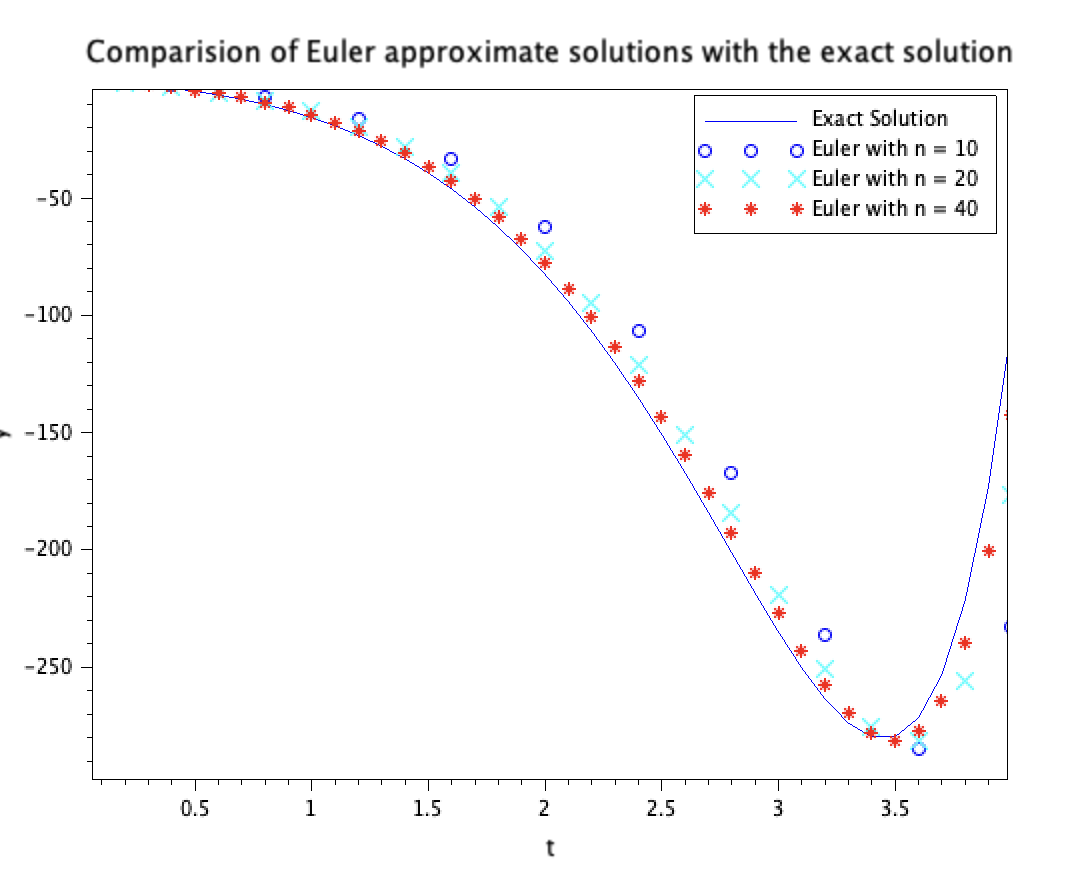
plot(0:0.1: 4, exact);
plot(t, y,'bo', t1, y1, 'cx', t2, y2, 'r*');
legend('Exact Solution','Euler with n = 10','Euler with n = 20','Euler with n = 40')
xtitle('Comparision of Euler approximate solutions with the exact solution', 't', 'y');

• yp : 1계도함수 Differential Equation -> 한번 미분한 원래 주어진 함수를 뜻함
• y(Exact) : 주어진 함수의 원함수를 뜻함, Maple 이용해서 실제해를 구한다.
• Plot(x값, y값, 색상/마킹,...) : 함수를 거쳐서 나온 t값 벡터와 y값 벡터를 넣고, 해당 값들을 지정할 색상 마킹을 지정해주면,이를 한 세트로 그래프가 그려짐
• legend: 그려지는 그래프를 순서대로 범례를 작성해줌
• xtitle: 타이틀, x값단위, y값 단위.

결과값