힙 / 힙 큐

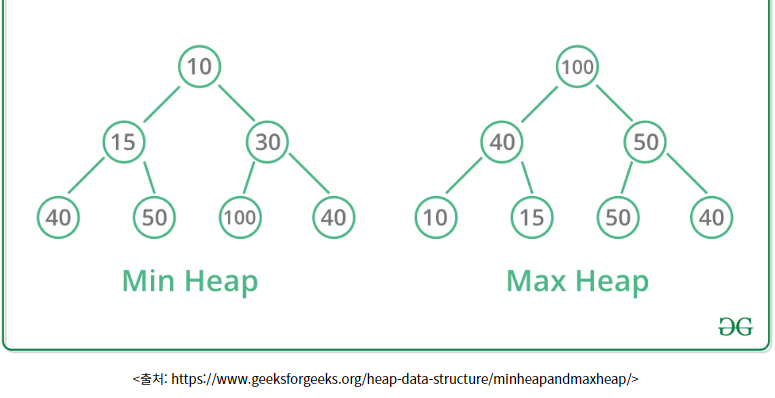
1. 힙: 특정한 규칙을 가지는 트리. 최댓값과 최솟값을 찾는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 함.

2. 최소 힙: 부모 노드의 키값이 자식 노드의 키값보다 항상 작은 힙 / 루트 노드에 최솟값이 있는 것

3. 최대 힙: 부모 노드의 키값이 자식 노드의 키값보다 항상 큰 힙 / 루트 노드에 최댓값이 있는 것

+ 힙의 루트노드는 0번 인덱스이다!!!!!!

4. heapq(힙큐): 파이썬에서, 리스트를 최소 힙처럼 다룰수 있도록 하는 모듈. 파이썬의 heapq에서는 최소힙을(최소힙만) 제공된다.

---

- 힙 함수

1. heapq.heappush(heap, item) : item을 heap에 추가
2. heapq.heappop(heap) : heap에서 가장 작은 원소를 pop & 리턴. 비어 있는 경우 IndexError가 호출됨.
3. heapq.heapify(x) : 리스트 x를 즉각적으로 heap으로 변환함 (in linear time, O(N))

---

이를 활용한 문제

from heapq import * # heapq 에 있는 것을 전부(*) 가져온다. 
# heapq: 리스트를 최소 힙처럼 다룰수 있도록 하는 모듈
# 최소 힙: 부모 노드의 키값이 자식 노드의 키값보다 항상 작은 힙 / 루트 노드에 최솟값이 있는 것
def solution(scoville, K):
    count = 0 
    heapify(scoville) # 힙함수 heapify. 인자로 받은 리스트를 즉각적으로 heap으로 변환함. 여기서 scoville은 최소힙이 되는 것이다.
    while scoville[0] < K and len(scoville) > 1:  # 가장 맵지 않은 스코빌 지수가 K보다 작고 스코빌 길이가 1보다 길때
        num1 = heappop(scoville) # 힙함수 heappop. heap에서 가장 작은 원소를 pop & return
        num2 = heappop(scoville)
        heappush(scoville, num1 + num2 * 2) # heappush(heap, item). item을 heap에 추가
        count += 1
    return count if scoville[0] >= K else -1 
# 반복문 while이 끝난다는 것은 스코빌의 길이가 1이 되거나, 가장 맵지 않은 스코빌 지수가 K 이상이 되었다는 것이다. (둘 중 하나)
# 물론 스코빌 길이가 1이면서 가장 맵지 않은 스코빌 지수가 K 이상이 될 수도 있다. (둘 다)
# 뭐가 되었든(둘 중 하나만이든 둘 다이든) 가장 맵지 않은 스코빌 지수가 K이상이 되었다면, 성공했다는 뜻이므로 누적된 count를 그대로 반환하면 된다.
# 그렇지 않은 경우, 즉 스코빌의 길이가 1이 되었는데 가장 맵지 않은 스코빌 지수가 K보다 작다면, -1을 반환한다.
# 리턴문을 위처럼 한 줄로 반환할 수도 있다. 

• (중요) 힙의 루트 노드는 0번 인덱스이다. 그렇다면, 최소 힙에서, 0번 인덱스에 최소값이 존재하는 것이다(최대 힙에서는 0번 인덱스에 최댓값이 존재).
• (중요) 앞서 말했듯이, 파이썬의 힙큐에서는 최소힙만 제공되므로, 위문제에서처럼 파이썬에서 힙큐를 가져와 heapify를 사용하면, 리스트가 최소힙으로 변환된다.
• (중요) 다시 한 번 말하지만, 힙큐는 파이썬에서 리스트를 최소힙처럼 다룰 수 있도록 하는 모듈이다.

참고: https://littlefoxdiary.tistory.com/3
참고: https://latte-is-horse.tistory.com/137