문제 해설

유클리드 호재법에 관한 문제이다.

나는 일단 이런 부분은 몰랐기 떄문에 재귀로 해결을 하려고 하엿다.

• 재귀로 부분 집합을 표현할수 있기 떄문에

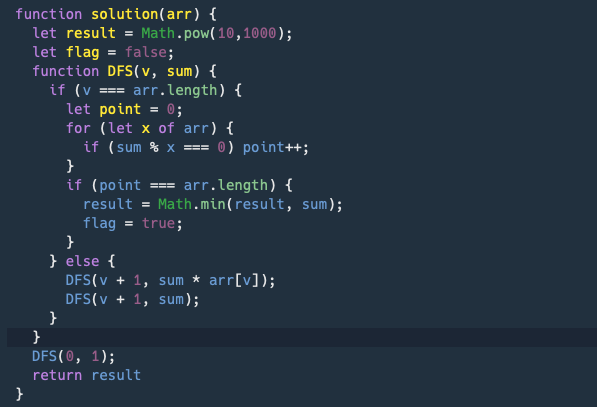
• 내가 짠 코드이다.

결과적으로는 테스트를 통과 하지 못했다..

• flag는 필요가 없다 깜빡하고 지우지 못했다.

부분 집합으로 들어오는 값을 모두 곱하면서 비교를 하였다.

재귀가 if문을 타게 되면 들어오는 sum값을 비교해 point를 쌓고

point가 length값이 된다는 조건은 모두 통과 하였다는 조건이기 떄문에

만약 그렇다면 최소값을 배정하는 식으로 문제를 해결을 하였다.

하지만 통과를 하지 못했다.... ㅠㅠ

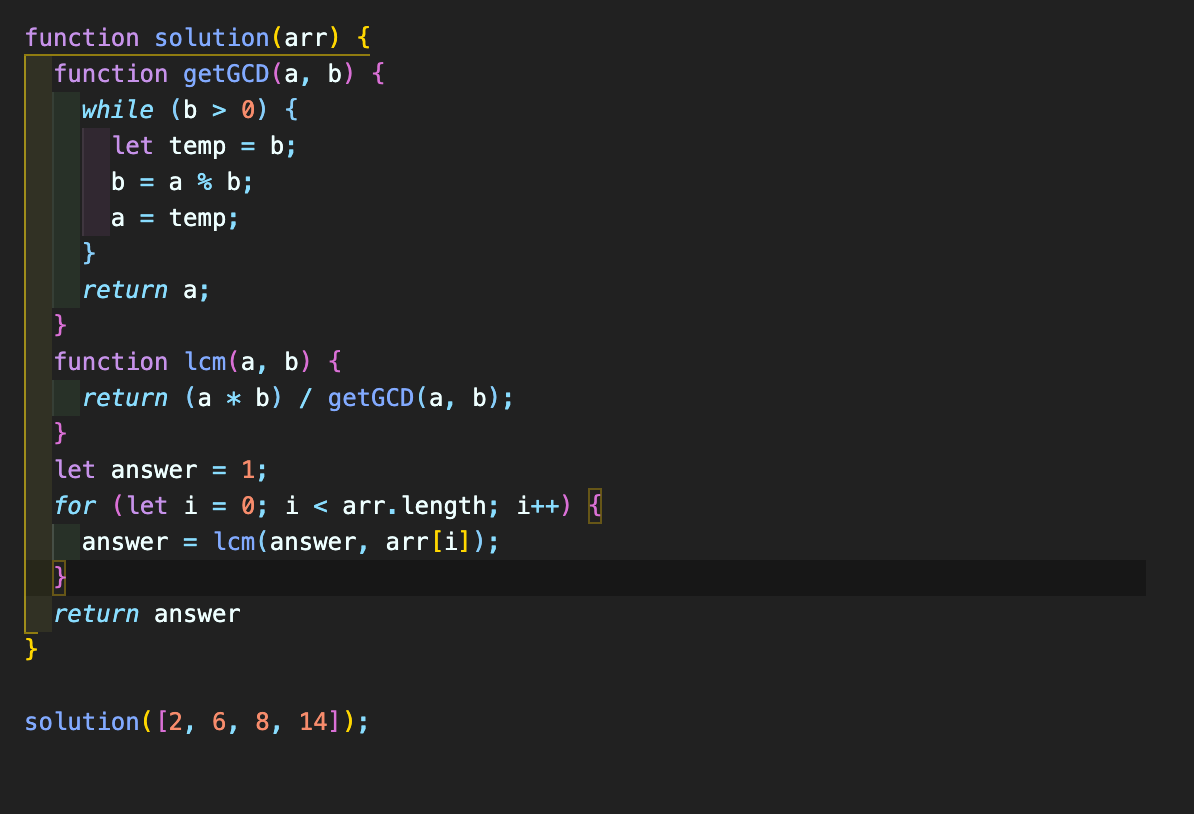
• 인터넷을 뒤적거려서 찾은 코드이다.

유클리드 호제법이라는 것을 활용을 하였다고 한다.

• 일단 난 몰랐으며 알았어도... 가능했으려나??

getGCD : 최대 공약수를 구하는 곳이다.
lcm : 최대 공배수를 구하는 곳이다.

유클리드 호제법

출처 : https://velog.io/@yerin4847/W1-유클리드-호제법

두 수의 최대공약수를 구하는 알고리즘이다.

보통 소인수 분해를 하게 되면 구할수 있지만 값이 커지게 되면 어려워 진다는 단점이 있다.

이떄 활용하는 방법이다!!

일단 MOD연산에 대해서 알고 있어야 하는데

• 두 값을 나눈 나머지를 구하는 연산

나머지를 구하는 이 연산을 계속 하면서 나머지가 0이 되었을떄를 찾는다.

• 나머지가 0 이 될떄 나누는 값이 바로 최대 공약수 이다.

1112 mod 695 = 417
695 mod 417 = 278
417 % 278 = 139
278 % 139 = 0

이떄 139가 최대 공약수 이다.