깊이 우선 탐색(DFS)

1) 구현 방법

인접 행렬: 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식이다. 모든 관계를 저장하므로 노드 개수가 많을수록 메모리가 불필요하게 낭비된다.

인접 리스트: 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장한다. 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용한다. 하지만 연결된 데이터를 하나씩 확인해야 하기에 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다.

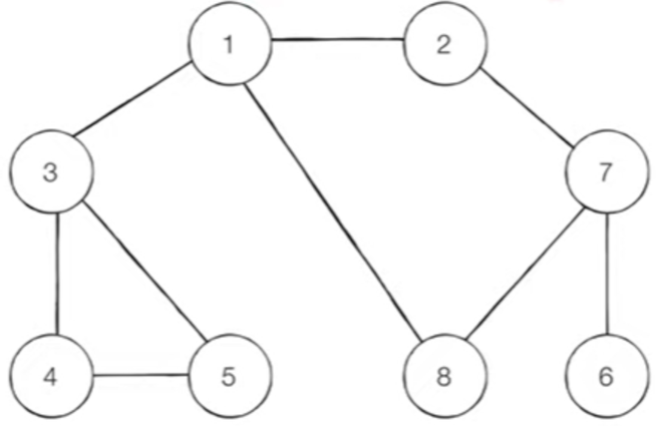
위 그래프에 대한 리스트를 다음과 같이 표현할 수 있다.

graph = [
    [],
    [2,3,8],
    [1,7],
    [1,4,5],
    [3,5],
    [3,4],
    [7],
    [2,6,8],
    [1,7]
]

2) 구현

#인접 행렬
n, m, v = map(int, input().split())
graph = [[False] * (n+1) for _ in range(n+1)]

for i in range(m):
    x,y = map(int, input().split())
    graph[x][y] = 1
    graph[y][x] = 1

visited = [False] * (n+1)

def dfs(v):
    visited[v] = True
    print(v, end=' ')
    for i in range(1, n+1):
        if not visited[i] and graph[i][v] == 1:
            dfs(i)
            
dfs(v)

#인접 리스트
n,m,v = map(int, input().split())
graph = [[] for _ in range(n+1)]

for _ in range(m):
    x,y = map(int, input().split())
    graph[x].append(y)
    graph[y].append(x)
    
for x in graph:
    x.sort()

visited = [False] * (n+1)

def dfs(v):
    visited[v] = True
    print(v, end=' ')
    for i in graph[v]:
        if not visited[i]:
            dfs(i)            
dfs(v)