백준-트리

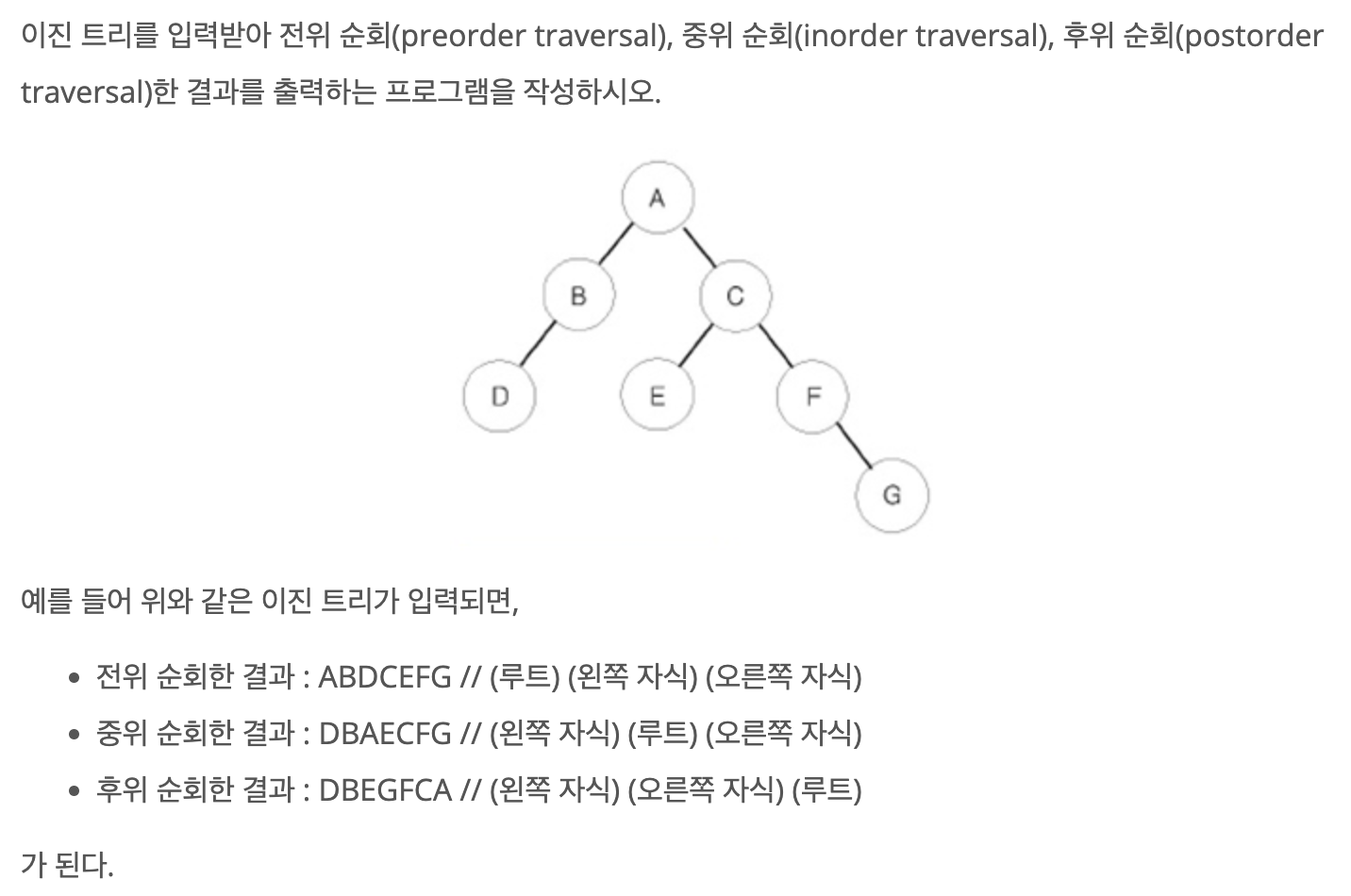
1. 문제

2. 해결

import sys
input = sys.stdin.readline

def preorder(Tree, data):
    print(data, end='')

    if Tree[data][0] != '.':
        preorder(Tree, Tree[data][0])

    if Tree[data][1] != '.':
        preorder(Tree, Tree[data][1])

    return

def inorder(Tree, data):
    if Tree[data][0] != '.':
        inorder(Tree, Tree[data][0])
    
    print(data, end='')

    if Tree[data][1] != '.':
        inorder(Tree, Tree[data][1])
    
    return

def postorder(Tree, data):
    if Tree[data][0] != '.':
        postorder(Tree, Tree[data][0])

    if Tree[data][1] != '.':
        postorder(Tree, Tree[data][1])

    print(data, end='')

    return

def solution(n):
    Tree = dict()

    for i in range(n):
        root, left, right = input().split()
        Tree[root] = [left, right]

    preorder(Tree, 'A')
    print()

    inorder(Tree, 'A')
    print()

    postorder(Tree, 'A')
    print()

solution(int(input()))

3. 풀이

1) 순회 함수들

• 'Tree'는 트리 구조를 저장하는 딕셔너리이며, 'Tree[data][0]'은 data 노드의 왼쪽 자식을, Tree[data][1]은 data 노드의 오른쪽 자식을 나타낸다.

Tree = {
    'A': ['B', 'C'],
    'B': ['D', '.'],
    'C': ['E', 'F'],
    'D': ['.', '.'],
    'E': ['.', '.'],
    'F': ['.', 'G'],
    'G': ['.', '.']
}

-> 위 코드에서 A 노드의 왼쪽 자식은 B, 오른쪽 자식은 C이다.

• . 은 해당 자식 노드가 없음을 의미한다.

2) solution 함수

• solution(n): 노드의 개수를 인수로 받아 트리를 구성하고, 순회 결과를 출력한다.
• Tree[root] = [left, right]: 딕셔너리에 루트를 key로, 왼쪽 자식과 오른쪽 자식을 value로 저장한다.