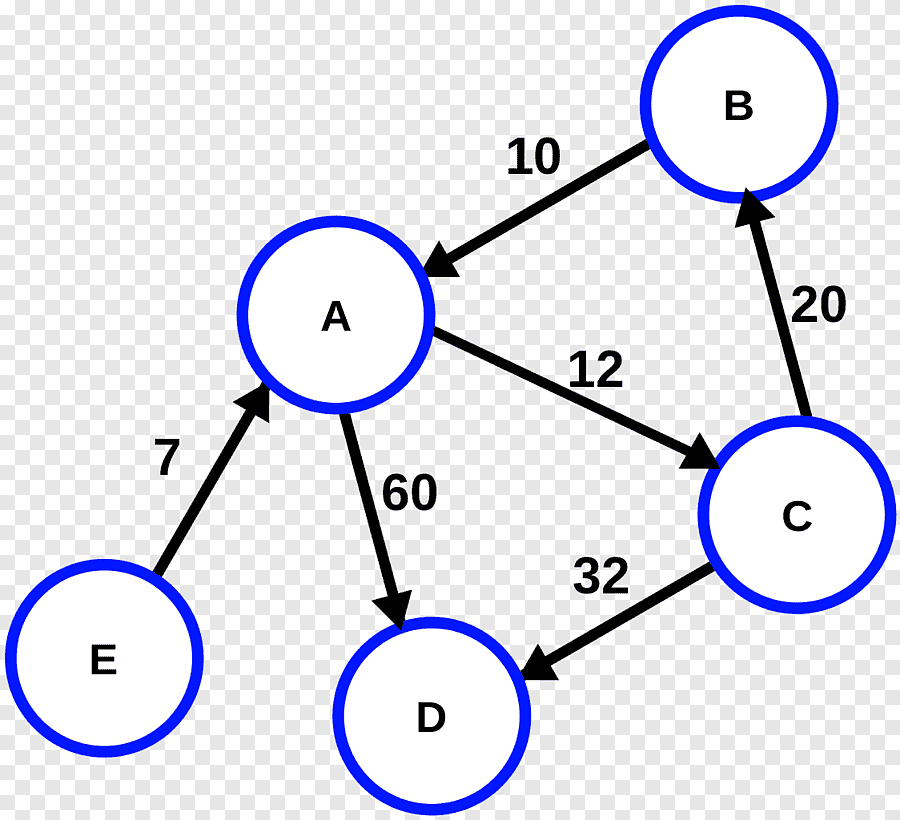
🌟다익스트라 vs 플로이드-워셜

• 그림 필요

🎇 다익스트라

1. 정의

하나의 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로 구하는 알고리즘

---

2. 특징

조건 : 양의 가중치에서는 상관 없지만, 음의 가중치에서는 사이클이 있을 때 무한 루프에 빠지기 때문에 사용 X -> [플로이드-워셜] 사용

• 노드와 간선 필요
• 3개의 변수 지정 필요 : Graph, Distance, Heapq에 들어갈 리스트 q
• 시간 복잡도 : E * log(V)
• BFS, 그리디 알고리즘 계열

---

3.1. 기본 예시

import sys
import heapq 
input = sys.stdin.readline

N, M = map(int, input().split())
graph = [[] for _ in range(N+1)]
INF = int(1e9)

# 1. 비용과 함께 그래프 노드 포함한 이중 리스트 Setting
for i in range(M):
    a, b, cow = map(int, input().split())
    graph[a].append((cow, b))
    graph[b].append((cow, a))

def dijkstra(S):    
    Q = []
    distance = [INF] * (N+1)
    # 2. 다익스트라 함수 내에 Heapq 모듈의 heappush 함수활용하여 힙 리스트 init
    heapq.heappush(Q, (0, S))
    distance[S] = 0
    # 3. 반복문을 활용하여 heappop 함수 활용하여 Distance 리스트의 거리를 Update
    while Q:
        now_dist, now_vertex = heapq.heappop(Q)
        # 가지치기 함 해주고
        if now_dist > distance[now_vertex]:
            continue
        # 애초에 설정된 거리와 a, b 거리 비교해서 a+b 크기가 작으면 이걸로 distance 갱신해줌
        for next_dist, next_vertex in graph[now_vertex]:
            if now_dist + next_dist < distance[next_vertex]:
                distance[next_vertex] = now_dist + next_dist
                heapq.heappush(Q, (now_dist + next_dist, next_vertex))
    
    return distance
# 4. 출발지 입력하여 거리 계산
print(dijkstra(1)[N])

3.2. Graph 이론 + Dijkstra - 네트워크 복구

• Parent 이용 : [Graph이론]

import sys
import heapq
input = sys.stdin.readline
INF = int(1e9)

def dijkstra(start):
    q = []
    distance[start] = 0
    heapq.heappush(q, (0, start))
    
    while q:
        dist, now = heapq.heappop(q)
        
        if distance[now] < dist:
            continue
        
        for next_node, next_cost in graph[now]:
            cost = dist + next_cost
            
            if distance[next_node] > cost:
                # 더 짧은 거리로 갱신될 때마다 parent도 함께 갱신
                parent[next_node] = now
                distance[next_node] = cost
                heapq.heappush(q, (cost, next_node))
                
n, m = map(int, input().split())

distance = [INF] * (n+1)
parent = [0] * (n+1)
graph = [[] for _ in range(n+1)]

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))
    graph[b].append((a, c))
    
dijkstra(1)

print(n-1)
for i in range(2, n + 1):
    print(i, parent[i])

---

🎇 플로이드-워셜

---

1. 정의

모든 정점에서 다른 모든 정점으로의 최단 경로 구하는 알고리즘

---

2. 특징

• Node 개수 500개 이하일 때만 사용