🌟트리

1. 루트 (ROOT) : 최상위 노드로, 부모 노드가 없이 자식 노드만 가질 수 있다.
2. 리프 노드 (Leaf Node) : 최말단 노드

🎇 완전 이진트리

1. 루트(Root)부터 아래쪽 레벨(Lv)로 가득 차 있음
2. 마지막 레벨(Lv)에서 왼쪽부터 오른쪽으로 노드가 차 있음

🎇 이진 탐색트리(BST - Binary Search Tree)

• 정의

모든 노드의 차수가 2 이하인 트리

• 아래의 조건을 만족해야 함

1. 왼쪽 서브트리 노드의 키는 자신의 노드 키보다 작아야 한다 ( 왼쪽 < 자신)
2. 오른쪽 서브트리 노드의 키는 자신의 노드 키보다 커야 한다 ( 오른쪽 > 자신)
3. 키가 같은 노드는 복수로 존재하지 않는다!

• 여기서 잠깐 서브트리란? (작은 트리)

하나의 트리를 구성하는 왼쪽과 오른쪽의 작은 트리를 가리킴 !

• 숫자를 이진 수로 만드는 과정

  숫자를 계속해서 2로 나누면서 나머지를 저장하고, 그 나머지들을 뒤집으면 이진수 완성 !!

---

🧨 표현 가능한 이진 트리 - 프로그래머스 Lv3

def makeBinaryNumber(number):
    reverseBinaryNumber = []
    # 이진수로 만듦
    while number != 1:
        reverseBinaryNumber.append(str(number % 2))
        number //= 2
    reverseBinaryNumber.append("1")
    binaryNumber = ''.join(reverseBinaryNumber[::-1])
    
    binaryTreeSize = 1
    while binaryTreeSize < len(binaryNumber):
        binaryTreeSize = (binaryTreeSize + 1) * 2 - 1
    binaryNumber = "0" * (binaryTreeSize - len(binaryNumber)) + binaryNumber
    return binaryNumber



def checkPossible(start, end, binaryString):
    if start == end:
        return binaryString[start]
    mid = (start + end) // 2
    # 왼쪽 재귀로 탐색
    left = checkPossible(start, mid-1, binaryString)
    # Case1 에러 [Mid = 0 일시] 0-1-0, 1-0-0
    if not left or (binaryString[mid] == "0" and left == "1"):
        return False
    # 오른쪽 재귀로 탐색
    right = checkPossible(mid + 1, end, binaryString)
    # Case2 에러 [Mid = 0 일시]
    if not right or (binaryString[mid] == "0" and right == "1"):
        return False
    # Case3 에러 [Mid = 0 일시]
    # Left, Mid, Right : 0-0-0 총 3가지 경우의 수 (mid = '0'일 시 문제)
    if left == "0" and right == "0" and binaryString[mid] == "0":
        return "0"
    
    return "1"




def solution(numbers):
    answer = []
    for number in numbers:
        binaryNumber = makeBinaryNumber(number)
        if checkPossible(0, len(binaryNumber)-1, binaryNumber):
            answer.append(1)
        else:
            answer.append(0)
    return answer

---

🌟 그래프

🧨 그래프 정의

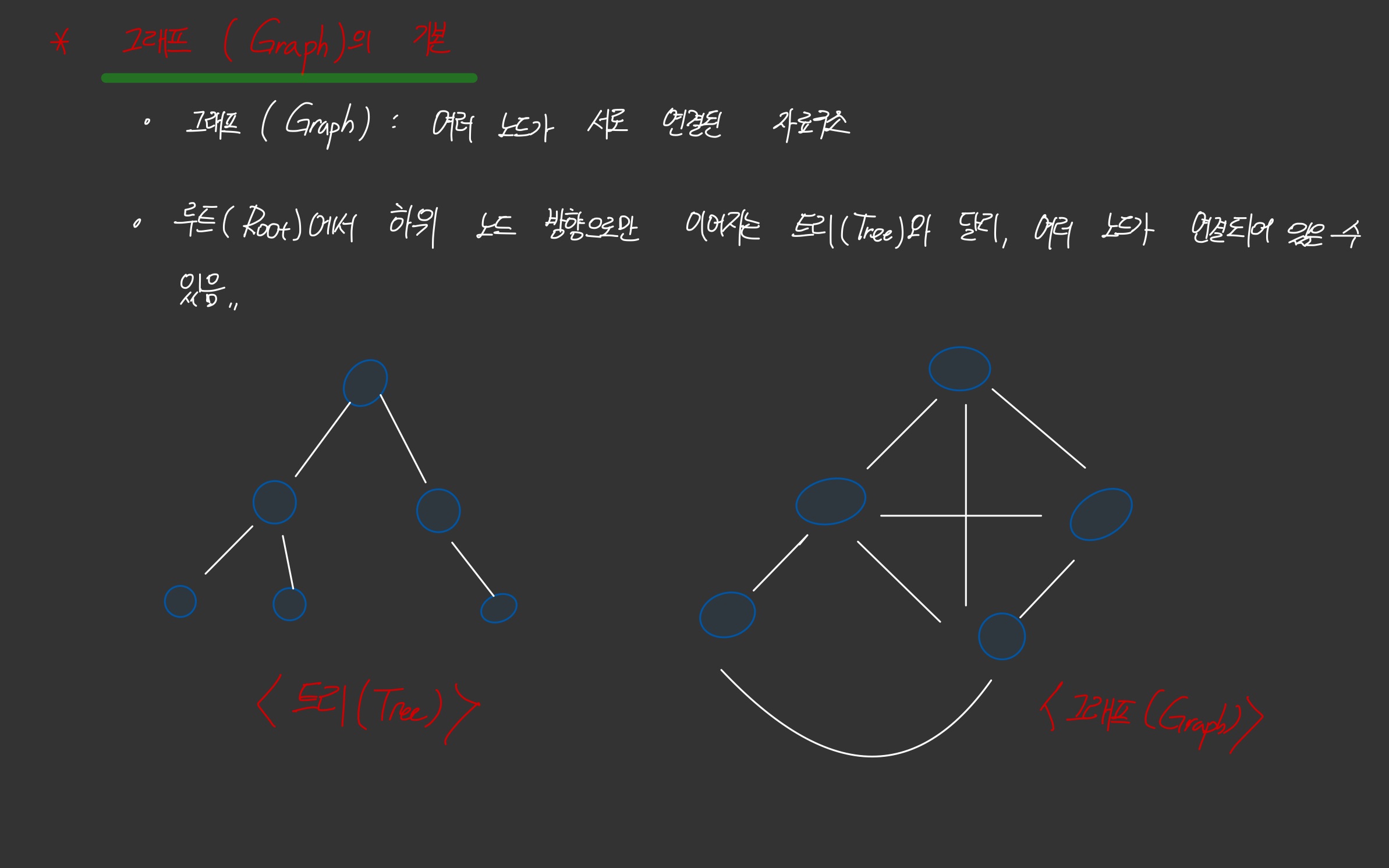
• 트리 VS 그래프

1. 트리 : 루트에서 하위 노드방향으로만 이어져
2. 그래프 : 여러 노드(Vertex)가 서로 연결된 자료구조

🧨 그래프 종류

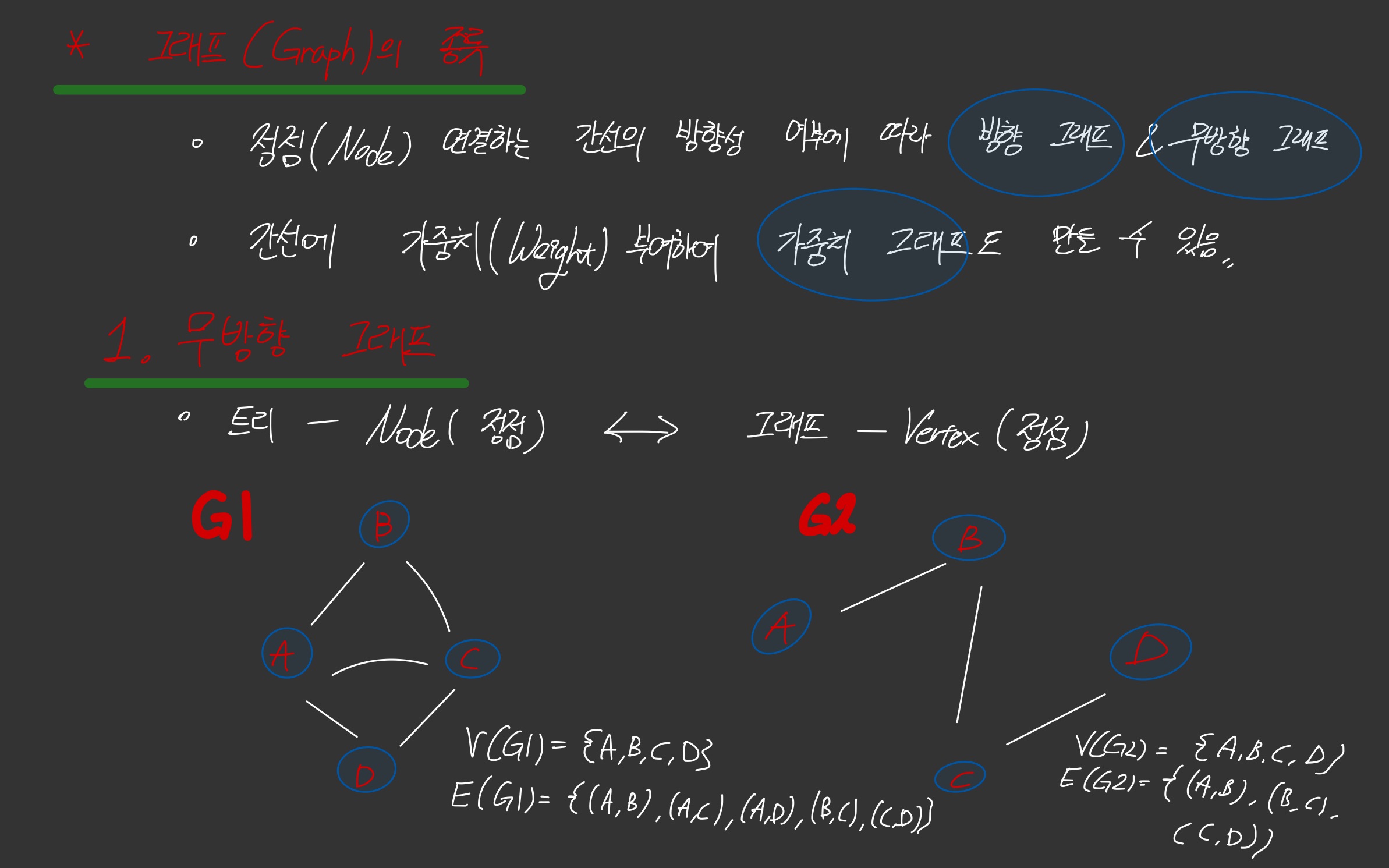
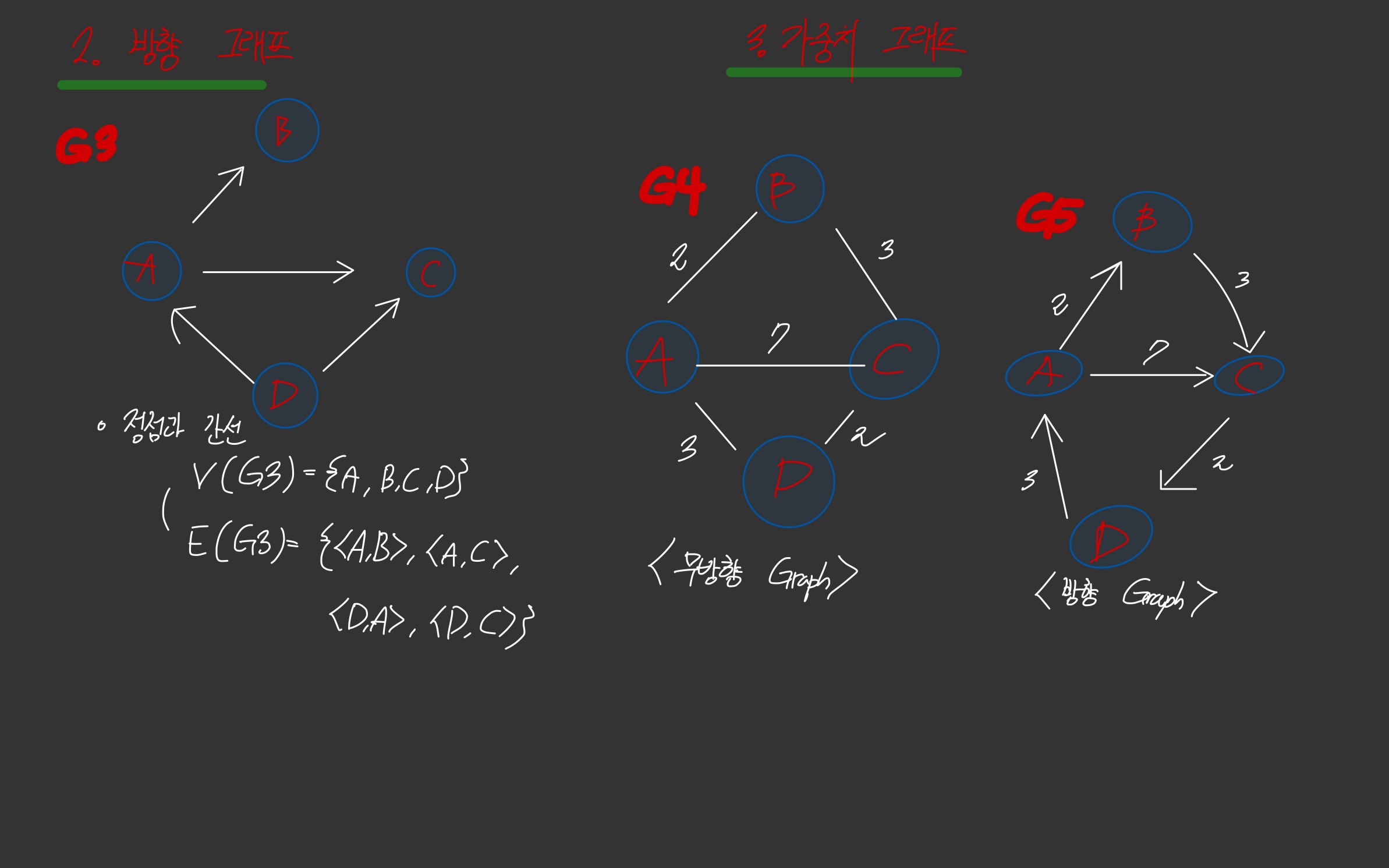
1. 무방향 그래프
2. 방향 그래프
3. 가중치 그래프

---

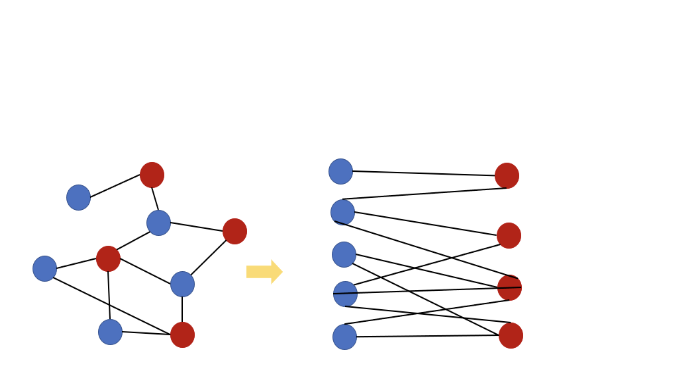
🎇 이분 그래프란?

• 각 노드, 정점에 대해서 해당 정점과 연결된 정점들이 모두 다른 색깔이어야 돼 ! (즉, 다른 그룹이어야 됌)
• BFS, DFS 탐색 이용해서 확인하면 됌! - 시간복잡도는 모든 정점을 방문하면서 간선 검사하기 때문에 O(V+E)

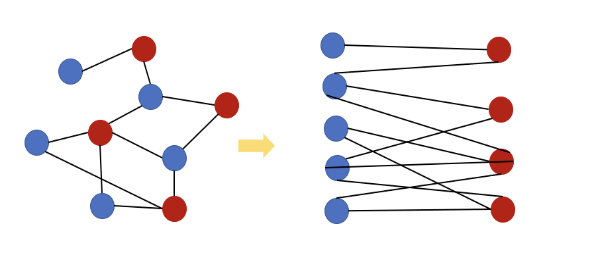
[출처 : https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html]

---

🧨 백준 - 이분 그래프 문제[DFS 활용]

import sys

sys.setrecursionlimit(20000)
input = sys.stdin.readline

def dfs(start, group):
    global error 
    
    if error:
        return
    
    visited[start] = group
    
    for i in graph[start]:
        if not visited[i]:
            dfs(i, -group)
        elif visited[start] == visited[i]:
            error = True
            return

T = int(input())

for _ in range(T):
    V, E = map(int, input().split())
    graph = [[] for _ in range(V + 1)]
    visited = [False] * (V + 1)
    error = False
    
    for _ in range(E):
        a, b = map(int, input().split())
        graph[a].append(b)
        graph[b].append(a)
        
    for i in range(1, V + 1):
        if not visited[i]:
            dfs(i, 1)
            if error:
                break
            
    print('NO' if error else 'YES')

---

🎇 활용

이분 그래프(bipartite graph)는 그래프 이론에서 매우 중요한 개념 중 하나 ! 이분 그래프는 정점을 두 개의 그룹으로 분할한 후, 각 그룹 내의 정점끼리는 연결되지 않고, 반대 그룹의 정점들과만 연결된 그래프~~

이분 그래프는 다양한 분야에서 활용돼~~
몇 가지 예를 들어보면:

1. 매칭 문제: 이분 그래프에서 각 그룹의 정점들 중에서 하나의 정점만 선택하고, 서로 연결되어 있는 정점끼리 매칭시키는 문제입니다. 이분 그래프를 이용하여 매칭 문제를 해결할 수 있습니다.
2. 네트워크 흐름 문제: 이분 그래프를 이용하여 최대 유량(maximum flow) 문제를 해결할 수 있습니다.
3. 통신 네트워크: 이분 그래프를 이용하여 통신 네트워크에서 서로 다른 그룹의 정점들끼리 연결되도록 라우팅(routing)을 구성할 수 있습니다.
4. 소셜 네트워크 분석: 이분 그래프를 이용하여 소셜 네트워크에서 친구 관계를 분석하고, 각 그룹의 특성을 파악할 수 있습니다.