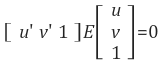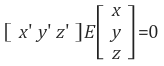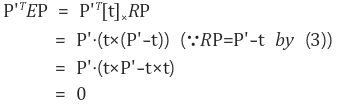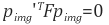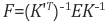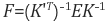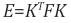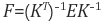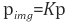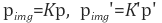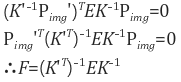Camera Calibration
카메라의 파라미터(parameters)를 추정하는 과정을 카메라 캘리브레이션이라고 한다.
실세계의 3D 점과 캘리브레이션된 카메라로 캡처한 이미지의 해당 2D 투영(픽셀)간의 정확한 관계를 결정하는데 필요한, 카메라에 대한 모든 정보(파라미터 또는 계수)를 의한다.
일반적으로 이것은 두 종류의 파라미터를 복구하는 것을 의미한다.
-
카메라/렌즈 시스템의 내부 파라미터(Internal parameters): 초점 거리(focal length), 광학 중심(optical center), 렌즈의 방사 왜곡 계수(radial distortion coefficients of the lens).
-
외부 파라미터(External parameters): 이것은 일부 세계 좌표계에 대한 카메라의 방향(회전 및 이동, Rotation and translation)을 나타냅니다.
첫 번째 게시물인, Camera Calibration 게시물에서 Camera Calibration을 계산하고 카메라에 내부 파라미터(Intrinsic Parameter)을 구하는 방법에 대해 학습하였다.
[https://velog.io/@jjun-ho/Iron-View-1-Image-Stiching]
Self-Calibration
Self-calibration refers to the process of calculating all the intrinsic parameters of the camera using only the information available in the images taken by that camera. No calibration frame or known object is needed: the only requirement is that there is a static object in the scene, and the camera moves around taking images. Thus self-calibration is ideal for a mobile camera, such as a camera mounted on a mobile robot.
Self-calibration 은 카메라가 촬영한 이미지에서 사용할 수 있는 정보만을 사용하여 카메라의 모든 고유 매개 변수를 계산하는 과정을 말합니다.
일반적으로 알고있는 camera calibration이 카메라 보정을 위한 격자나 보정판이 필요하다면 self-calibration은 이런 것 없이 카메라 보정을 할 수 있는 방법이다.
단지 영상에서 특징점을 추출하여 fundamental matrix를 구하여 카메라 보정을 하는 방법(fundamental matrix를 계산하면 epipole, projective space에서의 camera matrix, essential matrix를 계산할 수 있다)인데 유클리디안 공간으로 업데이트 하는데 어려움이 있겠지만 유용한 방법인 것 같다.
Self-calibration를 Epipolar Geometry의 개념을 알아야한다.
Epipolar Geometry 개념은 '다크 프로그래머'님의 [영상 Geometry #7] Epipolar Geometry 게시물을 참고하였습니다.
Epipolar Geometry
Epipolar geometry는 동일한 사물 또는 장면에 대한 영상을 서로 다른 두 지점에서 획득했을 때, 영상 A와 영상 B의 매칭쌍들 사이의 기하학적 관계를 다루는 것이다.
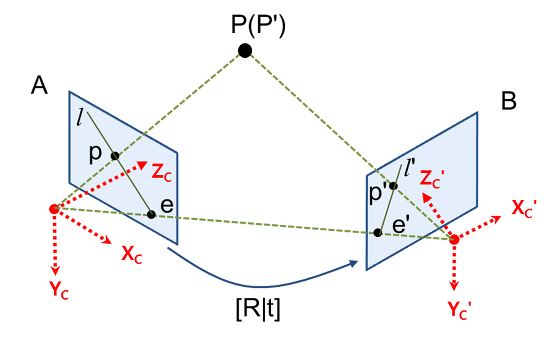
용어 및 기본 개념
3차원 공간상의 한 점 P가 영상 A에서는 p에 투영되고, 영상 B에서는 p'에 투영됐다고 하겠습니다. 이 때, 두 카메라 원점을 잇는 선과 이미지 평면이 만나는 점 e, e'을 epipole이라 부르고 투영점과 epipole을 잇는 직선 l, l'을 epiline (또는 epipolar line)이라 부릅니다. Epiline은 3차원의 점 P와 두 카메라 원점을 잇는 평면(epipolar plane)과 이미지 평면과의 교선으로도 볼 수 있습니다.
두 카메라 위치 사이의 기하학적 관계 [R|t]를 알고 있고 영상 A에서의 영상좌표 p를 알고 있을 때, 영상 B에서 대응되는 점 p'의 좌표를 구하는 문제를 생각해 보겠습니다. 이 때, 점 P까지의 거리(depth) 정보를 모른다면 영상좌표 p로부터 투영되기 전의 3차원 좌표 P를 복원할 수는 없습니다. 따라서 점 P가 영상 B에 투영된 좌표 p' 또한 유일하게 결정할 수 없습니다. 하지만 점 P는 A 카메라의 원점과 p를 잇는 직선(ray) 상에 존재하기 때문에 이 직선을 영상 B에 투영시키면 점 p'이 이 투영된 직선 위에 있음은 알 수 있습니다. 이 투영된 직선이 바로 epiline l' 입니다.
정리하면, A의 영상좌표 p로부터 대응되는 B의 영상좌표 p'을 유일하게 결정할 수는 없지만 p'이 지나는 직선인 epiline l'은 유일하게 결정할수 있다' 입니다. 그리고 한 영상좌표로부터 다른 영상에서의 대응되는 epiline을 계산해주는 변환행렬이 Fundamental Matrix, Essential Matrix 입니다. 즉, 서로 다른 두 시점에서 찍은 영상좌표들 사이에는 Fundamental Matrix, Essential Matrix를 매개로 하는 어떤 변환 관계가 성립하는데, Epipolar Geometry에서는 이 변환관계를 바탕으로 여러 기하학적 문제를 풀게 됩니다.
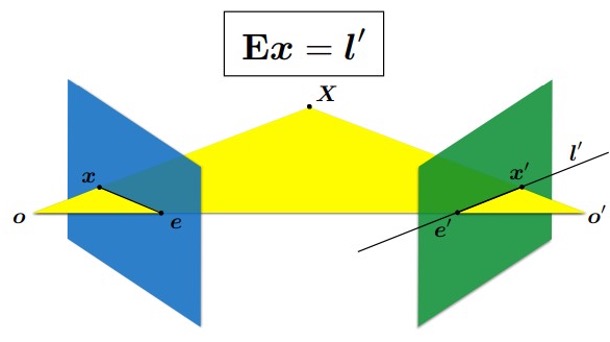
주어진 점 x에 Essential matrix라는 것을 곱하므로써 epipolar line을 얻을 수 있다
Ex = l'
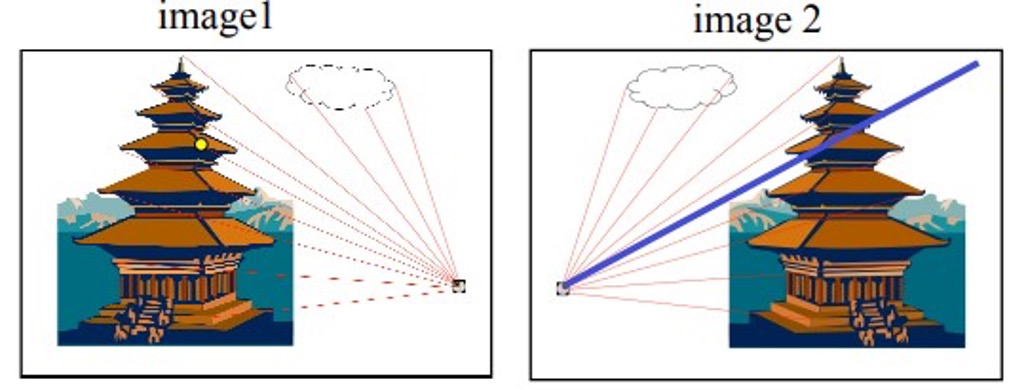
Essential Matrix
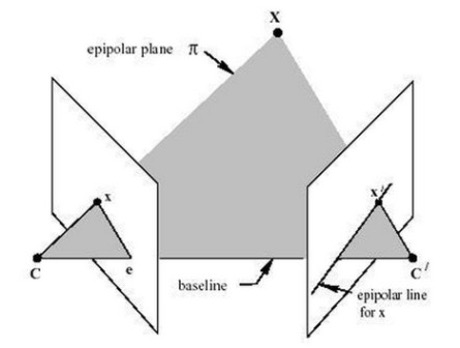
3D 공간상의 한 점 P가 영상 A에서는 p에 투영되고, 영상 B에서는 p'에 투영됐다고 하면 두 영상 좌표 p와 p' 사이에는 다음 관계를 만족하는 행렬이 항상 존재한다는 것이 epipolar geometry의 핵심입니다 (단, p, p'은 normalized 이미지 평면에서의 homogeneous 좌표임).
(1)

(2)
즉, 임의의 두 지점에서 찍은 영상의 매칭점들은 항상 식 (1)을 통해 관계지을 수 있으며, 이 때 식 (1)을 epipolar constraint (또는 essential constraint), 이 3×3 행렬 E를 Essential Matrix라 부릅니다.
Essential Matrix E가 항상 존재하는 이유는 다음과 같습니다. 임의의 두 카메라 좌표축 사이의 관계는 회전, 평행이동에 의해 관계지을 수 있기 때문에 두 카메라 좌표축 사이의 3 × 3 회전행렬을 R, 3 × 1 평행이동 벡터를 t라 했을 때, 외부 공간상의 한 점을 두 카메라 좌표계에서 봤을 때의 관계를
(3)
와 같이 잡을 수 있습니다 (단, P는 외부 공간 상의 점을 A 카메라 좌표계에서 봤을 때의 3차원 좌표, P'은 B 카메라 좌표계에서 봤을 때의 3차원 좌표).
이 때, essential matrix E를 다음과 같이 잡으면
(4)
아래의 식 (5)가 만족됨을 알 수 있습니다. 단, 식 (4)에서 [t]x는 벡터 t와의 벡터 외적(outer product)을 의미합니다. 또한, [t]xR은 t와 R과의 외적을 의미하는게 아니라 먼저 R로 회전을 시킨 후 다음에 t와 외적을 시키는 일련의 변환을 의미합니다. 즉, Ep = [t]xRp = t × (Rp) 입니다.
(5)
(6)
식 (5)의 좌변에 E = [t]xR을 대입해 보면 다음과 같이 항상 0이 나옴을 알 수 있습니다.
(7)
이제 식 (5)의 카메라 좌표를 정규 이미지 좌표로 바꾸면 식 (1)이 성립함을 알 수 있습니다.
(8)
Fundamental Matrix
앞서 설명한 Essential Matrix는 정규화된 이미지 평면에서의 매칭 쌍들 사이의 기하학적 관계를 설명하는 행렬입니다. 즉, 카메라 내부 파라미터 행렬인 K가 제거된 좌표계에서의 변환관계입니다.
반면 fundamental matrix는 카메라 파라미터까지 포함한 두 이미지의 실제 픽셀(pixel) 좌표 사이의 기하학적 관계를 표현하는 행렬입니다.
임의의 두 이미지 A, B에 대하여, 매칭되는 픽셀 좌표 pimg, pimg' 사이에는 항상 다음과 같은 관계를 만족하는 행렬 F가 존재하고, 이러한 행렬 F를 fundamental matrix라 부릅니다.
(9)
(10)
이 때, 이미지 A에 대한 카메라 내부 파라미터 행렬을 K, 이미지 B에 대한 카메라 행렬을 K', 이미지 A, B 사이의 essential matrix를 E라 하면 fundamental matrix F는 다음과 같이 주어집니다.
(11)
(12)
만일 이미지 A, B를 동일한 카메라로 촬영했다면 카메라 행렬(K)이 동일하기 때문에 식 (11), 식 (12)는 다음과 같이 좀더 단순화됩니다.
(13)
(14)
[부연설명]
이미지 픽셀좌표 pimg와 normalized 좌표 p 사이에는 camera matrix K에 대해 다음과 같은 변환관계를 가집니다.
(15)
(16)
따라서 이미지 A의 카메라 파라미터 행렬을 K, 이미지 B의 카메라 파라미터 행렬을 K'라 놓으면 다음 관계가 성립합니다.
(17)
이제 식 (17)를 식 (1)에 대입하면 다음과 같이 fundamental matrix가 구해짐을(존재함을) 알 수 있습니다.
(18)