
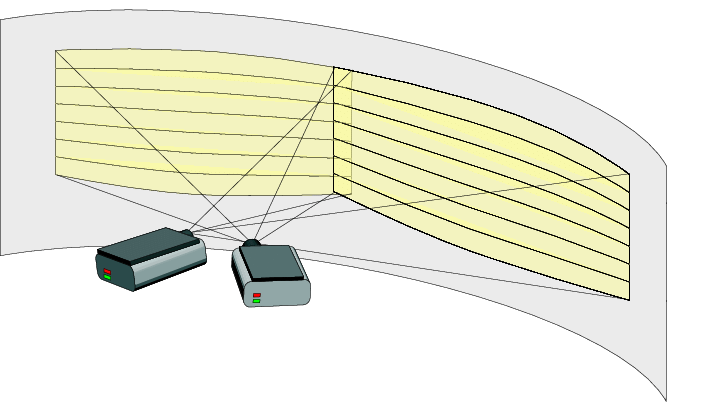
Concept 1
카메라를 원형(팔각형)으로 설치하고 -> 이미지 스티칭 및 블랜딩 -> 그거 자체로 원기둥 이미지의 효과
Concept 2
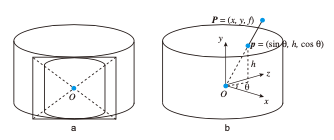
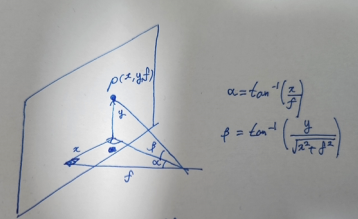
기존의 원통 및 구면 파노라마 영상을 생성하는 방법 에는 전제 조건이 있는데, 카메라가 동일한 높이에서 좌우로 영상을 찍어야만 하며 초점거리 f 값을 알아야한다.
초점거리 f 값이 주어졌을 때 일반적으로 2차원 공간상영상의 모든 점 p=(x, y)의 좌표를 3차원 공간 상의 p=(x, y, f) 점으로 보고 직교(Cartesain) 좌표계 에서 구면 좌표계로 수식 (8)과 같이 변환한다.
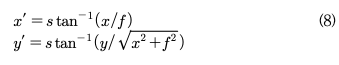
여기서 f는 초점거리, s는 scaling factor 값인데 보통 f와 같은 값을 갖는다. 구면 좌표계로 변환된 (x',y') 값을 다시 수식 (9)과 같이 직교 좌표계 (x",y")로 역 변환하여 구면 영상을 얻는다.
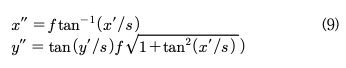

(a)와 같은 영상을 초점거리 f=700으로 가정하여 수식 (8)로 변환시키면 직교 좌표계의 영상을 구면 좌표계상에서 보는 것이 되므로 (b)와 같이 영상의 양 옆 부분은 커지고 더 가까워져 보이게 된다. 수식(9)로 역변환을 시키면 구면 좌표계상에서 보던 영상을 다시 직교 좌표계로 가져오는 것이 되며 (c)와 같이 된다. 이때 모든 수평선들은 곡선 을 이루게 된다.
일반적인 구면 파노마라 영상 생성 방법은 이와 같이 먼저 모든 영상에 대해서 구면 영상 변환을 수행하고 x, y축으로의 이동(t_x, t_y) 두 개의 매개변수만으로 매 칭을 하여 합성한다. 이때 사용자는 고정된 높이의 카 메라를 통해 어떠한 회전이나 스케일 변화 없이 좌우상 하이동만으로 영상을 찍어야 한다. 이동 외의 회전 및 스케일 변화가 생기면 영상 매칭이 어려워지고 정보 손실이 더 커질 수 밖에 없으며 사용자가 카메라를 손에 쥐고 있으면 회전이나 스케일의 변화를 안주고 x, y축 으로만 돌려 촬영한다는 보장은 없다.
사용자에 의해 생길 수 있는 여러 변화에 강건한 구면 파노라마 영상 생성하는 방법 즉, 어떤 카메라든 상관없이 동영상을 촬영한 후 손 흔들림으로 인한 회전, 스케일의 변화가 있더라도 효과적으로 구면 파노라마 단일 영상을 생성하는 방법을 제안한다.
먼저 모든 프레임에 대해서 영상을 호모그래피로 변 환한 후, 단일 영상을 얻었을 때 수식 (9)의 구면 좌표계 역변환을 한번만 수행하여 구면 파 노라마 영상을 얻는 방법을 제안한다. 평면 파노마라 영상은 자유도가 8인 호모그래피로 합성되기 때문에 이동, 회전, 스케일, 원근 변화에서도 최적의 변환을 수 행할 수 있어서 기존의 원통 및 구면 파노라마 영상에 비해 정보 손실이 작은 편이다. 기존의 구면 파노라마 영상 생성 방법과 달리 각 영상에 대해서 먼저 구면 영상 변환을 하지 않고 호모그래피를 통해 평면 파노라마 영상을 얻은 후에 초점거리 정보를 이용해 구면 좌표계 역변환 수식 (9)로 한번 변환시켜 원하는 구면 파노라 마 영상을 생성하는 방법이다. 여기서 수식 (9)의 구면 좌표계 역변환만을 하는 것은 일반 영상과 다르게 평면 파노라마 영상에 구면 좌표계상에서 보는 것과 같은 원근 정보가 포함되어 있기 때문이다. 카메라의 초점거리 정보를 모르는 상태에서는 호모 그래피 행렬 매개변수들을 이용해 이를 계산할 수 있 다. 각 호모그래피는 수식 (10)와 같이 표현될 수 있다.
여기서 K0, K1은 두 영상에 대한 초점거리와 중심점 매 개변수를 갖는 카메라 내부(intrinsic)행렬, R는 회전 매개변수들을 갖는 외부(extrinsic)행렬이며 간단한 연산을 통해 초점거리 f0, f1을 쉽게 구할 수 있다. 추 정된 두 개의 초점거리 f0, f1의 기하학적 평균을 최종 초점거리 f로 택한다. 예시에서는 모든 호모그래피 에서 초점거리를 각각 계산하고 중간(Median)값을 최종적으로 선택하였다.

Concept 3
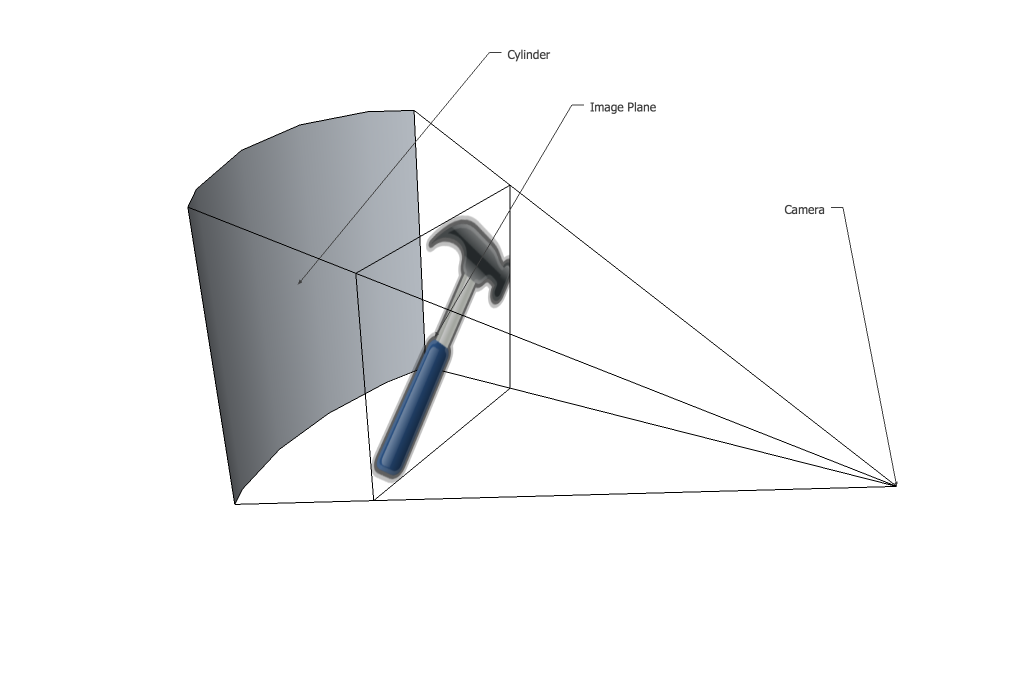
오목한 원통이 앞에 있는 평면 이미지가 있다고 가정
첫 번쨰 단계는, 이미지를 곡면으로 직교 투영을 수행하는 것입니다.
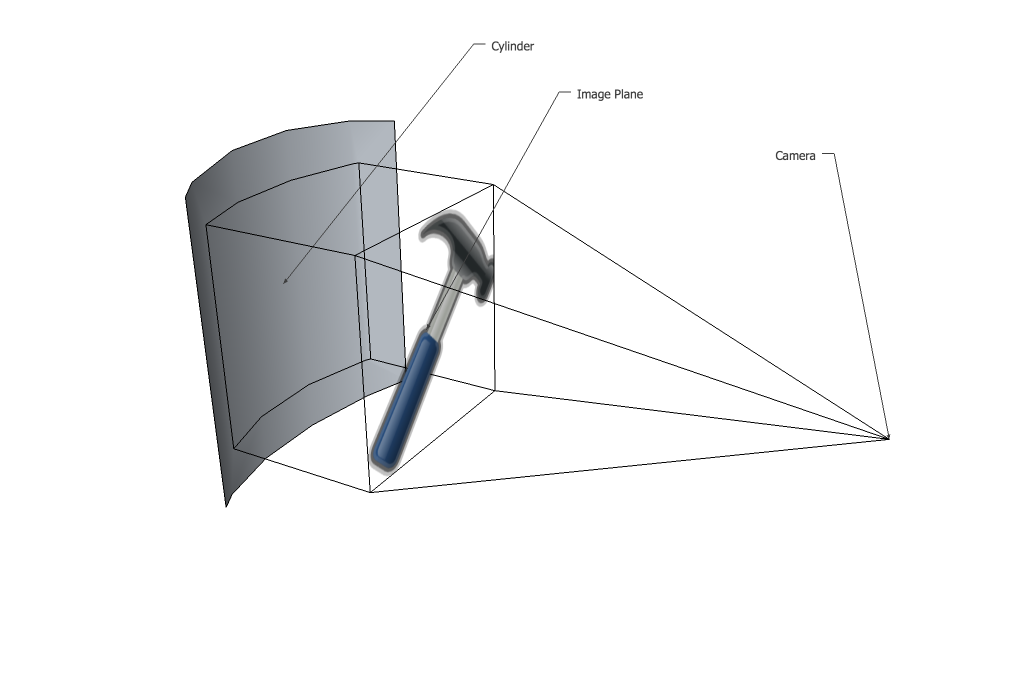
그런 다음 해당 점은 이미지 평면에 다시 원근법으로 투영됩니다. 이 경우 실린더의 모든 부분이 이미지 평면보다 큰 z 좌표를 가지기 때문에 전체 이미지가 축소됩니다. 귀하의 경우 실린더가 왼쪽 및 오른쪽 가장자리의 이미지 평면에 닿아 축소가 발생하지 않습니다. 포인트가 다시 투영되면 이미지 평면에서 더 이상 평평한 선을 형성하지 않으며 x에 따라 달라지는 원통의 z 좌표 때문에 곡선이 있습니다.
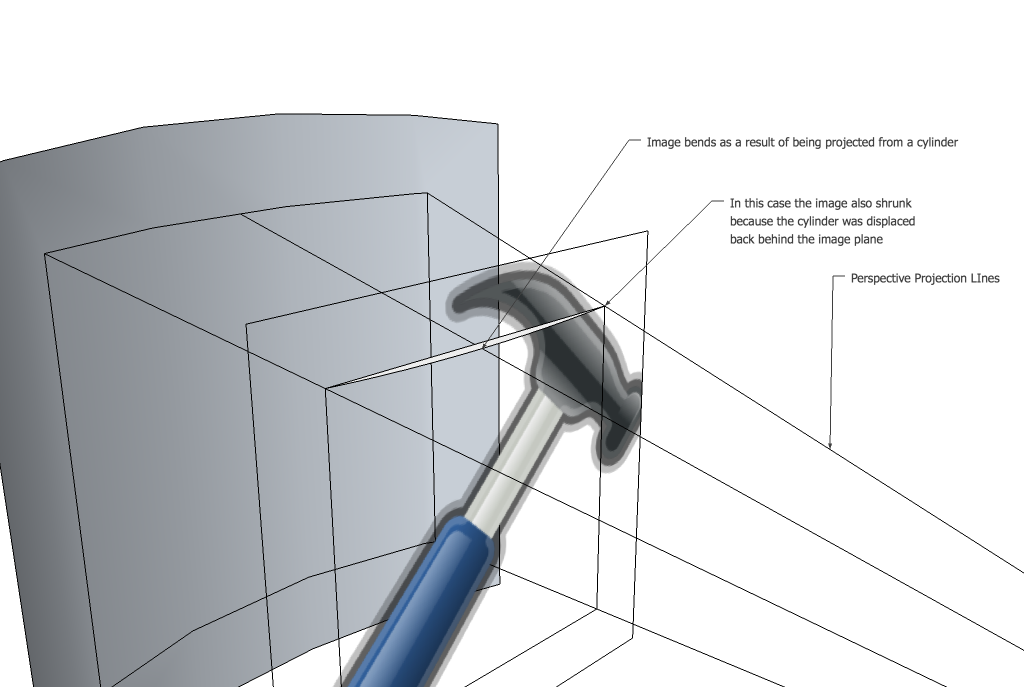
첫 번째 트릭은 실제로 이 프로세스를 거꾸로 표현하려는 것입니다. 먼저 원본 이미지의 모든 픽셀을 가져와 새 이미지로 옮기고 싶다고 생각할 수 있습니다. 이전 이미지에 나타난 새 이미지의 모든 픽셀을 확인하고 색상을 설정하면 실제로 훨씬 더 잘 작동합니다. 즉, 3가지 작업을 수행해야 합니다.
- 실린더 매개변수 설정
- 카메라에서 광선을 투사하여 새 이미지의 각 지점을 통과하고 실린더에서 x,y,z 좌표를 찾습니다.
- 직교 투영을 사용하여 해당 광선을 이미지 평면으로 다시 이동합니다(단지 z 구성 요소를 드롭한다는 의미임).
모든 것을 추적하는 것은 약간 까다로울 수 있으므로 일관된 용어를 사용하려고 노력할 것입니다. 우선, 실린더가 가장자리에서 이미지에 닿도록 보장하고 싶다고 가정합니다. 이것이 사실이라면 선택할 수 있는 2개의 자유 매개변수는 실린더 반경과 초점 거리입니다.
zx 평면에서 원의 방정식은 다음과 같습니다.

원의 중심이 z축에 있다고 가정합니다. 실린더의 가장자리가 너비가 w이고 초점 거리가 f인 이미지 평면의 가장자리에 닿을 경우

이제 우리는 카메라에서 xim의 이미지 평면을 통해 xc의 실린더로 라인을 투사하는 2단계로 이동하는 실린더의 모든 매개변수를 알고 있습니다. 다음은 용어의 빠른 다이어그램입니다.
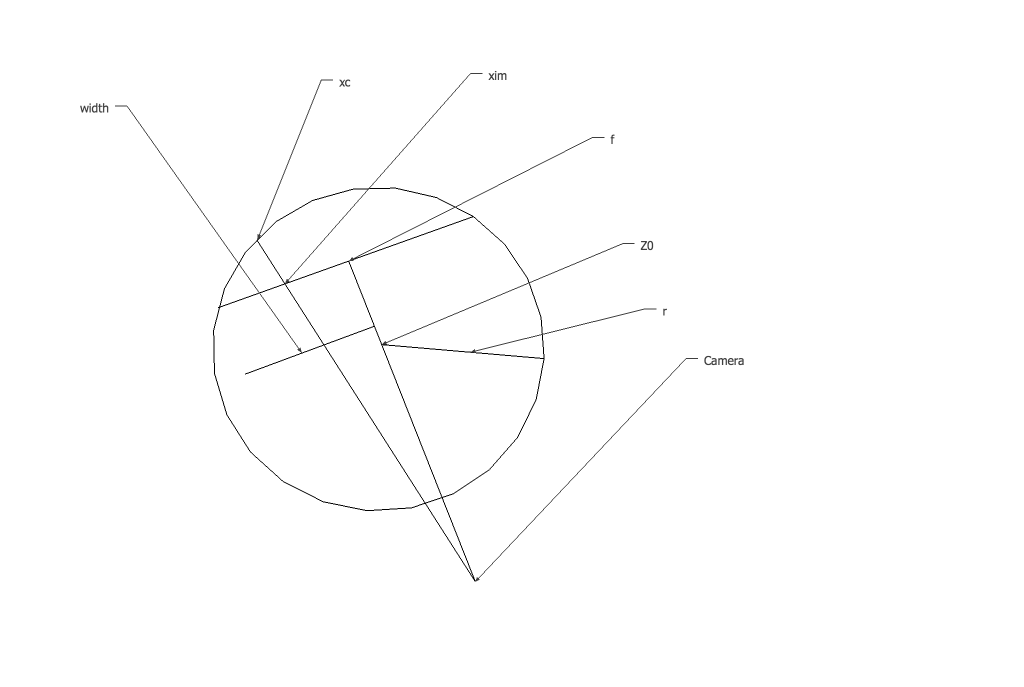
우리가 투사하는 선이 원점에서 시작하여 xim에서 이미지 평면을 가로지르는 것을 알고 있습니다. 방정식을 다음과 같이 쓸 수 있습니다.

원통을 통과할 때 x 좌표를 원하므로 방정식을 결합합니다.

이차방정식을 사용하여 z를 구한 다음 다시 선 방정식에 연결하여 x를 얻을 수 있습니다. 두 솔루션은 선이 원에 닿는 두 위치에 해당합니다. 우리는 이미지 평면 이후에 발생하는 하나에만 관심이 있고 하나는 항상 더 큰 x 좌표를 가지므로 -b + sqrt(...)를 사용하십시오. . 그 다음에
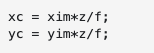
직교 투영을 제거하는 마지막 단계는 간단합니다. z 구성 요소를 놓으면 완료됩니다.
참고링크
https://stackoverflow.com/questions/12017790/warp-image-to-appear-in-cylindrical-projection
http://paulbourke.net/panorama/cylinder
https://chamcham.tistory.com/25
https://www.morethantechnical.com/2018/10/30/cylindrical-image-warping-for-panorama-stitching/

